R语言-生存分析
有关生存分析的相关知识,请自行前往“算法与模型”类博客进行学习。
(http://blog.csdn.net/xiaohukun/article/details/77679134)
一、下载并加载包
进行生存分析使用的是survival 包
install.packages("survival") #安装survival包library(survival) #加载survival包
二、准备数据
使用survival包自带的“pbc”数据集为例(418*20)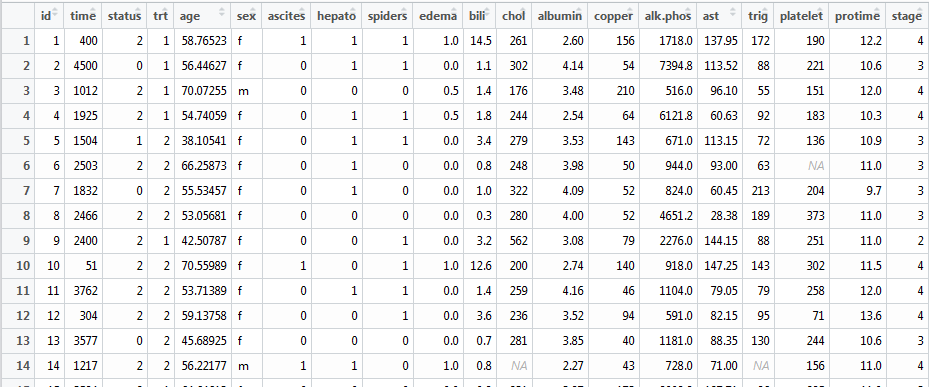
这里记录的time只是原始时间,还需要根据status判断生存时间的类型,转化成相应的格式。这个工作由Surv(time,event)完成,并返回生存对象
> Sur_Obj<-Surv(pbc$time,pbc$status)> Sur_Obj[1] 400 4500? 1012 1925 1504+ 2503 1832? 2466 2400[10] 51 3762 304 3577? 1217 3584 3672? 769 131 ……
三、绘制生存曲线
函数surfit(formula),根据填入的formula按照默认K-M算法进行生存曲线拟合。如果填入的formula只有一个向量,则写成x~1的形式。
#获得曲线模型> model<-survfit(Sur_Obj~1)> summary(model)Call: survfit(formula = Sur_Obj ~ 1)232 observations deleted due to missingnesstime n.risk n.event survival std.err lower 95% CI upper 95% CI41 186 2 0.98925 0.00756 0.97454 1.000043 184 1 0.98387 0.00924 0.96593 1.000051 183 1 0.97849 0.01064 0.95787 0.999671 182 1 0.97312 0.01186 0.95015 0.996677 181 1 0.96774 0.01296 0.94268 0.993594 180 1 0.96237 0.01395 0.93540 0.9901110 179 1 0.95699 0.01488 0.92827 0.9866111 178 1 0.95161 0.01573 0.92127 0.9830130 177 1 0.94624 0.01654 0.91437 0.9792……#其中lower 95% CI 和 upper 95% CI为95%置信度时生存率的上下区间> modelCall: survfit(formula = Sur_Obj ~ 1)232 observations deleted due to missingnessn events median 0.95LCL 0.95UCL186 161 1217 1077 1492#其中median 即为中位生存期,0.95LCL,0.95UCL为预测上下限
直接通过plot(model,ylab = "生存率",xlab="天")便可以绘制生存曲线。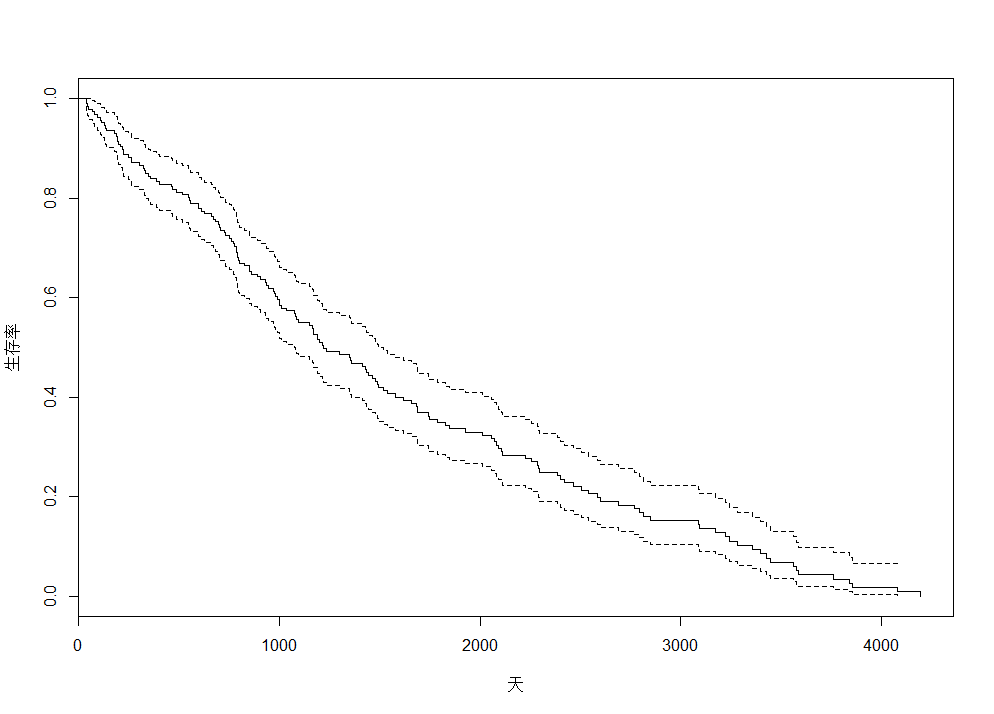
四、单因素分析
这里主要是指用survdiff(formula)函数进行log-rank检验。
> survdiff(Sur_Obj~pbc$trt) #trt是分组条件Call:survdiff(formula = Sur_Obj ~ pbc$trt)n=144, 274 observations deleted due to missingness.N Observed Expected (O-E)^2/E (O-E)^2/Vpbc$trt=1 75 65 65.5 0.00441 0.00956pbc$trt=2 69 60 59.5 0.00486 0.00956Chisq= 0 on 1 degrees of freedom, p= 0.922
原假设为两类数据均值无明显差异,P值为接收原假设的概率,显然此处>>0.05,因此不能拒绝原假设。结论:trt不同的患者生存时间并无明显差异。
五、多因素分析
采用逐步回归的方式一步一步确定影响因素是否进入模型,并进行协变量的PH假定验证。分别使用到coxph(formula)函数和cox.zph(fit)函数。
#相似比检验,原假设为加入新因素无差别,P值看是否为影响因素,coef为系数> coxmodel<-coxph(Sur_Obj~pbc$bili)> coxmodelCall:coxph(formula = Sur_Obj ~ pbc$bili)coef exp(coef) se(coef) z ppbc$bili 0.078 1.081 0.013 6.01 1.8e-09Likelihood ratio test=28.6 on 1 df, p=9.09e-08n= 186, number of events= 161(232 observations deleted due to missingness)#原假设为符合PH假定> zphmodel<-cox.zph(coxmodel)> zphmodelrho chisq ppbc$bili 0.00717 0.0064 0.936
也可以通过绘制β图的方法看系数的变化趋势,如变化不大则也认为符合PH假定。plot(zphmodel)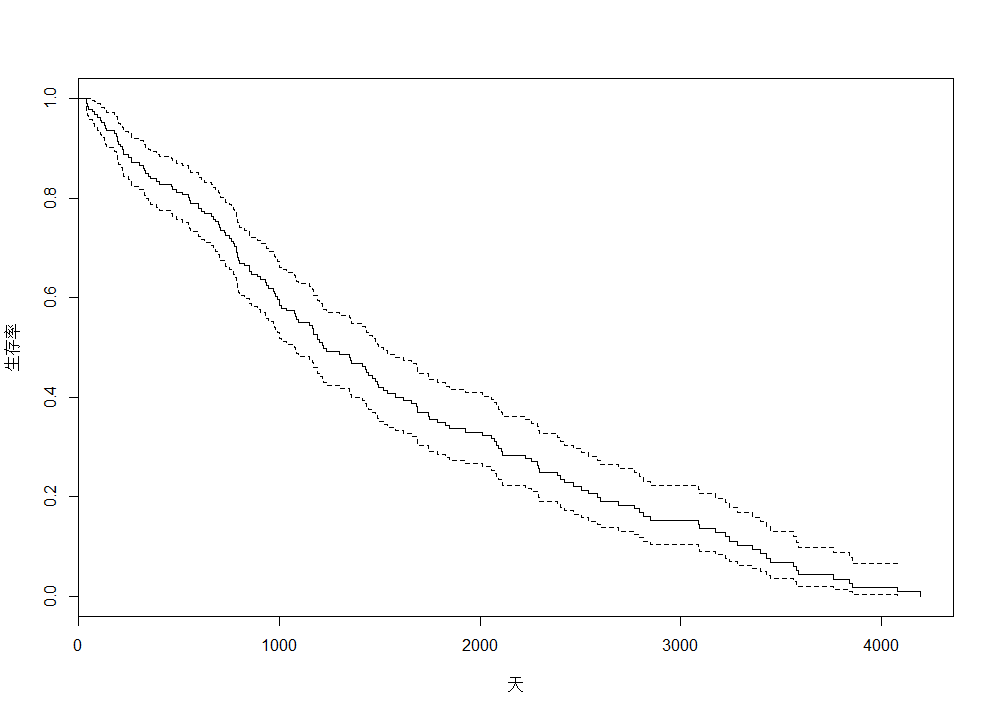
如此,生存分析中涉及的基本分析就完成了。
































还没有评论,来说两句吧...