直方图变换
直方图变
直方图拉伸(Histogram stretching)
图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。
直方图拉伸是通过对比度拉伸对直方图进行调整，从而“扩大”前景和背景灰度的差别，以达到增强对比度的目的，这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。这种方法也叫做归一化。
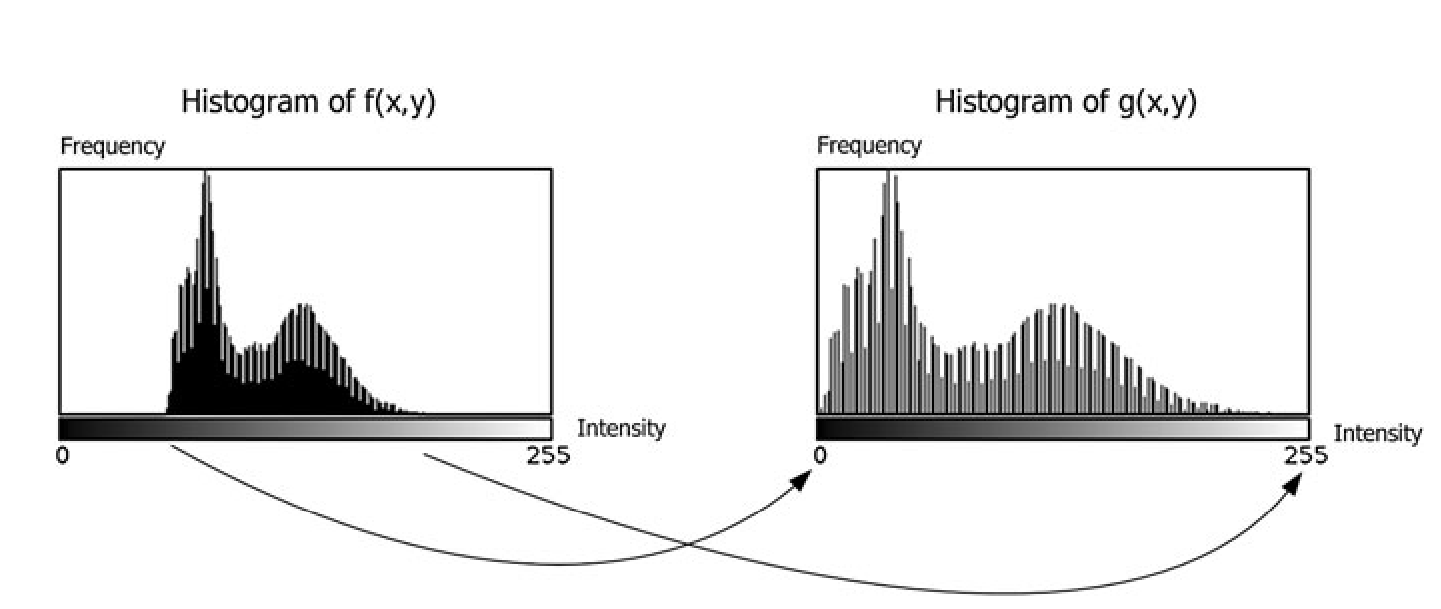
我们将一个灰度范围在[x,y]的图像进行直方图拉伸，使其灰度范围变成[a,b]。那么对于某个像素点的灰度z，变化为z′：
z′=b−ay−x(z−x)+a
效果如下
直方图均衡化(Histogram equalization)
直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
直方图均衡化常用来增强图像全局对比度。但变化后图像灰度级减少，某些细节消失。
步骤：
- 统计每个灰度级的像素个数
- 统计每个像素级的累计像素个数
- 重新计算每个像元灰度值
我们来看一个灰度图像，让ni表示灰度出现的次数，这样图像中灰度为i的像素的出现概率是
px(i)=nin,0≤i≤L
L是图像中所有的灰度数，n是图像中所有的像素数, p实际上是图像的直方图，归一化到[0,1]之间。
设c为p的累计概率函数(cumulative distribution function)，定义如下：
c(i)=∑j=0ipx(j)
c是原图像的归一化累计直方图。
我们创建一个形式为y=T(x)的变化，对于原图像中的每个灰度值，它就产生一个y，这样的y的累计概率函数就可以再所有范围进行线性变化，转化公式定义为：
yi=T(xi)=c(i)
注意T将不同的登记映射到[0,1]，为了将这些值映射回最初的域，则需要一定地改变：
y′i=yi×(max−min)+min
其中max和min是图像灰度值的上下界。
效果如下
ゝ一纸荒年。
红太狼
太过爱你忘了你带给我的痛
还没有评论，来说两句吧...