vtk实现三点确定一个平面-蒲公英云

如何在vtk中根据三点提取一个切面，一直知道根据三点就能表示一个面，但是怎么在vtk中实现，对于我这种菜鸟真是要想好久。首先说说现在的思路，知道vtkImagepalne中可以根据一个点和一个面法向量获得一个面。现在我有三个点，需要获得一个面法向量，那么需要通过叉乘得到，再然后根据一个点和得到的面法向量显示一个切面。

之前看过vtkresliceImage得到的切面方法，感觉对变换的理解很差，尤其对Matrix（矩阵基本变换）的理解又不那么到位：
double center[3]; center[0] = origin[0] + spacing[0] * 0.5 * (extent[0] + extent[1]); center[1] = origin[1] + spacing[1] * 0.5 * (extent[2] + extent[3]); center[2] = origin[2] + spacing[2] * 0.5 * (extent[4] + extent[5])； static double axialElements[16] = { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }; vtkSmartPointer<vtkMatrix4x4> resliceAxes = vtkSmartPointer<vtkMatrix4x4>::New(); resliceAxes->DeepCopy(axialElements); resliceAxes->SetElement(0, 3, center[0]); resliceAxes->SetElement(1, 3, center[1]); resliceAxes->SetElement(2, 3, center[2]);
根据代码的理解，vtkMatrix4x4应该包含一个面和一个点，但是这个面是由static double axialElements[16] = { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 };
决定的，根据定义，这个矩阵左上方3x3的矩阵是X、Y、Z方向的三个矢量，第四列三个做透视变换用的，根据水灵书中提的，这里好像是切面的坐标系原点（我没有看过透视变换的相关信息，不太了解）。第四行左三个别控制其在x轴y轴z轴上的平移单位.，第四个表示缩放比例。

再理解一下叉乘，叉乘（cross product）或者外积，它的计算结果是一个向量而非标量。叉积所在的向量与参与运算的两个向量都正交，也即正交于原来的两个向两边所决定的平面，也即两向量所决定的平面的法向量可通过计算叉积的方式得以确定。当参与运算的两向量是平行的两个向量时，得到的叉积为0，也即可通过计算叉积的方式判断两向量是否平行。
代数定义
二维时
x×y=x1y2−x2y1
三维时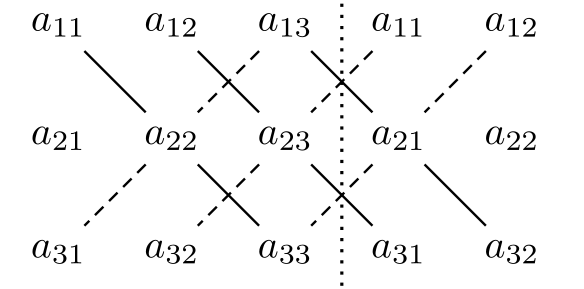
这里写图片描述

这里写图片描述
根据如图的计算方法可得：

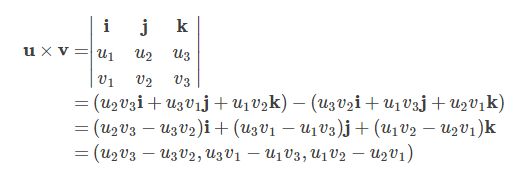
这里写图片描述
几何定义

x×y=∥x∥∥y∥sinθn⃗
n⃗ 表示叉积方向上的单位向量。

中学知识告诉我们三角形的面积计算公式为：

S=∥x∥∥y∥sinθ2=∥z∥h2

其中θ表示的是x,y之间的夹角，由以上两个公式我们可得到三角形的高或者点到其所对的边的距离，也即点到直线的距离，的计算公式：
h=∥x×y∥/∥z∥

double operator*(const Vec& x, const Vec& y)
{
    assert(x.size() == y.size());       // #include <cassert>
    double sum = 0.;
    for (size_t i = 0; i < x.size(); ++i)
        sum += x[i]*y[i];
    return sum;
}
// 三维的情况
Vec operator^(const Vec& x, const Vec& y)
{
    assert(x.size() == y.size() && x.size() == 3);
    return Vec{x[1]*y[2]-x[2]*y[1], 
                x[2]*y[0]-x[0]*y[2],
                x[0]*y[1]-x[1]*y[0]};
            // uniform initialization, C++11新特性
}
// 二维就姑且返回其模长吧
double twoDCrossProd(const Vec& x, const Vec& y)
{
    return x[0]*y[1]-x[1]*y[0];
}

现在贴一段代码[C++实现叉乘]，并感谢作者提供。(http://blog.sina.com.cn/s/blog_4e24d9c50100ttvz.html)

#include <iostream>
#define M 3
#define N 4
#define P 3
using namespace std;
void getmt(int* m,int r,int c)              //获取矩阵
{
     for(int i=0;i<r;++i)       
    {
            for(int j=0;j<c;++j) cin>>*(m+i*c+j);
    }
 }
void showmt(const int* m,int r,int c)      //显示矩阵
{
     for(int i=0;i<r;++i)
     {
             for(int j=0;j<c;++j) cout<<*(m+i*c+j)<<"\t";  
             cout<<endl;     
     }
 }
void mmt(const int* m1,const int* m2,int* m3,int m,int n,int p)
{
     for(int i=0;i<m;++i)                 //叉乘运算
    {
        for(int j=0;j<p;++j)
        {
                for(int k=0;k<n;++k)
                {
                        (*(m3+i*p+j))+=(*(m1+i*n+k))*(*(m2+k*p+j));
                 }
        }
    }
 }
int main(int argc, char *argv[])
{
    int m1[M][N];
    int m2[N][P];
    int m3[M][P];
    memset(m3, 0, sizeof(m3));    //注意不能用int m3[M][P]={0};来初始化为0,这样可能并没有将m3中的元素赋0
    cout<<"为矩阵1输入"<<M<<"*"<<N<<"个数："<<endl;
    getmt(&m1[0][0],M,N);        //获取矩阵m1
    cout<<"为矩阵2输入"<<N<<"*"<<P<<"个数："<<endl;
    getmt(&m2[0][0],N,P);        //获取矩阵m2 
    mmt(&m1[0][0],&m2[0][0],&m3[0][0],M,N,P);   //叉乘运算
    cout<<"矩阵1："<<endl;
    showmt(&m1[0][0],M,N);
    cout<<"矩阵2："<<endl;
    showmt(&m2[0][0],N,P);
    cout<<"结果："<<endl;
    showmt(&m3[0][0],M,P);
    system("PAUSE");
    return EXIT_SUCCESS;
}

搜了一下在图形学中表示向量的方法，看来这里面学问挺多的，贴两个实用的帖子，感谢作者提供宝贵的知识图形学中向量操作类、图像学中向量说明。

vtkImagePlaneWidget中不能直接设置SetNormal和SetCenter，只能设置初始点位置，那么这样就需要写一个类来继承vtkImagePlaneWidget，并且添加这两个功能。最后，继承了vtkPlaneSource中SetNormal和SetCenter这两个功能，可以提取经过三个点的切面：

ImagePlaneWidget *mplanewidget = ImagePlaneWidget::New();
    mplanewidget->SetInteractor(iren);
    mplanewidget->SetPicker(picker); //定义 内部选择器
    mplanewidget->SetTexturePlaneProperty(ipwProp);//给切片设定纹理属性
    mplanewidget->TextureInterpolateOff();   
    mplanewidget->GetPlaneProperty()->SetColor(1, 0, 0); //设置平面属性
    mplanewidget->SetResliceInterpolateToLinear();//差值方法
    mplanewidget->SetInputConnection(reader->GetOutputPort());//
    //mplanewidget->RestrictPlaneToVolumeOn(); //确保平面在容器范围之内
    mplanewidget->SetNormal(mnormalize);  //设定切面法向方向
    mplanewidget->SetOrigin(moriginpoint); //设定切面的初始点位置
    mplanewidget->SetCenter(moriginpoint);  //设定切面所在位置中心
    mplanewidget->On();
    mplanewidget->InteractionOn();
    //mplanewidget->PlaceWidget(polyData->GetBounds());//获得polydata中的边界，最大最小值