ACM 树的递归 Not so Mobile & The Falling Leaves-蒲公英云

ACM 树的递归 Not so Mobile & The Falling Leaves

滴，集训第一天打卡。

今天是紫书第六章训练+STL的运用。

STL的就不放啦~这里有2道表面是建树，其实是递归（不必要建树）的题讲一下。

（哇，刷新了我对递归的认识..感觉超级厉害的！）

UVA 839 Not so Mobile

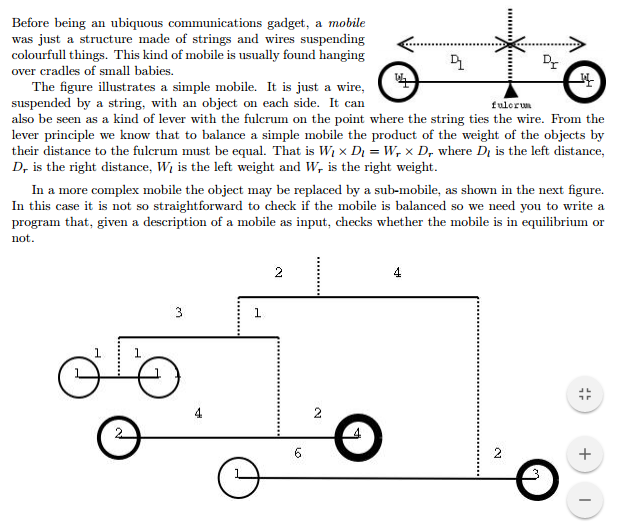
题目大意：给你一个杠杆两端的物体的质量和力臂，如果质量为零，则下面是一个杠杆，判断是否所有杠杆平衡。

#include<iostream>
using namespace std;
bool solve(int& W) 
{
    int W1,D1,W2,D2;
    bool b1=true,b2=true;
    cin>>W1>>D1>>W2>>D2;
    if(!W1) 
    b1=solve(W1);
    if(!W2) 
    b2=solve(W2);
    W=W1+W2;
    return b1&&b2&&(W1*D1==W2*D2);
}
int main() 
{
    int T,W;
    cin>>T;
    while(T--) 
    {
        if(solve(W))
         cout<<"YES"<<endl; 
        else 
        cout<<"NO"<<endl;
        if(T) 
        cout<<endl;
      }
      return 0;
}

UVA 699 The Falling Leaves

题目大意：给定一棵树，从左到右计算竖着的权值合，例如图就是7，5+6，3

#include <iostream>  
#include <cstring>  
using namespace std;  
const int maxNum = 1005;  
int sum[maxNum];  
void build(int pos)   
{// 输入并统计子树，水平位置为pos  
    int v;  
    cin >> v;  
    if(v == -1) return;// 空树结点  
    sum[pos] += v;  
    build(pos - 1);  
    build(pos + 1);  
}  
bool init()   
{// 输入并初始化树根，再构建子树  
    int v;  
    cin >> v;  
    if(v == -1) return false;  
    memset(sum, 0, sizeof(sum));     
    int pos = maxNum / 2; // 树根的水平位置  
    sum[pos] = v;  
    build(pos - 1);// 构建左子树堆  
    build(pos + 1);// 构建右子树堆  
    return true;
}  
int main()   
{  
    int kase=0;  
    while(init())   
    {  
        int p=0;  
        while(sum[p]==0)   
        p++;   
        cout << "Case " << ++kase << ":\n" << sum[p++];  
        while(sum[p]!= 0)    
        cout << " " << sum[p++];  
        cout << "\n\n";  
    }  
    return 0;
}

再贴一个学姐的代码~

#include<stdio.h>
#include<string.h>
int a[200];
void f(int y)
{
    int x;
    scanf("%d",&x);
    if(x==-1)return;
    a[y]+=x;
    f(y-1),f(y+1);
}
int main()
{
    int n,k,x,l=0,i;
    while(scanf("%d",&x),x!=-1)
    {
        k=0;
        memset(a,0,sizeof(a));
        a[100]=x;
        f(99),f(101);
        printf("Case %d:\n",++l);
        for(i=0;i<200;i++)
        {
            if(a[i]!=0)
            {
                if(k)printf(" ");
                printf("%d",a[i]);
                k=1;
            }
        }
        puts("\n");
    }    
}