因子分析Factor analysis
简介：本文主要介绍EM算法求解因子分析问题
因子分析Factor analysis
在文章 EM算法 求解混合高斯模型时，通常假设拥有足够多的样本去构造这个混合高斯分布，即样本数量n要远大于样本维数d： 如果样本数量小于样本维数，那么协方差矩阵
是奇异矩阵,那么
和
都无法计算。在因子分析中，一个d维的向量通常由一个k维向量生成，通常k远小于d。具体模型如公式1所示:
公式1
上式中d x k维矩阵 称为因子载荷矩阵factor loading matrix,k维向量z称为因子factors,d维向量
是满足均值为0，对角协方差矩阵的高斯分布的噪声，那么根据公式1该模型写成概率形式如公式2所示：
公式2
该模型如图1所示：
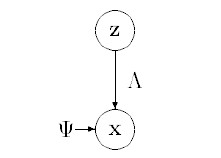
图1 因子分析生成模型
根据 Pattern Recognition and Machine Learning 已知公式2可得x的边缘概率和已知z的条件概率如公式3和公式4所示(详见原书公式2.113-2.117):
公式3
公式4
根据公式3采用极大似然估计法maximum-likelihood estimation (MLE) 可以的到似然函数如公式5所示：
公式5
直接对公式5求导并令其等于0很难得到结果，而EM算法可以很好的解决这个问题。
回顾 EM算法 (这里z为隐含变量)，迭代过程如下所示：
- E-Step:
公式6
- M-Step:
公式7
上述算法E-Step直接利用公式4的结论，下面详细分析M-Step。把要求的最大化概率推到导公式8所示，其中K是和参数无关的常量：
公式8
去掉常量，最终需要最大化的式子如公式9所示：
公式9
- 求参数
根据矩阵迹Trace性质 和矩阵求导的性质
,公式9对
求偏导如下：
公式10
带颜色部分利用了矩阵相关性质,令其等于0我们可以得到：
整理可得 如公式11所示：
公式11
根据公式4，E[z]如公式12所示：
公式12
根据公式4，E[zz’]如公式13所示：
公式13
- 求参数
公式9对 求偏导如下：
公式14
最后一步通过公式11代入得到，那么整理得到：
加上对角限制最终表达式如公式15所示：
公式15
EM算法运用于因子分析过程如下所示：
- E-Step:
- M-Step:
至此关于因子分析和EM算法推到全部结束。
参考文献
1、 CS229 Factor analysis
2、 The EM Algorithm for Mixtures of Factor Analysis
3、 The Expectation-Maximization (EM) Algorithm
4、 Pattern Recognition and Machine Learning
柔光的暖阳◎
朱雀
小灰灰
分手后的思念是犯贱
傷城~
向右看齐
迷南。
还没有评论，来说两句吧...