线段树区间更新

淩亂°似流年 2022-08-03 16:38 357阅读 0赞

线段树成段更新延迟标记理解

区间更新是指每次更新的时候更新的是一个区间里面的所有值，例如将区间[l,r]内的所有点都加或者减去一个数，或者替换成一个数字等等.因为区间更新每次更新的不止一个叶子节点，而叶子节点的值的更新肯定会影响到他的一系列的节点，所以假如每次都按照单点更新的思路将每一个叶子节点以及他的父节点都更新的话，那么工作量太大了并且时间肯定不会是log(n)会超时的。例如线段树总区间为[1,10]，也就是这个树：

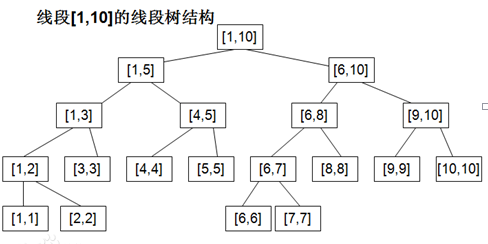
Center

现在我们要更新[4,8]内的叶子节点的值，那么总共要更新的节点就会非常多。为了解决这个可能会超时的做法，引入了线段树中的延迟标记，这也是线段树的精华部分。延迟标记：每个节点除了常规的lft，rht，value外在增加一个标记，这个标记用于记录这个节点是否进行了某种修改(这种修改操作会影响其子节点)，对于任意区间的修改，我们先按照区间查询的方式将其划分成线段树中的节点，然后修改这些节点的信息，并给这些节点标记上代表这种修改操作的标记。在修改和查询的时候，如果我们到了一个节点p，并且决定考虑其子节点，那么我们就要看节点p是否被标记，如果有，就要按照标记修改其子节点的信息，并且给子节点都标上相同的标记，同时消掉节点p的标记。这样一来成段更新的时候每次只需要更新有用的部分就可以了。

举例说明：当我们要将区间[1,3]的叶子节点的value增加2的时候，我们利用和区间查询一样的办法找到了区间[1,3]，这时候我们把区间[1.3]的value值加上区间长度len\2，然后把他的延迟标记记为2，这时候这一次的区间更新就完成了，不需要更新[1,3]的子节点。当我们然后继续要将区间[3,5]内的叶子节点value增加2，这时候查询到[1,3]的时候我们发现要用到他的字区间[3,3]并且[1,3]已经被标记了，这时候我们就要把[1,3]的标记向子节点传递，分别将他的字节点区间[1,2]的标记都记为2然后区间的value值加上区间长度len**2（父区间的标记值）,然后将区间[1,3]的标记清0，然后将区间[4,5]按上面的方法更新一下就可以了。当区间更新的区间长度为1的时候就是单点更新，单点更新只是区间更新的特例。

-hdu 1698 Just a Hook（成段更新）

-题意：有t组测试数据，n为钩子长度（1<=n<=100000）,m为操作的次数。初始时，每个钩子的价值为1，操作由三个数字组成x,y,z表示把区间[x,y]的钩子变成的价值变成z（1代表铜，2银，3金）,最后求钩子的总长度。

思路：线段树的成段更新问题，重点是使用了延迟标记type，即每次成段更新的时候，类似与询问query函数，只更新到包含该区间的最大区间就可以了。

上面有详细讲解。也可以看代码注释。

  1. #include <iostream>
  2. #include <cstdio>
  3. #include <cstring>
  4. #include <cmath>
  5. #include <algorithm>
  6. #include <queue>
  7. #include <stack>
  8. using namespace std;
  10. int n,m;
  11. const int maxn = 100005;
  13. struct node
  14. {
  15.     int lft,rht;
  16.     int value,type;
  17.     //flag为延迟标记符
  18.     void fun(int temp)
  19.     {
  20.         type=temp;
  21.         value=(rht-lft+1)*type;//直接将alue的值更改
  22.         //有时候是需要累加的，或者累减的
  23.     }
  24. }tree[maxn<<2];
  26. void rest(int ind)
  27. {
  28.     //延迟操作
  29.     if(tree[ind].type)
  30.     {
  31.         tree[ind*2].fun(tree[ind].type);
  32.         //将节点ind的延迟标记type以及value传向儿子节点
  33.         tree[ind*2+1].fun(tree[ind].type);
  34.         tree[ind].type=0;//将该节点的延迟标记清0
  35.     }
  36. }
  38. void build(int lft,int rht,int ind)
  39. {
  40.     tree[ind].lft=lft;
  41.     tree[ind].rht=rht;
  42.     tree[ind].value=rht-lft+1;//初始叶子节点的值都为1
  43.     tree[ind].type=0; //初始延迟标记，tree[ind].type=1也可以
  44.     if(lft!=rht)
  45.     {
  46.         int mid = (tree[ind].lft+tree[ind].rht)/2;
  47.         build(lft,mid,ind*2);
  48.         build(mid+1,rht,ind*2+1);
  49.     }
  50. }
  52. void updata(int st,int en,int ind,int type)
  53. {
  54.     //参数多了一个，既是要操作的数字也起到延迟标记的作用
  55.     int lft=tree[ind].lft;
  56.     int rht=tree[ind].rht;
  57.     if(st<=lft&&rht<=en)tree[ind].fun(type);
  58.     //赋值type的同时更新alue的值
  59.     else
  60.     {
  61.         rest(ind);
  62.         //判断节点ind是否有延迟标记,有的话向下操作
  63.         int mid = (tree[ind].lft+tree[ind].rht)/2;
  64.         if(st<=mid)updata(st,en,ind*2,type);
  65.         if(en>mid)updata(st,en,ind*2+1,type);
  66.         tree[ind].value=tree[ind*2].value+tree[ind*2+1].value;
  67.     }
  68. }
  70. int main()
  71. {
  72.     int t,count=1;
  73.     scanf("%d",&t);
  74.     while(t--)
  75.     {
  76.         scanf("%d%d",&n,&m);
  77.         build(1,n,1);
  78.         //cout<<tree[1].value<<endl;
  79.         int a,b,c;
  80.         while(m--)
  81.         {
  82.             scanf("%d%d%d",&a,&b,&c);
  83.             updata(a,b,1,c);
  84.             //cout<<tree[1].value<<endl;
  85.         }
  86.         printf("Case %d: The total value of the hook is %d.\n",count++,tree[1].value);
  87.         //tree[1].value是区间内所有值的和
  88.     }
  89.     return 0;
  90. }

-POJ 3468 A Simple Problem with Integers（成段更新）

题意：题目给你n个数,m个操作，接下来一行给你这n个数，接下的几行给出m个操作，Q a b 表示查询区间[a,b]里的数和和。U a b c 表示把区间[a,b]里的数都加上c。

同样使用延迟标记add。当add不等于0的时候，表示它以下所有区间都需要更新。因为我们没有去改变原始查询区间的区间端点，所以当找到一个区间小于等于查询区间的时候，标记它的延迟标记，返回。注意，因为有可能多次对同一个区间更新值，如果我们直接把标记add=增加值，就不能反应这种情况，所以是add+=增加值，还有，延迟标记也会超int。

  1. #include <iostream>
  2. #include <cstdio>
  3. #include <cstring>
  4. using namespace std;
  6. #define LL(x) (x<<1)
  7. #define RR(x) (x<<1|1)
  8. #define MID(a,b) (a+((b-a)>>1))
  9. const int N=100005;
  10. typedef long long LL;
  12. struct node
  13. {
  14.     int lft,rht;
  15.     LL sum,add;
  16.     int mid(){return MID(lft,rht);}
  17.     void fun(LL tmp)
  18.     {
  19.         add+=tmp;
  20.         sum+=(rht-lft+1)*tmp;
  21.     }
  22. };
  24. int y[N];
  26. struct Segtree
  27. {
  28.     node tree[N*4];
  29.     void relax(int ind)
  30.     {
  31.         if(tree[ind].add)
  32.         {
  33.             tree[LL(ind)].fun(tree[ind].add);
  34.             tree[RR(ind)].fun(tree[ind].add);
  35.             tree[ind].add=0;
  36.         }
  37.     }
  38.     void build(int lft,int rht,int ind)
  39.     {
  40.         tree[ind].lft=lft;    tree[ind].rht=rht;
  41.         tree[ind].sum=0;    tree[ind].add=0;
  42.         if(lft==rht) tree[ind].sum=y[lft];
  43.         else
  44.         {
  45.             int mid=tree[ind].mid();
  46.             build(lft,mid,LL(ind));
  47.             build(mid+1,rht,RR(ind));
  48.             tree[ind].sum=tree[LL(ind)].sum+tree[RR(ind)].sum;
  49.         }
  50.     }
  51.     void updata(int st,int ed,int ind,int add)
  52.     {
  53.         int lft=tree[ind].lft,rht=tree[ind].rht;
  54.         if(st<=lft&&rht<=ed) tree[ind].fun(add);
  55.         else
  56.         {
  57.             relax(ind);
  58.             int mid=tree[ind].mid();
  59.             if(st<=mid) updata(st,ed,LL(ind),add);
  60.             if(ed> mid) updata(st,ed,RR(ind),add);
  61.             tree[ind].sum=tree[LL(ind)].sum+tree[RR(ind)].sum;
  62.         }
  63.     }
  64.     LL query(int st,int ed,int ind)
  65.     {
  66.         int lft=tree[ind].lft,rht=tree[ind].rht;
  67.         if(st<=lft&&rht<=ed) return tree[ind].sum;
  68.         else
  69.         {
  70.             relax(ind);
  71.             int mid=tree[ind].mid();
  72.             LL sum1=0,sum2=0;
  73.             if(st<=mid) sum1=query(st,ed,LL(ind));
  74.             if(ed> mid) sum2=query(st,ed,RR(ind));
  75.             return sum1+sum2;
  76.         }
  77.     }
  78. }seg;
  79. int main()
  80. {
  81.     int n,m;
  82.     while(scanf("%d%d",&n,&m)!=EOF)
  83.     {
  84.         char str[5];
  85.         int a,b,c;
  87.         for(int i=1;i<=n;i++) scanf("%d",&y[i]);
  88.         seg.build(1,n,1);
  89.         while(m--)
  90.         {
  91.             scanf("%s",str);
  92.             if(str[0]=='Q')
  93.             {
  94.                 scanf("%d%d",&a,&b);
  95.                 printf("%lld\n",seg.query(a,b,1));
  96.             }
  97.             else
  98.             {
  99.                 scanf("%d%d%d",&a,&b,&c);
  100.                 seg.updata(a,b,1,c);
  101.             }
  102.         }
  103.     }
  104.     return 0;
  105. }
  111. /*
  112. 题意：对于长度为250000的区间，给了你四种操作：
  113. 操作A，从st到ed这段区间内的数，分别加上1,2,...,st-ed+1。
  114. 操作B，从st到ed这段区间内的数，分别加上，st-ed+1,st-ed,...,1。
  115. 操作C，将st到ed这段区间内的数赋值成x。
  116. 操作S，查询st到ed的这段区间内的数的总和。
  117. */
  119. /*
  120. 对于有多种操作的区间更新线段树，首先是每种操作都要有自己的
  121. 延迟标记符，其次是要弄清楚不同操作之间的顺序性以及联系等。
  122. 比喻说这道题目，操作AB都是加一个等差数列可以看作是一个操作，
  123. 操作C是将区间的值改为另一个数字，这两个操作同时要有延迟标记符。
  124. 但是我们会注意到，当两个操作同时进行时，也就是一个区间这两种
  125. 标记都有的时候，我们怎么向子区间传递呢。应该先传递操作C然后在
  126. 传递操作AB。为什么呢，因为假如后传递C的话那他就会将AB的延迟
  127. 标记符抹掉。或者我们考虑怎么样一个区间才可能同时出现两种标记符呢。
  128. 肯定是先进行了C操作然后在进行AB操作的，因为C操作会将AB操作覆盖。
  129. */
  131. /*
  132. 具体到这道题目，我们发现操作C比较简单常见，在这里就不多叙述。
  133. 我们下面重点看看操作AB，AB操作都是等差数列，所以可以一起进行。
  134. 对于操作AB，我们需要用到三个延迟标记符。
  135. 在线段树的结点中记录了左端点要加的值add1，
  136. 右端点要加的值add2，同时记录了这段区间内的公差step。
  137. 容易得到，等差数列相加还是等差数列，所以可以对一个区间进行多次的AB操作。
  139. 易错点：向子区间传递延时标记的时候，即add1和add2的时候，要分解成两个区间，
  140. 设为(add1,mid1)，(mid2,add2)，通过(add1+add2)/2直接得到mid1，
  141. 然后mid2再根据是递增或是递减相应的加一减一，这里的mid是错误的。
  142. 实际上这里应该只有一个mid，(add1+add2+step)/2，
  143. 这也是为什么在线段树的结点里添加公差step的原因。
  145. */
  147. #include <iostream>
  148. #include <cstdio>
  149. #include <cstring>
  151. using namespace std;
  153. const int N=250005;
  154. typedef long long LL;
  156. struct node
  157. {
  158.     bool flag;  //操作C的延时标记
  159.     int left,right;
  160.     LL add1,add2,step;  //操作A和B的标记，不好理解
  161.      //代表的含义分别是左右端点和公差
  162.     LL sum,valu;
  163.     LL mid(){return left+(right-left)/2;}
  164.     LL len(){return right-left+1;}
  165.     void changeAB(LL a,LL b,LL k)
  166.     {
  167.         add1+=a;    add2+=b;    step+=k;
  168.         sum+=(a+b)*len()/2;  //等差数列和
  169.     }
  170.     void changeC(LL a)
  171.     {
  172.         flag=1;     valu=a;
  173.         add1=0;     add2=0;     step=0;
  174.         sum=valu*len();
  175.     }
  176. };
  178. struct Segtree
  179. {
  180.     node tree[N*4];
  181.     void down(int ind)
  182.     {
  183.         if(tree[ind].flag)
  184.         {
  185.         //两种标记都有的时候，先进行C操作的传递过程
  186.         //原因是假如先进行AB操作的话，那么c操作会将所有
  187.         //数字强制转换为value，那么AB操作被覆盖了
  188.             tree[ind*2].changeC(tree[ind].valu);
  189.             tree[ind*2+1].changeC(tree[ind].valu);
  190.             tree[ind].flag=0;
  191.         }
  192.         if(tree[ind].add1||tree[ind].add2||tree[ind].step)
  193.         {
  194.             //只要有一个不是0就说明了有AB操作的延时标记
  195.             LL add1=tree[ind].add1,add2=tree[ind].add2;
  196.             LL k=tree[ind].step;
  197.             LL mid=add1+k*(tree[ind*2].len()-1);
  199.             tree[ind*2].changeAB(add1,mid,k);
  200.             tree[ind*2+1].changeAB(mid+k,add2,k);
  201.             tree[ind].add1=0;    tree[ind].add2=0;
  202.             tree[ind].step=0;
  203.         }
  204.     }
  205.     void build(LL left,LL right,LL ind)
  206.     {
  207.         tree[ind].left=left;    tree[ind].right=right;
  208.         tree[ind].add1=0;        tree[ind].add2=0;
  209.         tree[ind].sum=0;        tree[ind].valu=0;
  210.         tree[ind].step=0;
  211.         if(left!=right)
  212.         {
  213.             LL mid=tree[ind].mid();
  214.             build(left,mid,ind*2);
  215.             build(mid+1,right,ind*2+1);
  216.         }
  217.     }
  218.     void updataAB(LL be,LL end,LL ind,LL step)
  219.     {
  220.         LL left=tree[ind].left,right=tree[ind].right;
  221.         if(be<=left&&right<=end)
  222.         {
  223.             LL st,ed;
  224.             if(step>=0) {st=left-be+1;ed=right-be+1;}
  225.             else {st=end-left+1;ed=end-right+1;}
  226.             //子区间也是只记录端点的值
  227.             tree[ind].changeAB(st,ed,step);
  228.         }
  229.         else
  230.         {
  231.             down(ind);
  232.             LL mid=tree[ind].mid();
  233.             if(be<=mid) updataAB(be,end,ind*2,step);
  234.             if(end>mid) updataAB(be,end,ind*2+1,step);
  235.             tree[ind].sum=tree[ind*2].sum+tree[ind*2+1].sum;
  236.         }
  237.     }
  238.     void updataC(LL be,LL end,LL ind,LL valu)
  239.     {
  240.         LL left=tree[ind].left,right=tree[ind].right;
  241.         if(be<=left&&right<=end) tree[ind].changeC(valu);
  242.         else
  243.         {
  244.             down(ind);
  245.             LL mid=tree[ind].mid();
  246.             if(be<=mid) updataC(be,end,ind*2,valu);
  247.             if(end>mid) updataC(be,end,ind*2+1,valu);
  248.             tree[ind].sum=tree[ind*2].sum+tree[ind*2+1].sum;
  249.         }
  250.     }
  251.     LL query(LL be,LL end,LL ind)
  252.     {
  253.         LL left=tree[ind].left,right=tree[ind].right;
  254.         if(be<=left&&right<=end) return tree[ind].sum;
  255.         else
  256.         {
  257.             down(ind);
  258.             LL mid=tree[ind].mid();
  259.             LL sum1=0,sum2=0;
  260.             if(be<=mid) sum1=query(be,end,ind*2);
  261.             if(end>mid) sum2=query(be,end,ind*2+1);
  262.             return sum1+sum2;
  263.         }
  264.     }
  265. }seg;
  267. int main()
  268. {
  270.     int n;
  271.     while(scanf("%d",&n)!=EOF)
  272.     {
  273.         seg.build(1,N-5,1); //建立一棵树
  274.         for(int i=0;i<n;i++)
  275.         {
  276.             char str[10];
  277.             LL a,b,c;
  278.             scanf("%s",str);
  279.             if(str[0]=='A')
  280.             {
  281.                 scanf("%lld%lld",&a,&b);
  282.                 seg.updataAB(a,b,1,1);
  283.             }
  284.             else if(str[0]=='B')
  285.             {
  286.                 scanf("%lld%lld",&a,&b);
  287.                 seg.updataAB(a,b,1,-1);
  288.             }
  289.             else if(str[0]=='C')
  290.             {
  291.                 scanf("%lld%lld%lld",&a,&b,&c);
  292.                 seg.updataC(a,b,1,c);
  293.             }
  294.             else
  295.             {
  296.                 scanf("%lld%lld",&a,&b);
  297.                 printf("%lld\n",seg.query(a,b,1));
  298.             }
  299.         }
  300.     }
  301.     return 0;
  302. }

发表评论

表情：
评论列表 （有 0 条评论，357人围观）

还没有评论，来说两句吧...

相关阅读

    相关 线段树区间更新

    线段树成段更新延迟标记理解 区间更新是指每次更新的时候更新的是一个区间里面的所有值，例如将区间\[l,r\]内的所有点都加或者减去一个数，或者替换成一个数字等等.因为区间更新

    淩亂°似流年淩亂°似流年/ 0 赞/ 358 阅读