Billboard（线段树区间更新与求值）

╰+攻爆jí腚メ 2022-08-01 11:12 201阅读 0赞

# Billboard #

**Time Limit: 20000/8000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)  
Total Submission(s): 13621    Accepted Submission(s): 5853**

Problem Description

At the entrance to the university, there is a huge rectangular billboard of size h\*w (h is its height and w is its width). The board is the place where all possible announcements are posted: nearest programming competitions, changes in the dining room menu, and other important information.  
  
On September 1, the billboard was empty. One by one, the announcements started being put on the billboard.  
  
Each announcement is a stripe of paper of unit height. More specifically, the i-th announcement is a rectangle of size 1 \* wi.  
  
When someone puts a new announcement on the billboard, she would always choose the topmost possible position for the announcement. Among all possible topmost positions she would always choose the leftmost one.  
  
If there is no valid location for a new announcement, it is not put on the billboard (that's why some programming contests have no participants from this university).  
  
Given the sizes of the billboard and the announcements, your task is to find the numbers of rows in which the announcements are placed.

Input

There are multiple cases (no more than 40 cases).  
  
The first line of the input file contains three integer numbers, h, w, and n (1 <= h,w <= 10^9; 1 <= n <= 200,000) - the dimensions of the billboard and the number of announcements.  
  
Each of the next n lines contains an integer number wi (1 <= wi <= 10^9) - the width of i-th announcement.

Output

For each announcement (in the order they are given in the input file) output one number - the number of the row in which this announcement is placed. Rows are numbered from 1 to h, starting with the top row. If an announcement can't be put on the billboard, output "-1" for this announcement.

Sample Input

3 5 5
    2
    4
    3
    3
    3

Sample Output

1
    2
    1
    3
    -1

Author

hhanger@zju

Source

[HDOJ 2009 Summer Exercise（5）][HDOJ 2009 Summer Exercise_5]

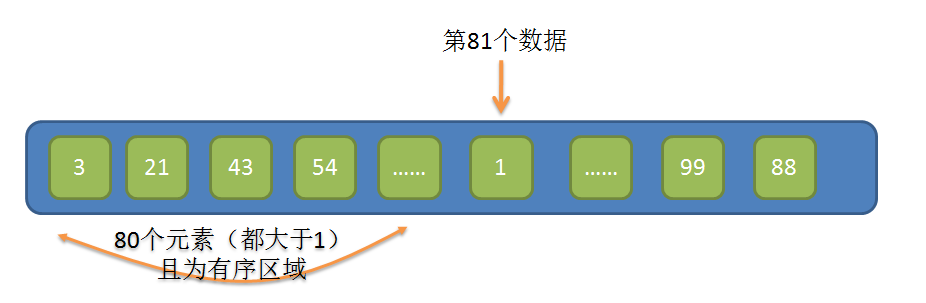
**这一题是线段树。为什么这么说呢？**

1.  题目大意: 
2.  有一块h\*w的矩形广告板，要往上面贴广告; 
3.  然后给n个1\*wi的广告，要求把广告贴上去; 
4.  而且要求广告要尽量往上贴并且尽量靠左; 
5.  求第n个广告的所在的位置，不能贴则为-1;

我们想一下线段树的存储原理：

1.序号从低往高存，直到找到像(1,1)(2,2)...(n,n)这样的才算停止！

2.每一次都是从低往高计算

这不正是这一题的需求吗？

我们先画出example里的图

![Image 1][]

从左到右依次(1,1)(2,2)(3,3)....(5,5)

所以这一题是线段树

每次检查就可以了

注意一下当n小于h的时候应该以n为标准！

#include<cstdio>
    #include<iostream>
    #include<cstring>
    #include<string>
    #include<algorithm>
    using namespace std;
    const int maxn = 200010;
    int MAX[maxn*4];
    int h,w,n;
    void PushUp(int rt)
    {
        MAX[rt] = max(MAX[rt*2], MAX[rt*2+1]);
    }
    void build(int l,int r,int rt)
    {
        MAX[rt]=w;
        if(l==r)
        {
            return;
        }
        int m=(l+r)/2;
        build(l,m,rt*2);
        build(m+1,r,rt*2+1);
    }
    int query(int x,int l,int r,int rt)
    {
        int sum;
        if (l == r)
        {
            MAX[rt]-=x;
            return l;
        }
        int m=(l+r)/2;
        if(MAX[rt*2]>=x)
        {
            sum=query(x,l,m,rt*2);
        }
        else
        {
            sum=query(x,m+1,r,rt*2+1);
        }
        PushUp(rt);  //更新父节点的值
        return sum;
    }
    int main()
    {
        int x;
        while (scanf("%d%d%d", &h, &w, &n) != EOF)
        {
            if(h>n)
            {
                h=n;
            }
            build(1,h,1);//先建树
            while(n--)
            {
                scanf("%d",&x);
                if(MAX[1]<x)
                {
                     printf("-1\n");
                }
                else
                {
                    printf("%d\n", query(x, 1, h, 1));
                }
            }
        }
    }

[HDOJ 2009 Summer Exercise_5]: http://acm.hdu.edu.cn/search.php?field=problem&key=HDOJ+2009+Summer+Exercise%A3%A85%A3%A9&source=1&searchmode=source
[Image 1]: