目标跟踪之Horn-Schunck光流法

缺乏、安全感 2022-08-09 14:59 226阅读 0赞

关于光流法请看我之前的博客Lukas-Kanade光流法。这里介绍Horn-Schunck光流法。

Horn-Schunck光流法求得的是稠密光流，需要对每一个像素计算光流值，计算量比较大。而Lucas-Kanade光流法只需计算若干点的光流，是一种稀疏光流。

数学原理这里就不介绍了，直接说算法步骤。

用uij与vij分别表示图像像素点(i，j)处的水平方向光流值与垂直方向光流值，每次迭代后的更新方程为

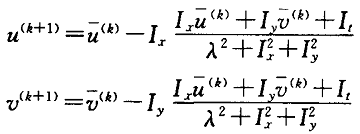
20151030145919176

n为迭代次数，lamda反映了对图像数据及平滑约束的可信度，当图像数据本身含有较大噪声时，此时需要加大lamda的值，相反，当输入图像含有较少的噪声时，此时可减小lamda的值。

代表u邻域与v邻域的平均值，一般采用相应4邻域内的均值

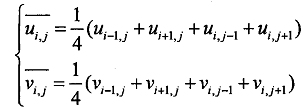
20151029233433165

也可以采用3*3、5*5的窗口用模板平滑，窗口不宜过大，过大会破坏光流假设。

Ix、Iy分别是图像对x、y的偏导数。It是两帧图像间对时间的导数。

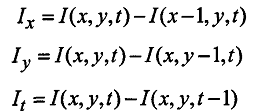
20151030104632199

当然你也可以考虑相邻像素及相邻两帧图像的影响，Horn-Schunck 提出通过 4 次有限差分来得到

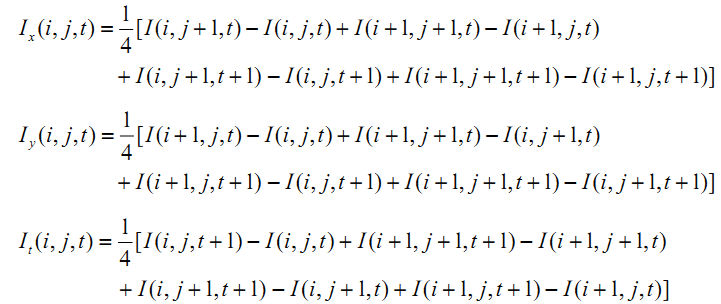
20151030113610321

这里只考虑了前后两帧图像。考虑连续三帧图像的话有如下方法：

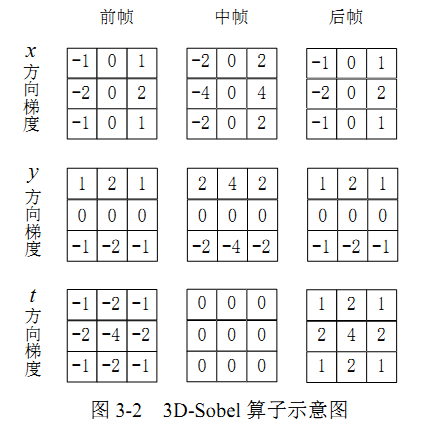
一种性能更优的 3D-Sobel 算子 如下图所示。该算子在x 、y 、t方向上分别使用不同的模板对连续3帧图像进行卷积计算 得出中间帧的位于模板中心的像素在三个方向上的梯度 。

20151030114019786

迭代一定次数后u、v收敛，光流计算停止。在实际的计算中迭代初值可取U(0) =0、V(0)=0。

算法改进

对于一般场景基本等式只有在图像中灰度梯度值较大的点处才成立。因此为了增强算法的稳定性和准确性 我们仅在梯度较大的点处才使用亮度恒常性约束，而在梯度较小的点处只使用流场一致性约束。定义如下权函数

20151030114707342

下面是我的实现，使用了图像金字塔，关于图像金字塔，请看Lukas-Kanade光流法。（写代码时传错一个参数，调了几个小时哭）

  1. #ifndef __HORNSCHUNCK__
  2. #define __HORNSCHUNCK__
  3. class HornSchunckTracker
  4. {
  5. private:
  6.     unsigned int max_pyramid_layer;
  7.     unsigned int original_imgH;
  8.     unsigned int original_imgW;
  9.     BYTE**pre_pyr;//the pyramid of previous frame image,img1_pyr[0] is of max size
  10.     BYTE**next_pyr;//the frame after img1_pyr
  11.     int*height;
  12.     int*width;
  13.     double*optical_field_U;
  14.     double*optical_field_V;
  15.     bool isusepyramid;
  16.     double lamda;//取20
  17.     const double precision = 1;
  18.     const int maxiteration=300;
  19.     double threshold;//最小的光流阈值
  20.     double scale_factor;//缩放因子
  21. private:
  22.     void get_max_pyramid_layer();
  23.     void pyramid_down(BYTE*&src_gray_data, const int src_h,
  24.         const int src_w, BYTE*& dst, int&dst_h, int&dst_w);
  25.     void pyramid_up(double*src,int srcW,int srcH,double*dst,int dstW,int dstH);
  26.     void lowpass_filter(double*&src, const int H, const int W, double*&smoothed);
  27.     void get_fx_fy_ft(BYTE*img1, BYTE*img2, int w, int h, double*fx, double*fy, double*ft);
  28.     void build_pyramid(BYTE**&original_gray);
  29.     double get_average4(double*src, const int height, const int width, const int i, const int j);
  30.     void  bilinear(double* lpSrc, double* lpDst, int nW, int nH, int H1, int W1);
  31.     void  bilinear(BYTE* lpSrc, BYTE* lpDst, int nW, int nH, int H1, int W1);
  35. public:
  36.     HornSchunckTracker();
  37.     ~HornSchunckTracker();
  38.     void get_pre_frame(BYTE*&gray);//use only at the beginning
  39.     void discard_pre_frame();
  40.     //set the next frame as pre_frame,must dicard pre_pyr in advance
  41.     void get_pre_frame();
  42.     //use every time,must after using get_pre_frame(BYTE**pyr)
  43.     void get_next_frame(BYTE*&gray);
  44.     void get_info(const int nh, const int nw);
  45.     void set_paras(double lamda,double threshold,double scalefactor);
  46.     void run_single_frame();
  47.     void HornSchunck();
  48.     void get_optical_flow(double*&u, double*&v);
  49. };
  51. #endif
  57. #include "stdafx.h"
  58. #include "HornSchunckTracker.h"
  61. HornSchunckTracker::HornSchunckTracker()
  62. {
  63.     isusepyramid = true;
  64. }
  67. HornSchunckTracker::~HornSchunckTracker()
  68. {
  69.     for (int i = 0; i < max_pyramid_layer; i++)
  70.     {
  71.         if (pre_pyr[i])
  72.             delete[]pre_pyr[i];
  73.         if (next_pyr[i])
  74.             delete[]next_pyr[i];
  75.     }
  76.     delete[]pre_pyr;
  77.     delete[]next_pyr;
  78.     if (height)
  79.         delete[]height;
  80.     if (width)
  81.         delete[]width;
  83. }
  84. void HornSchunckTracker::get_max_pyramid_layer()
  85. {
  86.     double minsize = 80;
  87.     double temp = original_imgH > original_imgW ?
  88.     original_imgW : original_imgH;
  89.     double tt = log(temp / minsize) / log(scale_factor);
  90.     if (tt>4)
  91.     {
  92.         max_pyramid_layer = 5;
  93.         return;
  94.     }
  96.     max_pyramid_layer = tt;
  97. }
  99. void HornSchunckTracker::build_pyramid(BYTE**&pyramid)
  100. {
  101.     for (int i = 1; i < max_pyramid_layer; i++)
  102.     {
  103.         pyramid_down(pyramid[i - 1], height[i - 1],
  104.             width[i - 1], pyramid[i], height[i], width[i]);
  105.     }
  106. }
  109. void HornSchunckTracker::pyramid_down(BYTE*&src_gray_data,
  110.     const int src_h, const int src_w, BYTE*& dst, int&dst_h, int&dst_w)
  111. {
  112.     dst_h = src_h / scale_factor;
  113.     dst_w = src_w / scale_factor;
  115.     assert(dst_w > 3 && dst_h > 3);
  116.     //BYTE*smoothed = new BYTE[src_h*src_w];
  117.     dst = new BYTE[dst_h*dst_w];
  118.     //lowpass_filter(src_gray_data, src_h, src_w,smoothed);
  119.     bilinear(src_gray_data, dst, src_w, src_h, dst_h, dst_w);
  121.     /*for (int i = 0; i < dst_h - 1; i++)
  122.         for (int j = 0; j < dst_w - 1; j++)
  123.         {
  124.             int srcY = 2 * i + 1;
  125.             int srcX = 2 * j + 1;
  126.             double re = src_gray_data[srcY*src_w + srcX] * 0.25;
  127.             re += src_gray_data[(srcY - 1)*src_w + srcX] * 0.125;
  128.             re += src_gray_data[(srcY + 1)*src_w + srcX] * 0.125;
  129.             re += src_gray_data[srcY*src_w + srcX - 1] * 0.125;
  130.             re += src_gray_data[srcY*src_w + srcX + 1] * 0.125;
  131.             re += src_gray_data[(srcY - 1)*src_w + srcX + 1] * 0.0625;
  132.             re += src_gray_data[(srcY - 1)*src_w + srcX - 1] * 0.0625;
  133.             re += src_gray_data[(srcY + 1)*src_w + srcX - 1] * 0.0625;
  134.             re += src_gray_data[(srcY + 1)*src_w + srcX + 1] * 0.0625;
  135.             dst[i*dst_w + j] = re;
  136.         }
  137.     for (int i = 0; i < dst_h; i++)
  138.         dst[i*dst_w + dst_w - 1] = dst[i*dst_w + dst_w - 2];
  139.     for (int i = 0; i < dst_w; i++)
  140.         dst[(dst_h - 1)*dst_w + i] = dst[(dst_h - 2)*dst_w + i];*/
  141. }
  144. void HornSchunckTracker::get_pre_frame(BYTE*&gray)//use only at the beginning
  145. {
  146.     pre_pyr[0] = gray;
  147.     build_pyramid(pre_pyr);
  148.     //save_gray("1.bmp", pre_pyr[1], height[1], width[1]);
  149. }
  151. void  HornSchunckTracker::discard_pre_frame()
  152. {
  153.     for (int i = 0; i < max_pyramid_layer; i++)
  154.         delete[]pre_pyr[i];
  155. }
  156. //set the next frame as pre_frame,must dicard pre_pyr in advance
  157. void  HornSchunckTracker::get_pre_frame()
  158. {
  159.     for (int i = 0; i < max_pyramid_layer; i++)
  160.         pre_pyr[i] = next_pyr[i];
  161. }
  162. //use every time,must after using get_pre_frame(BYTE**pyr)
  163. void  HornSchunckTracker::get_next_frame(BYTE*&gray)
  164. {
  165.     next_pyr[0] = gray;
  166.     build_pyramid(next_pyr);
  167.     //save_gray("1.bmp", next_pyr[1], height[1], width[1]);
  168. }
  170. void HornSchunckTracker::get_info(const int nh, const int nw)
  171. {
  172.     original_imgH = nh;
  173.     original_imgW = nw;
  174.     if (isusepyramid)
  175.         get_max_pyramid_layer();
  176.     else
  177.         max_pyramid_layer = 1;
  178.     pre_pyr = new BYTE*[max_pyramid_layer];
  179.     next_pyr = new BYTE*[max_pyramid_layer];
  180.     height = new int[max_pyramid_layer];
  181.     width = new int[max_pyramid_layer];
  182.     height[0] = nh;
  183.     width[0] = nw;
  184. }
  187. //低通滤波
  188. void HornSchunckTracker::lowpass_filter(double*&src, const int H, const int W, double*&smoothed)
  189. {
  190.     //tackle with border
  191.     for (int i = 0; i < H; i++)
  192.     {
  193.         smoothed[i*W] = src[i*W];
  194.         smoothed[i*W + W - 1] = src[i*W + W - 1];
  195.     }
  196.     for (int i = 0; i < W; i++)
  197.     {
  198.         smoothed[i] = src[i];
  199.         smoothed[(H - 1)*W + i] = src[(H - 1)*W + i];
  200.     }
  202.     for (int i = 1; i < H - 1; i++)
  203.         for (int j = 1; j < W - 1; j++)
  204.         {
  205.             double re = 0;
  206.             re += src[i*W + j] * 0.25;
  207.             re += src[(i - 1)*W + j] * 0.125;
  208.             re += src[i*W + j + 1] * 0.125;
  209.             re += src[i*W + j - 1] * 0.125;
  210.             re += src[(i + 1)*W + j] * 0.125;
  211.             re += src[(i - 1)*W + j - 1] * 0.0625;
  212.             re += src[(i + 1)*W + j - 1] * 0.0625;
  213.             re += src[(i - 1)*W + j + 1] * 0.0625;
  214.             re += src[(i + 1)*W + j + 1] * 0.0625;
  215.             smoothed[i*W + j] = re;
  216.         }
  218. }
  220. void HornSchunckTracker::get_fx_fy_ft(BYTE*img1, BYTE*img2, int w, int h, double*fx, double*fy, double*ft)
  221. {
  222.     for (int i = 0; i < h - 1; i++)
  223.         for (int j = 0; j < w - 1; j++)
  224.         {
  225.             fx[i*w + j] = 0.25*(img1[i*w + j + 1] - img1[i*w + j] + img1[(i + 1)*w + j + 1] - img1[(i + 1)*w + j]
  226.                 + img2[i*w + j + 1] - img2[i*w + j] + img2[(i + 1)*w + j + 1] - img2[(i + 1)*w + j]);
  227.             fy[i*w + j] = 0.25 * (img1[(i + 1)*w + j] - img1[i*w + j] +img1[(i + 1)*w + j + 1] - img1[i*w + j + 1]
  228.                 + img2[(i + 1)*w + j] - img2[i*w + j] + img2[(i + 1)*w + j + 1] - img2[i*w + j + 1]);
  229.             ft[i*w + j] = 0.25 * (img2[i*w + j] - img1[i*w + j] +img2[(i + 1)*w + j] - img1[(i + 1)*w + j] +
  230.                 img2[(i + 1)*w + j + 1] - img1[(i + 1)*w + j + 1] + img2[i*w + j + 1] - img1[i*w + j + 1]);
  231.         }
  232.     for (int i = 0; i < h; i++)
  233.     {
  234.         //fx[i*w] = fx[i*w + w - 2];
  235.         fx[i*w + w - 1] = fx[i*w + w - 2];
  236.         //fy[i*w] = fy[i*w + w - 2];
  237.         fy[i*w + w - 1] = fy[i*w + w - 2];
  238.         //ft[i*w] = ft[i*w + w - 2];
  239.         ft[i*w + w - 1] = ft[i*w + w - 2];
  240.     }
  241.     for (int j = 0; j < w; j++)
  242.     {
  243.         //fx[j] = fx[h + j];
  244.         fx[(h - 1)*w + j] = fx[(h - 2)*w + j];
  245.         //fy[j] = fy[h + j];
  246.         fy[(h - 1)*w + j] = fy[(h - 2)*w + j];
  247.         //ft[j] = ft[h + j];
  248.         ft[(h - 1)*w + j] = ft[(h - 2)*w + j];
  249.     }
  251. }
  252. //取得计算得到的光流值，u、v为out型参数
  253. void HornSchunckTracker::get_optical_flow(double*&u, double*&v)
  254. {
  255.     assert(optical_field_U&&optical_field_V);
  256.     u = optical_field_U;
  257.     v = optical_field_V;
  258. }
  260. //int save_gray(char * savebmp_file, LPBYTE gray, int height, int width);
  261. //返回求得的光流场，大小为原始图像大小
  262. void HornSchunckTracker::HornSchunck()
  263. {
  264.     //save_gray("22.bmp", pre_pyr[0], height[0], width[0]);
  265.     //初始化光流场为0
  266.     if (optical_field_U)
  267.         delete[]optical_field_U;
  268.     if (optical_field_V)
  269.         delete[]optical_field_V;
  270.     optical_field_U = new double[width[max_pyramid_layer - 1]
  271.         * height[max_pyramid_layer - 1]];
  272.     optical_field_V = new double[width[max_pyramid_layer - 1]
  273.         * height[max_pyramid_layer - 1]];
  274.     memset(optical_field_U, 0, sizeof(double)*width[max_pyramid_layer - 1]
  275.         * height[max_pyramid_layer - 1]);
  276.     memset(optical_field_V, 0, sizeof(double)*width[max_pyramid_layer - 1]
  277.         * height[max_pyramid_layer - 1]);
  279.     //使用金字塔计算光流
  280.     for (int i = max_pyramid_layer - 1; i >= 0; i--)
  281.     {
  282.         double*Ix = new double[width[i] * height[i]];
  283.         double*Iy = new double[width[i] * height[i]];
  284.         double*It = new double[width[i] * height[i]];
  285.         //求偏导
  286.         get_fx_fy_ft(pre_pyr[i], next_pyr[i], width[i], height[i], Ix, Iy, It);
  288.         //将光流场平滑
  289.         double*smoothed_U = new double[width[i] * height[i]];
  290.         double*smoothed_V = new double[width[i] * height[i]];
  292.         if (i == max_pyramid_layer - 1)
  293.         {
  294.             memset(smoothed_U, 0, sizeof(double)*width[i] * height[i]);
  295.             memset(smoothed_V, 0, sizeof(double)*width[i] * height[i]);
  296.         }
  297.         else
  298.         {
  299.             lowpass_filter(optical_field_U, height[i], width[i], smoothed_U);
  300.             lowpass_filter(optical_field_V, height[i], width[i], smoothed_V);
  301.         }
  302.         double error = 1000000;
  303.         int iteration = 0;
  304.         //迭代计算每个像素的光流，直到收敛或达到最大迭代次数
  305.         while (error > precision&&iteration < maxiteration)
  306.         {
  307.             iteration++;
  308.             error = 0;
  309.             //计算该层金字塔的光流
  310.             for (int j = 0; j < height[i]; j++)
  311.                 for (int k = 0; k < width[i]; k++)
  312.                 {
  314.                     //采用改进方法，光流速度需大于阈值，这样不仅准确度增加，计算量也会减小
  315.                     double w = Ix[j*width[i] + k] * Ix[j*width[i] + k]
  316.                         + Iy[j*width[i] + k] * Iy[j*width[i] + k] > threshold ? 1 : 0;
  318.                     double u_pre = optical_field_U[j*width[i] + k];
  319.                     double v_pre = optical_field_V[j*width[i] + k];
  321.                     double utemp = smoothed_U[j*width[i] + k];//get_average4(optical_field_U, height[i], width[i], j, k);
  322.                     double vtemp = smoothed_V[j*width[i] + k]; //get_average4(optical_field_V, height[i], width[i], j, k);
  323.                     double denominator = lamda + w*(Ix[j*width[i] + k] * Ix[j*width[i] + k]
  324.                         + Iy[j*width[i] + k] * Iy[j*width[i] + k]);
  325.                     double numerator = Ix[j*width[i] + k] * utemp + Iy[j*width[i] + k] *
  326.                         vtemp + It[j*width[i] + k];
  328.                     optical_field_U[j*width[i] + k] = utemp - Ix[j*width[i] + k] *w*numerator / denominator;
  330.                     optical_field_V[j*width[i] + k] = vtemp - Iy[j*width[i] + k] *w*numerator / denominator;
  332.                     error += pow(optical_field_U[j*width[i] + k] - u_pre,2) +
  333.                         pow(optical_field_V[j*width[i] + k] - v_pre,2);
  334.                 }
  336.             //下一次迭代前重新平滑光流场
  337.             if (error >exp(double(max_pyramid_layer-i))*precision&&iteration < maxiteration)
  338.             {
  339.                 lowpass_filter(optical_field_U, height[i], width[i], smoothed_U);
  340.                 lowpass_filter(optical_field_V, height[i], width[i], smoothed_V);
  341.             }
  342.         }
  343.         delete[]smoothed_U, smoothed_V,Ix,Iy,It;
  345.         if (i == 0)//得到最终光流场
  346.         {
  347.             return;
  348.         }
  350.         //下一层的光流场
  351.         double*new_of_u = new double[width[i - 1] * height[i - 1]];
  352.         double*new_of_v = new double[width[i - 1] * height[i - 1]];
  355.         //上采样
  356.         pyramid_up(optical_field_U, width[i], height[i], new_of_u, width[i - 1], height[i - 1]);
  357.         pyramid_up(optical_field_V, width[i], height[i], new_of_v, width[i - 1], height[i - 1]);
  358.         //将每个像素的光流按缩放因子放大，得到下一层的光流场的初值
  359.         //double scale = double(height[i - 1]) / height[i];
  360.         for (int j = 0; j < height[i - 1]; j++)
  361.             for (int k = 0; k < width[i - 1]; k++)
  362.             {
  363.                 new_of_u[j*width[i - 1] + k] *= scale_factor;
  364.                 new_of_v[j*width[i - 1] + k] *= scale_factor;
  365.             }
  366.         delete[]optical_field_U, optical_field_V;
  367.         optical_field_U = new_of_u;
  368.         optical_field_V = new_of_v;
  369.     }
  370. }
  372. //上采样，采用双线性插值，用双立方插值应该更精确
  373. void HornSchunckTracker::pyramid_up(double*src, int srcW, int srcH, double*dst, int dstW, int dstH)
  374. {
  375.     bilinear(src, dst, srcW, srcH, dstH, dstW);
  376. }
  378. //双线性插值
  379. void  HornSchunckTracker::bilinear(double* lpSrc, double* lpDst, int nW, int nH, int H1, int W1)
  380. {
  381.     float fw = float(nW) / W1;
  382.     float fh = float(nH) / H1;
  383.     int y1, y2, x1, x2, x0, y0;
  384.     float fx1, fx2, fy1, fy2;
  386.     for (int i = 0; i < H1; i++)
  387.     {
  388.         y0 = i*fh;
  389.         y1 = int(y0);
  390.         if (y1 == nH - 1)    y2 = y1;
  391.         else y2 = y1 + 1;
  393.         fy1 = y1 - y0;
  394.         fy2 = 1.0f - fy1;
  395.         for (int j = 0; j < W1; j++)
  396.         {
  397.             x0 = j*fw;
  398.             x1 = int(x0);
  399.             if (x1 == nW - 1)    x2 = x1;
  400.             else x2 = x1 + 1;
  402.             fx1 = y1 - y0;
  403.             fx2 = 1.0f - fx1;
  405.             float s1 = fx1*fy1;
  406.             float s2 = fx2*fy1;
  407.             float s3 = fx2*fy2;
  408.             float s4 = fx1*fy2;
  410.             double c1, c2, c3, c4;
  411.             c1 = lpSrc[y1*nW + x1];
  412.             c2 = lpSrc[y1*nW + x2];
  413.             c3 = lpSrc[y2*nW + x1];
  414.             c4 = lpSrc[y2*nW + x2];
  416.             double r;
  417.             r = (c1*s3) + (c2*s4) + (c3*s2) + (c4*s1);
  418.             lpDst[i*W1 + j] = r;
  419.         }
  420.     }
  421. }
  422. //双线性插值
  423. void  HornSchunckTracker::bilinear(BYTE* lpSrc, BYTE* lpDst, int nW, int nH, int H1, int W1)
  424. {
  425.     float fw = float(nW) / W1;
  426.     float fh = float(nH) / H1;
  427.     int y1, y2, x1, x2, x0, y0;
  428.     float fx1, fx2, fy1, fy2;
  430.     for (int i = 0; i < H1; i++)
  431.     {
  432.         y0 = i*fh;
  433.         y1 = int(y0);
  434.         if (y1 == nH - 1)    y2 = y1;
  435.         else y2 = y1 + 1;
  437.         fy1 = y1 - y0;
  438.         fy2 = 1.0f - fy1;
  439.         for (int j = 0; j < W1; j++)
  440.         {
  441.             x0 = j*fw;
  442.             x1 = int(x0);
  443.             if (x1 == nW - 1)    x2 = x1;
  444.             else x2 = x1 + 1;
  446.             fx1 = y1 - y0;
  447.             fx2 = 1.0f - fx1;
  449.             float s1 = fx1*fy1;
  450.             float s2 = fx2*fy1;
  451.             float s3 = fx2*fy2;
  452.             float s4 = fx1*fy2;
  454.             double c1, c2, c3, c4;
  455.             c1 = lpSrc[y1*nW + x1];
  456.             c2 = lpSrc[y1*nW + x2];
  457.             c3 = lpSrc[y2*nW + x1];
  458.             c4 = lpSrc[y2*nW + x2];
  460.             double r;
  461.             r = (c1*s3) + (c2*s4) + (c3*s2) + (c4*s1);
  462.             lpDst[i*W1 + j] = BYTE(r);
  463.         }
  464.     }
  465. }
  467. void HornSchunckTracker::set_paras(double lamda, double threshold, double scalefactor)
  468. {
  469.     this->lamda = lamda;
  470.     this->threshold = threshold;
  471.     scale_factor = scalefactor;
  472. }
  476. //double HornSchunckTracker::get_average4(double*src, const int height, const int width, const int i, const int j)
  477. //{
  478. //    if (j < 0 || j >= width) return 0;
  479. //    if (i < 0 || i >= height) return 0;
  480. //
  481. //    double val = 0.0;
  482. //    int tmp = 0;
  483. //    if ((i - 1) >= 0){
  484. //        ++tmp;
  485. //        val += src[(i - 1)*width + j];
  486. //    }
  487. //    if (i + 1<height){
  488. //        ++tmp;
  489. //        val += src[(i + 1)*width + j];
  490. //    }
  491. //    if (j - 1 >= 0){
  492. //        ++tmp;
  493. //        val += src[i*width + j - 1];
  494. //    }
  495. //    if (j + 1<width){
  496. //        ++tmp;
  497. //        val += src[i*width + j + 1];
  498. //    }
  499. //    return val / tmp;
  500. //
  501. //}

下面是两帧图像和检测结果

20151030224744051 20151030224757826

20151030224949095

可以看出对边缘的光流检测较好，内部点的光流检测较难。

发表评论

表情：
评论列表 （有 0 条评论，226人围观）

还没有评论，来说两句吧...

相关阅读

    相关 光流法基本原理

    摘自百度百科 光流是一种简单实用的图像运动的表达方式\[1\]，通常定义为一个图像序列中的图像亮度模式的表观运动，即空间物体表面上的点的运动速度在视觉传感器的成像平面上的表达

    深藏阁楼爱情的钟深藏阁楼爱情的钟/ 0 赞/ 253 阅读

    相关 Lucas-Kanade光流法

    Lucas-Kanade光流法是通过先在前后两帧图像里分别建立一个固定大小窗口，然后找到让两个窗口间像素强度差的平方和最小的位移。然后将窗口内像素的移动近似为这样的位移向量，然

    蔚落蔚落/ 0 赞/ 353 阅读