430-动态规划算法-LCS最长公共子序列-蒲公英云

430-动态规划算法-LCS最长公共子序列

灰太狼 2022-09-05 05:15 292阅读 0赞

LCS最长公共子序列

LCS：求两个序列的最长公共子序列的长度
子串（字符必须是连续的）
但是子序列不一定是连续的
例如：
helloworld
hlweord
这2个子序列的最长公共子序列是： hlweord

我们要求
X : X1,X2…Xn
Y: Y1,Y2…Ym
求两个序列的LCS最长公共子序列长度
我们进行子问题的划分

我们先用分治算法来解决

在这里插入图片描述

我们看看算法的思维图解：

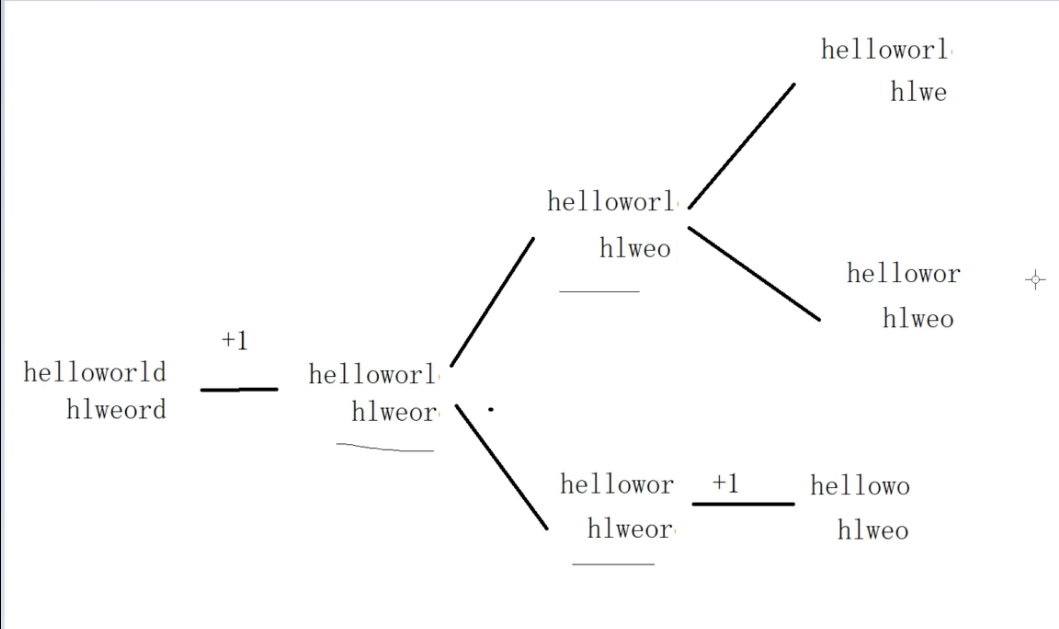
在这里插入图片描述
继续划分，我们发现会出现子问题的重复求解！

子问题重叠了，被重复求解，所以，我们应该使用动态规划算法去解决，动态规划算法对子问题的求解是有记忆性的！

递归版本的动态规划求解

在这里插入图片描述
我们是从后往前推的哦

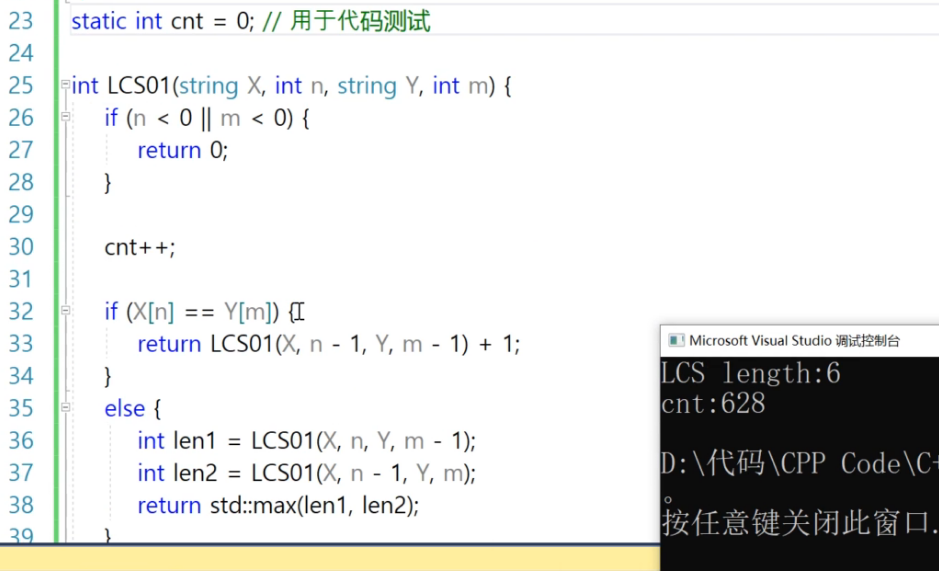
static int cnt = 0;//用于代码测试
string str1 = "helloworld";
string str2 = "hlweord";
int **dp = nullptr;//记录最长子序列的长度
int **path = nullptr;//记录最长子序列的路径
//递归实现
int LCSA(string X, int n, string Y, int m) 
{
    if (n < 0 || m < 0)//递归结束的条件
    {
        return 0;//没有公共子序列，长度是0
    }
    if (dp[n][m] >= 0) 
    {
       //查表，查子问题的解是否被求过
        return dp[n][m];//直接返回问题的解，不重复求解
    }
    cnt++;//分治算法：628次    动态规划：40次
    if (X[n] == Y[m]) 
    {
        dp[n][m] = LCS01(X, n - 1, Y, m - 1) + 1;
        path[n][m] = 1;//表示n,m 跑向 n-1,m-1 1表示走对角线(左上角)
        return dp[n][m];
    }
    else 
    {
        int len1 = LCS01(X, n, Y, m - 1);
        int len2 = LCS01(X, n - 1, Y, m);
        if (len1 >= len2) 
        {
            dp[n][m] = len1;
            path[n][m] = 2;// n,m跑向n,m-1  2表示表示走左边
        }
        else 
        {
            dp[n][m] = len2;
            path[n][m] = 3;// n,m 跑向n-1,m  3表示走上方
        }
        return dp[n][m];
    }
}

在这里插入图片描述

dp数组的打印结果是：
*代表的是-1
在这里插入图片描述
这个二维数组只是记录了相应的2个子串的LCS最长公共子序列的长度

我们还要记得释放dp这个二维数组的堆内存哦！
path数组打印的结果是：
这个二维数组记录了相应的2个子串的LCS最长公共子序列的字符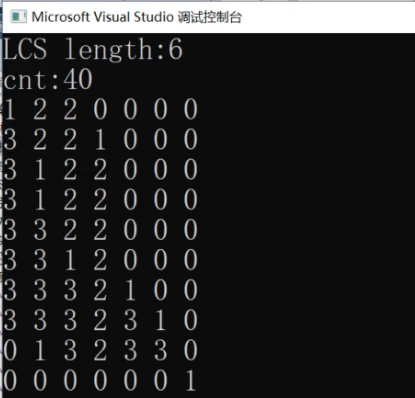在这里插入图片描述

我们根据path的定义
我们从最后一行最后一列的位置（右下角）开始走！！！
1：走对角线（左上）
2：走左边
3：走正上方

因为对角线是代表：字符相比较是相等的，所以我们看往对角线走的地方，这些地方是相应元素字符相等的地方！！！
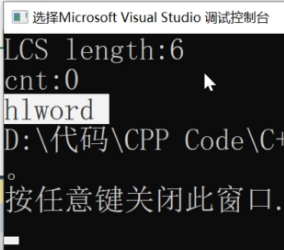
对角线的元素组成的字符串是：hlword，这个就是最长公共子序列！！！
在这里插入图片描述

非递归版本的动态规划求解

在这里插入图片描述

我们需要用二维的dp数组来求解。
因为我们需要记录3个变量，两个串和序列的长度

状态：给定的两个序列的LCS的长度
dp[n][m] : n表示第一个串的长度 m表示第二个串的长度，n行m列元素的值，记录的就是这两个串的LCS长度
非递归是从0行0列开始计算的

#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
static int cnt = 0;//用于代码测试
string str1 = "helloworld";
string str2 = "hlweord";
int **dp = nullptr;
int **path = nullptr;//记录最长子序列
//非递归实现
int LCSB(string X, int i, string Y, int j) 
{
    for (int n = 1; n <= i+1; ++n)//因为n-1不能为负数 所以从1开始 然后n<=i+1，也可以是：m==n==0的时候，直接置为1
    {
        for (int m = 1; m <= j+1; ++m)//因为m-1不能为负数 所以从1开始 然后m<=j+1
        {
            if (X[n-1] == Y[m-1]) 
            {
                dp[n][m] = 1 + dp[n - 1][m - 1];//n==0 m ==0 走对角线
                path[n][m] = 1;
            }
            else 
            {
                int len1 = dp[n-1][m];//向上面走
                int len2 = dp[n][m-1];//向左边走
                if (len1 >= len2) 
                {
                    dp[n][m] = len1;
                    path[n][m] = 3;
                } 
                else 
                {
                    dp[n][m] = len2;
                    path[n][m] = 2;
                }
            }
        }
    }
    return dp[i+1][j+1];
}
void backStrace(string str1, int n, int m)//打印最长公共子串
{
    if (n <= 0 || m <= 0)//递归结束条件
    {
        return;
    }
    if (path[n][m] == 1) 
    {
       //对应位置的元素是相等的
        backStrace(str1, n - 1, m - 1);//向对角线递归
        cout << str1[n-1];//回溯的时候再打印
    }
    else 
    {
        if (path[n][m] == 2) 
        {
            backStrace(str1, n, m - 1);//向左边递归
        }
        else 
        {
       //path[n][m] = 3
            backStrace(str1, n - 1, m);//向上方递归
        }
    }
}
int main()
{
    //dp是一个n行m列的二维数组
    int n = str1.size();
    int m = str2.size();
    dp = new int*[n+1];//n行
    for (int i = 0; i < n+1; ++i) 
    {
        dp[i] = new int[m+1];//m列
        for (int j = 0; j < m+1; ++j) 
        {
            //dp[i][j] = -1;
            dp[i][j] = 0;//初始化为0
        }
    }
    path = new int*[n+1];//n行
    for (int i = 0; i < n+1; ++i) 
    {
        path[i] = new int[m+1]();//m列
    }
    int size = LCS(str1, n-1, str2, m-1);
    cout << "LCS length:" << size << endl;
    cout << "cnt:" << cnt << endl;
    //backStrace(str1, n-1, m-1);
    backStrace(str1, n, m);
    //for (int i = 0; i < n; ++i) {   //行
    //    for (int j = 0; j < m; ++j) { //列
    //        cout << path[i][j] << " ";
    //    }
    //    cout << endl;
    //}
    //释放dp数组内存
    return 0;
}