Leetcode 329. 矩阵中的最长递增路径（DAY 169）---- LeetCode 精选 TOP 面试题-蒲公英云

Leetcode 329. 矩阵中的最长递增路径（DAY 169）---- LeetCode 精选 TOP 面试题

清疚 2022-09-11 05:13 242阅读 0赞

文章目录

- 原题题目
- 代码实现（首刷超时 TLE 135/138）
- 代码实现（首刷自解回溯法DFS+记忆化）

原题题目

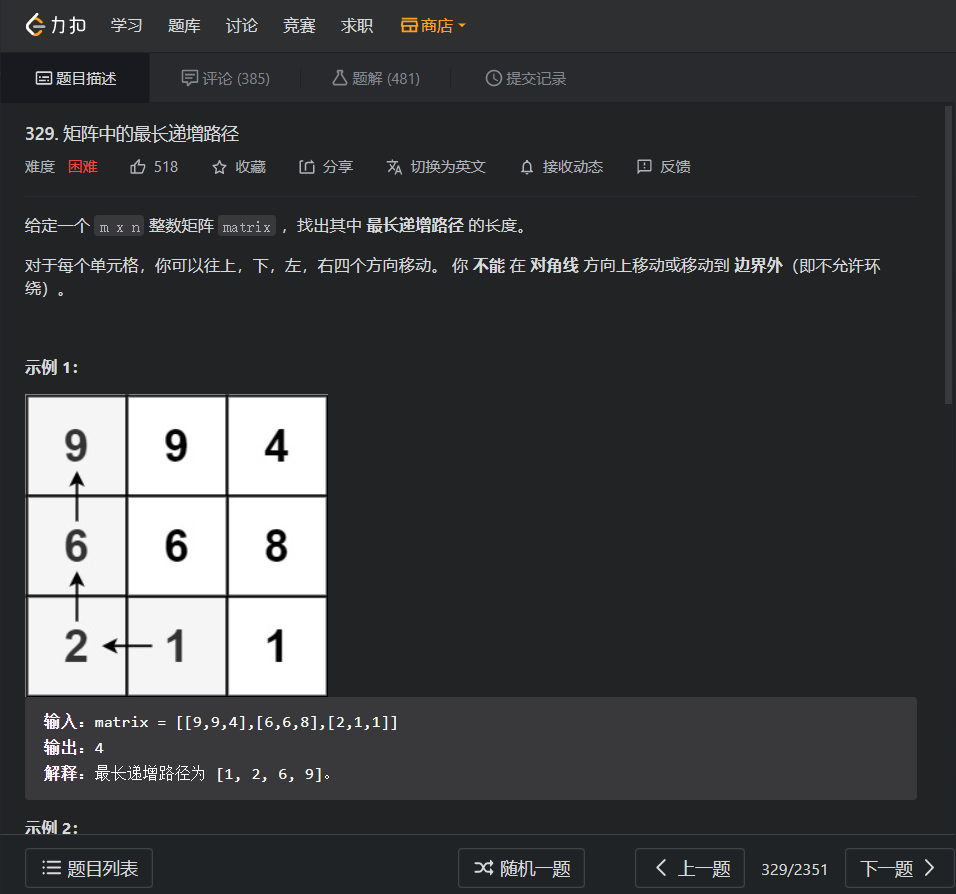
在这里插入图片描述

代码实现（首刷超时 TLE 135/138）

class Solution { 
public:
    int ret;
    void backtracking(vector<vector<int>>& matrix,vector<vector<int>>& visit,int x,int y,int step,int pre)
    { 
        if(x<0 || x>=matrix.size() || y<0 || y>=matrix[0].size() || matrix[x][y] <= pre || visit[x][y])   return;
        int num = 1;
        visit[x][y] = true;
        ret = max(ret,step+1);
        for(int i=0;i<4;++i)
        { 
            if(i<=1)    backtracking(matrix,visit,x+num,y,step+1,matrix[x][y]);
            else    backtracking(matrix,visit,x,y+num,step+1,matrix[x][y]);
            num *= -1;
        }
        visit[x][y] = false;
    }
    int longestIncreasingPath(vector<vector<int>>& matrix) { 
        vector<vector<int>> visit(matrix.size(),vector<int>(matrix[0].size(),false));
        ret = 0;
        for(int x=0;x<matrix.size();++x)
            for(int y=0;y<matrix[0].size();++y)
                backtracking(matrix,visit,x,y,0,-1);
        return ret;
    }
};

代码实现（首刷自解回溯法DFS+记忆化）

class Solution { 
public:
    int ret;
    int backtracking(vector<vector<int>>& matrix,vector<vector<bool>>& visit,vector<vector<int>>& dp,int x,int y,int step,int pre)
    { 
        if(x<0 || x>=matrix.size() || y<0 || y>=matrix[0].size() || matrix[x][y] <= pre || visit[x][y])   return 0;
        if(dp[x][y] > 1)    return dp[x][y];
        int num = 1,tmp = 0;
        visit[x][y] = true;
        for(int i=0;i<4;++i)
        { 
            if(i<=1)    tmp = max(backtracking(matrix,visit,dp,x+num,y,step+1,matrix[x][y]),tmp);
            else   tmp = max(backtracking(matrix,visit,dp,x,y+num,step+1,matrix[x][y]),tmp);
            num *= -1;
        }
        dp[x][y] = max(dp[x][y],tmp+1);
        ret = max(ret,dp[x][y]);
        visit[x][y] = false;
        return tmp+1;
    }
    int longestIncreasingPath(vector<vector<int>>& matrix) { 
        vector<vector<bool>> visit(matrix.size(),vector<bool>(matrix[0].size(),false));
        vector<vector<int>> dp(matrix.size(),vector<int>(matrix[0].size(),1));
        ret = 0;
        for(int x=0;x<matrix.size();++x)
            for(int y=0;y<matrix[0].size();++y)
                if(dp[x][y] == 1) backtracking(matrix,visit,dp,x,y,0,-1);
        return ret;
    }
};