leetcode 518. Coin Change 2 | 518. 零钱兑换 II（暴力递归-＞傻缓存-＞动态规划）-蒲公英云

leetcode 518. Coin Change 2 | 518. 零钱兑换 II（暴力递归-＞傻缓存-＞动态规划）

题目

https://leetcode.com/problems/coin-change-2/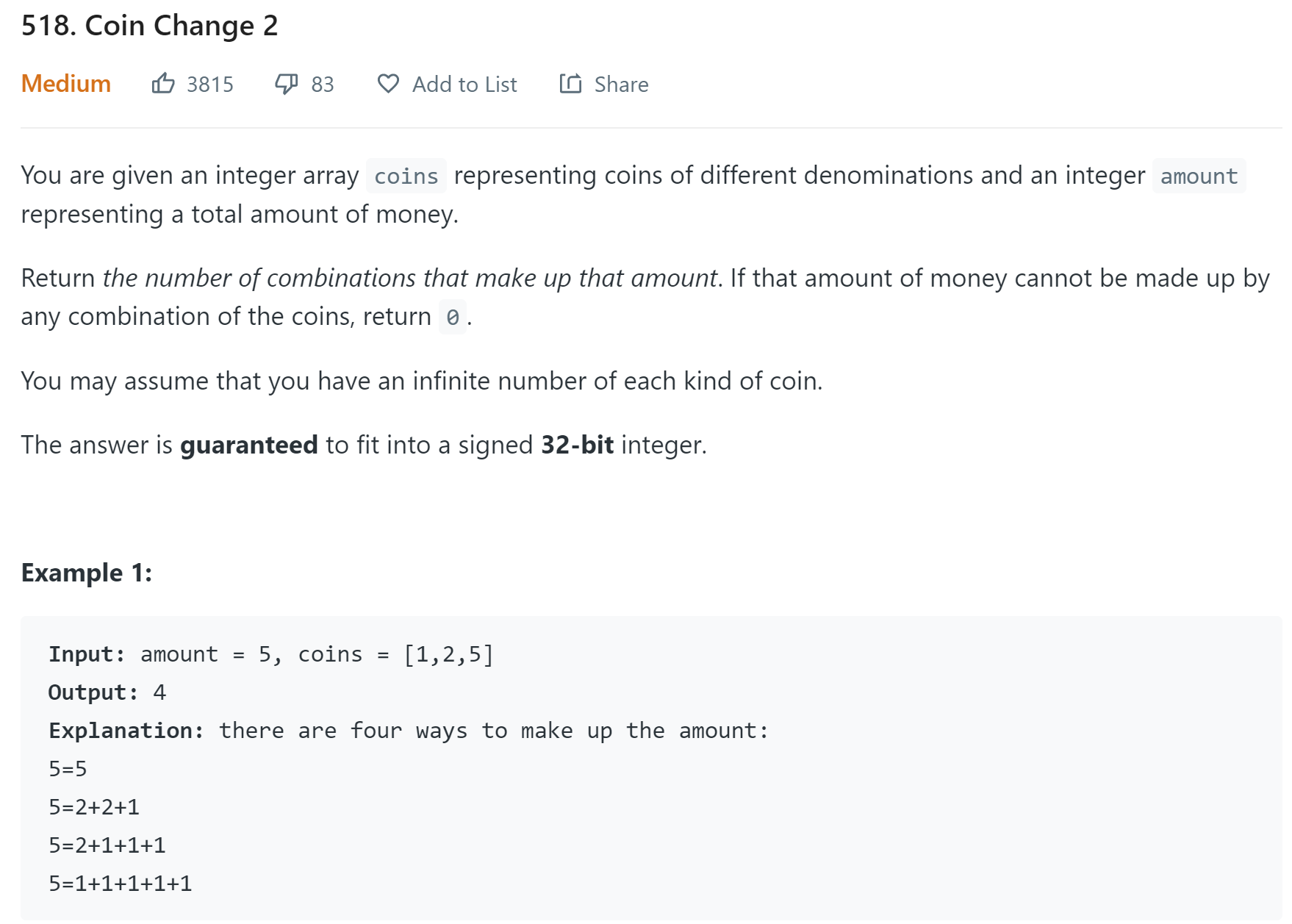
在这里插入图片描述

题解

本题和 leetcode 377. Combination Sum IV | 377. 组合总和 Ⅳ（动态规划）有点像，只不过 377 是不考虑顺序的（排列），本题是考虑顺序的（组合）

而本题与 leetcode 39. Combination Sum | 39. 组合总和（回溯）的区别是，39 题仅有有限个 coin 可用，而本题的 coins 是没有数量限制的。

1、暴力递归（TLE）

先用简单的“尝试”的方法，即递归的方法。
递归函数返回当目标是target时，返回有多少种组合方式。

class Solution { 
    public int change(int amount, int[] coins) { 
        return process(coins, 0, amount);
    }
    // 当目标是target时，返回有多少种组合方式。
    // i表示当前可用的硬币位置，大于等于位置i的硬币可用，避免1+2与2+1重复。
    public int process(int[] coins, int i, int target) {  
        if (target == 0) return 1;
        if (target < 0) return 0;
        int count = 0;
        for (int j = i; j < coins.length; j++) { 
            count += process(coins, j, target - coins[j]);
        }
        return count;
    }
}

在这里插入图片描述

2、傻缓存，记忆化搜索（AC）

给递归函数加个傻缓存，避免重复计算。

自顶（递归入口）向下（basecase）的 带有傻缓存的递归，叫记忆化搜索。
自底（basecase）向上（递归入口）填写 结构化表格，叫动态规划。动态规划的目标，即最终要返回的坐标，就是递归入口的参数对应的坐标。

class Solution { 
    int N;
    public int change(int amount, int[] coins) { 
        N = coins.length;
        int[][] dp = new int[N][amount + 1];
        for (int[] d : dp) { 
            Arrays.fill(d, -1);
        }
        return process(coins, 0, amount, dp);
    }
    // 当目标是target时，返回有多少种组合方式。
    // i表示当前可用的硬币位置，大于等于位置i的硬币可用，避免1+2与2+1重复。
    public int process(int[] coins, int i, int target, int[][] dp) { 
        if (target == 0) return 1;
        if (target < 0) return 0;
        if (dp[i][target] != -1) return dp[i][target];
        int count = 0;
        for (int j = i; j < N; j++) { 
            count += process(coins, j, target - coins[j], dp);
        }
        dp[i][target] = count;
        return count;
    }
}

在这里插入图片描述

3、DP（AC）

将带有傻缓存的递归，转化成自底向上的 dp。

方法是，先填写 basecase，然后根据 递归函数调用时的参数，确定依赖关系。然后，根据依赖关系的顺序，填写 dp 表。

把带有傻缓存的递归，翻译成 dp 的过程：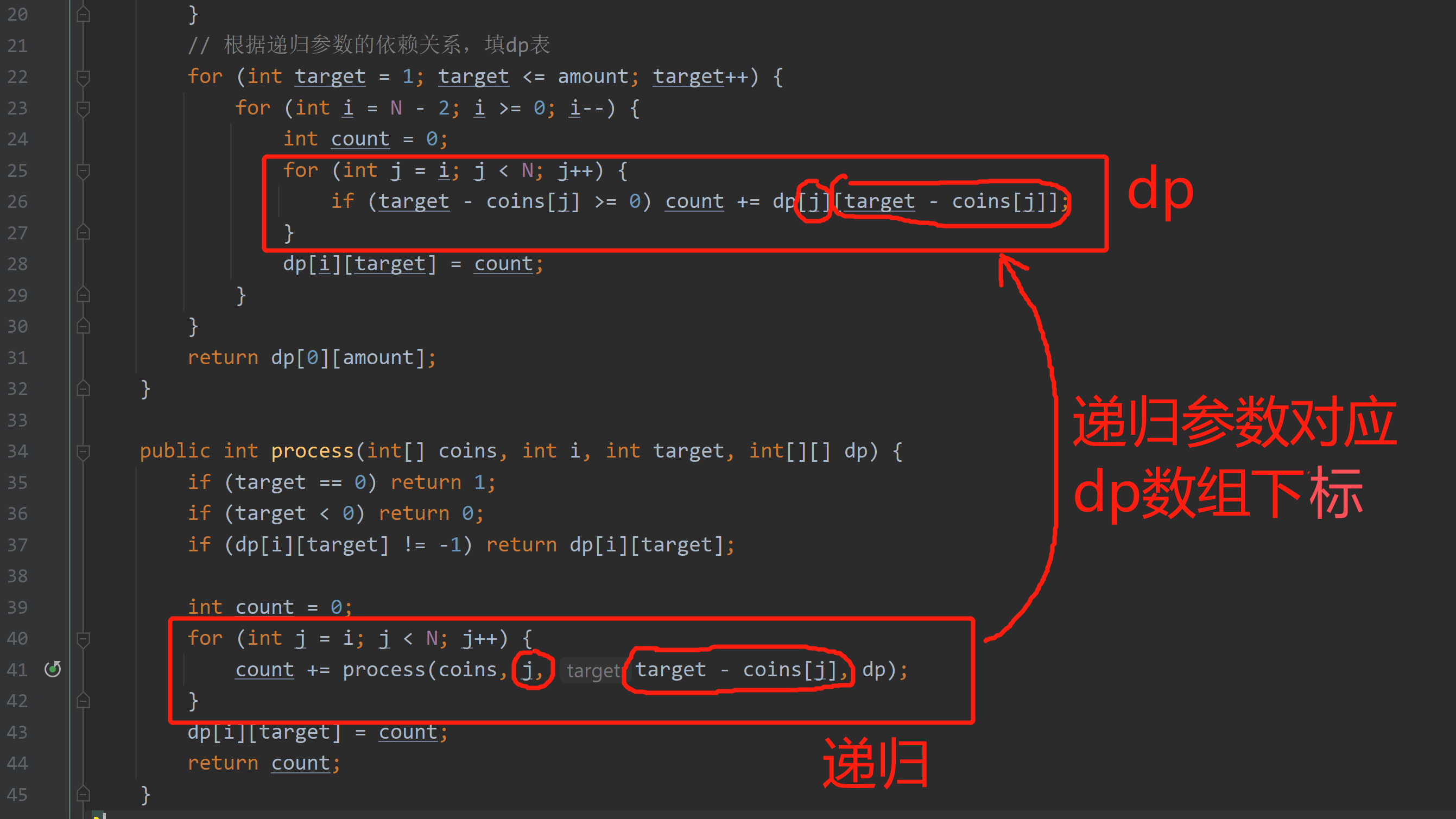
在这里插入图片描述
依赖关系决定填写顺序：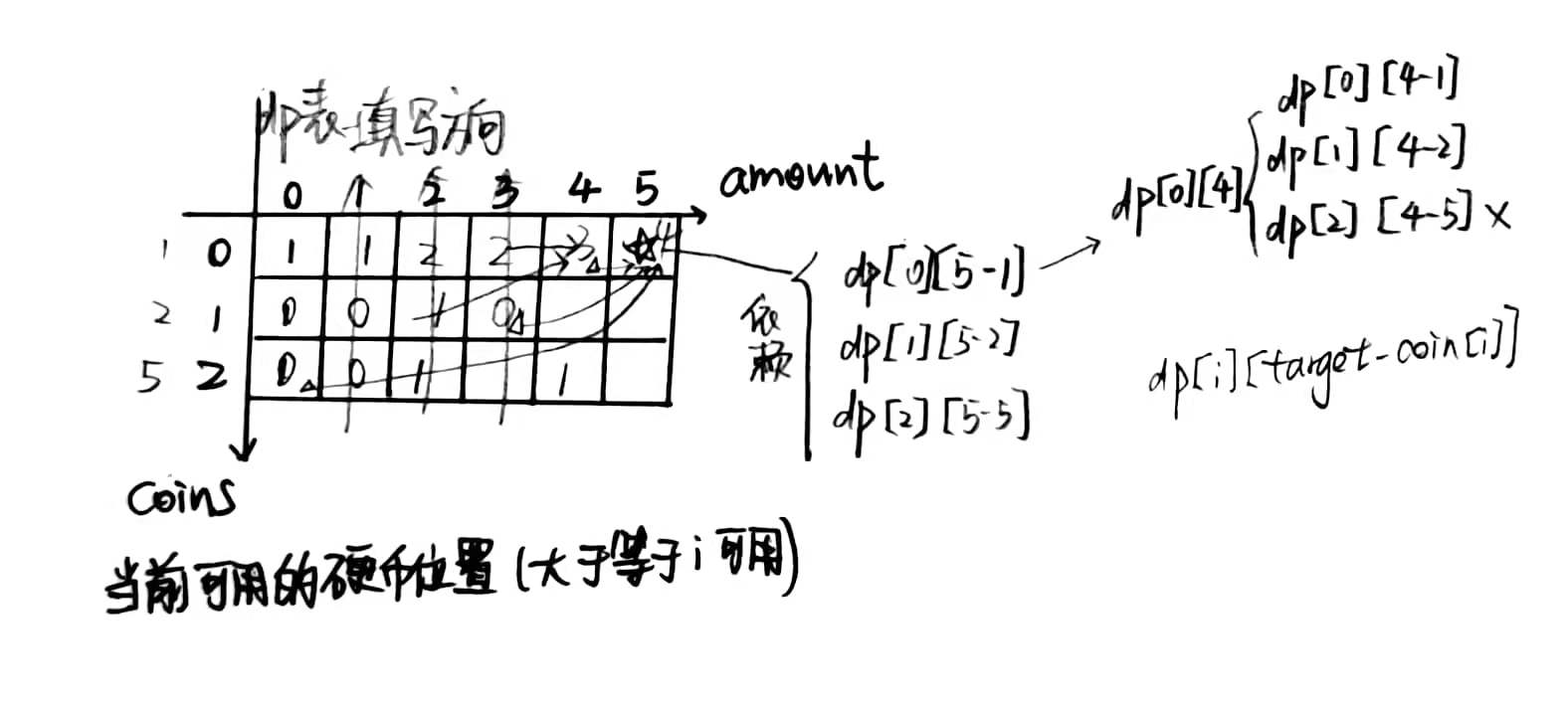

需要注意的是，dp 表是按顺序全部被填满的，有一些没有必要计算的位置也将被计算，而记忆化搜索只计算那些需要依赖的位置。因此，dp 的效率可能会比记忆化搜索更差一些。

class Solution { 
    int N;
    public int change(int amount, int[] coins) { 
        N = coins.length;
        int[][] dp = new int[N][amount + 1];
        for (int[] d : dp) { 
            Arrays.fill(d, -1);
        }
        // base case: 第0列
        for (int i = 0; i < N; i++) { 
            dp[i][0] = 1;
        }
        // base case: 第N-1行
        for (int i = 1; i <= amount; i++) { 
            if (i % coins[N - 1] == 0) dp[N - 1][i] = 1;
            else dp[N - 1][i] = 0;
        }
        // 根据递归参数的依赖关系，填dp表
        for (int target = 1; target <= amount; target++) { 
            for (int i = N - 2; i >= 0; i--) { 
                int count = 0;
                for (int j = i; j < N; j++) { 
                    if (target - coins[j] >= 0) count += dp[j][target - coins[j]];
                }
                dp[i][target] = count;
            }
        }
        return dp[0][amount];
    }
}