330-B树的查询和插入

我就是我 2022-10-05 01:53 77阅读 0赞

## B树的静态索引 ##

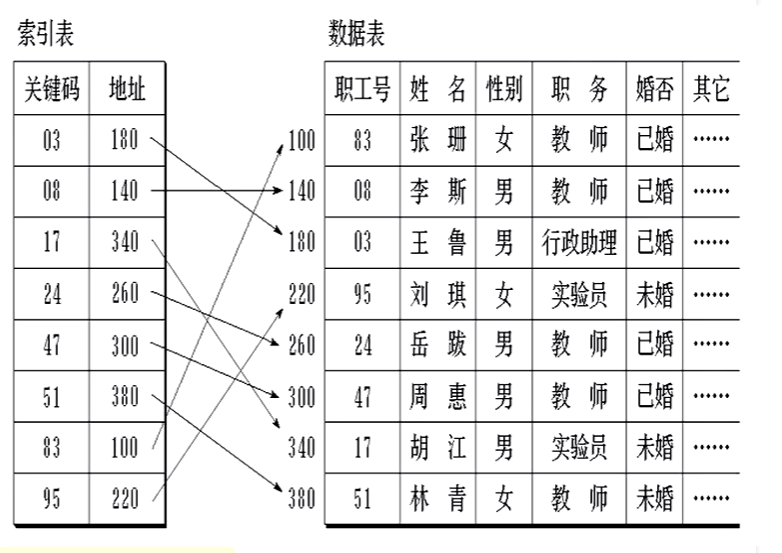
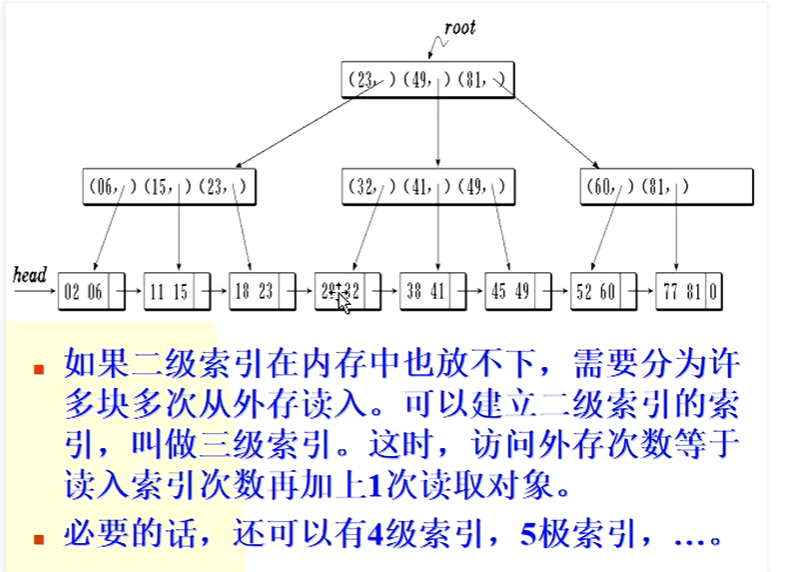
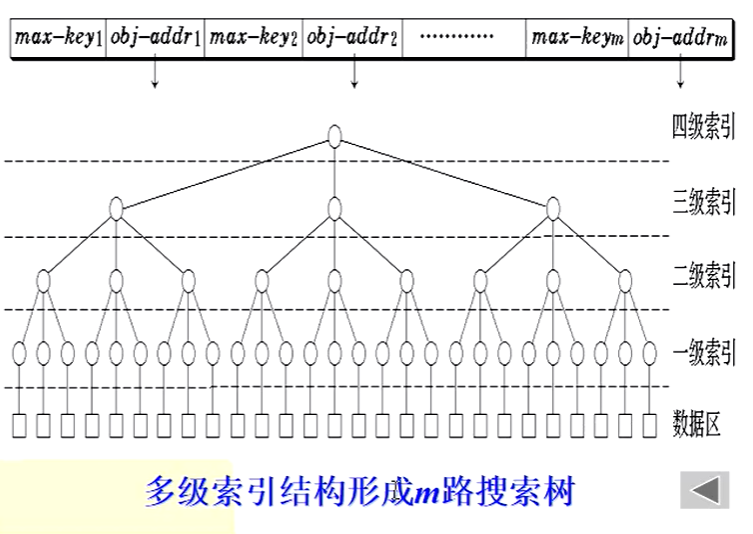
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 1]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 2]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 3]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 4]

## 动态搜索结构 ##

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 5]  
**n是当前结点关键码的个数**  
Ki代表多个关键码，从小到大排序。  
**如果P1有子树，子树的所有关键码均大于K2小于K2。**  
**子树的特点：**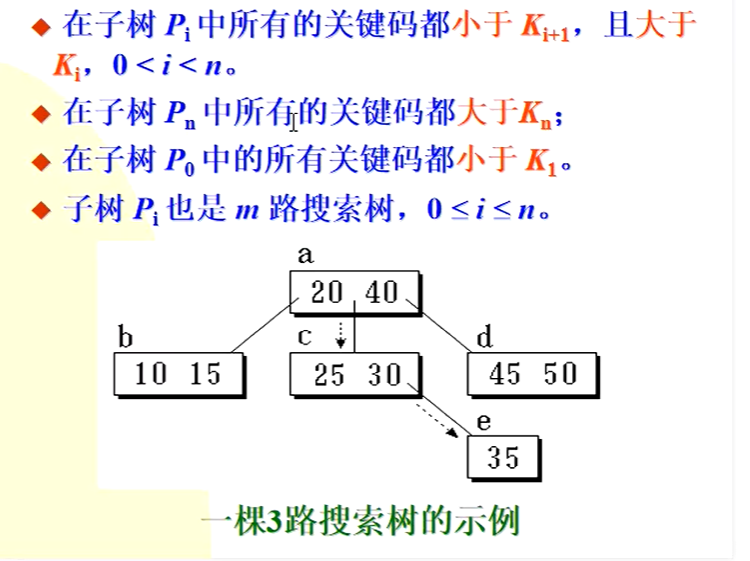  
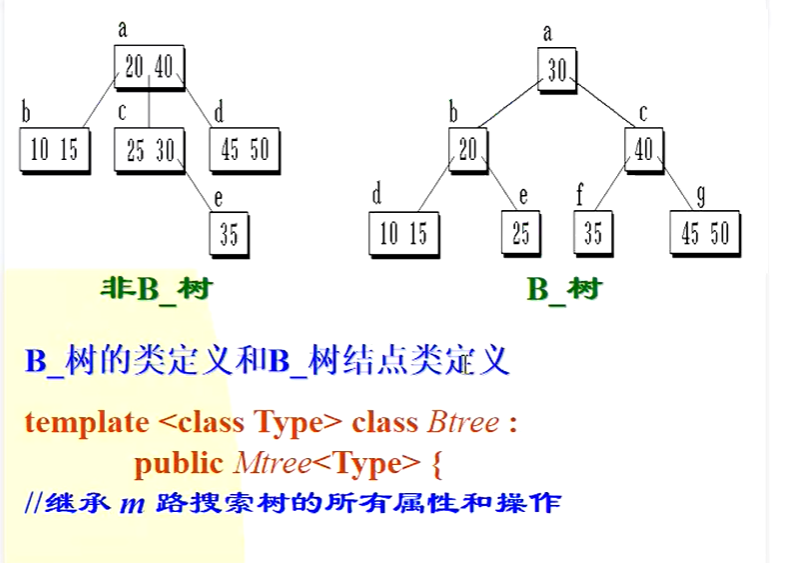
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 6]

## 如何建立B树 ##

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 7]  
**（自平衡树）**  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 8]  
**B树的结点结构**  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 9]  
data的下标1,2，3,4，用于存放数据，0下标是哨兵位，5下标用于分裂  
data下标1,2，3,4的存放的关键码依次增大  
sub分枝的下标0，1,2，3,4，用于存放分枝

**可以看做二叉树。上面的数据（关键码）代表双亲。其关键码大于左孩子而小于右孩子**  
**相当于二叉排序树**  
**如果有左分枝，必要有右分枝。关键码的左右都必须要有分枝**  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 10]

#include<iostream>
    using namespace std;
    
    #define M 5 //分路数
    #define MINITEM (M/2) // 最小分枝数 >=2
    #define MAXITEM (M-1) //最大分枝数
    
    typedef char KeyType;
    typedef struct {
        } Record;//记录集
    typedef struct
    {
        
    	KeyType key;//关键码
    	Record* recptr;//元素类型
    }ElemType;// key_value
    
    struct BNode
    {
        
    	int num;//元素的个数
    	BNode* parent;//双亲的指针
    	ElemType data[M + 1];//元素的个数，相当于下标0,1,2,3,4,5,0下标是哨兵位，5下标是分裂用的
    	BNode* sub[M + 1];//分枝数，0,1,2,3,4,5
    };//B树的结点结构
    
    typedef struct
    {
        
    	BNode* root;//根节点
    	int cursize;//当前B树的结点个数
    }BTree;
    
    BNode* Buynode()//购买节点
    {
        
    	BNode* s = (BNode*)malloc(sizeof(BNode));
    	if (s == nullptr) exit(1);
    	memset(s, 0, sizeof(BNode));
    	return s;
    }
    void Freenode(BNode* p)//释放结点
    {
        
    	free(p);
    }

## 建立B树图(查询，创建） ##

**n是元素的个数，p代表双亲**  
**d是data,s是sub**  
**购买的结点构造如下**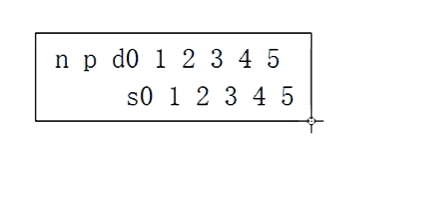  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 11]  
**d是key\_value，s是分枝**

**如果我们进行数据的插入  
不断插入下列数据**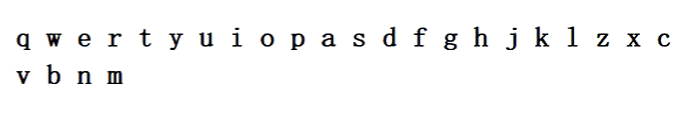  
![在这里插入图片描述][20210605190841876.png_pic_center]  
我们先插入g，是空树，购买一个结点，g插入到data的1号位置。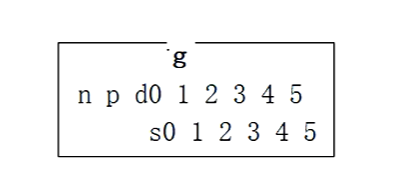  
![在这里插入图片描述][20210605191018496.png_pic_center]  
我们插入k，要先进行查询，树中有没有这个k，所以查询就是首先把k放到哨兵位（d\[0\])，进行查询，拿k和g比较，k>g，在1号位置之后插入，也就是插入到2号位置。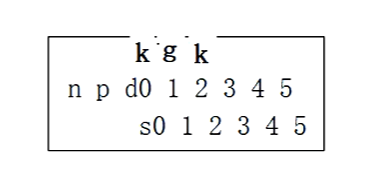  
![在这里插入图片描述][20210605191202254.png_pic_center]

当前，我们的个数是2，最大个数不能超过4。现在是OK的。  
我们接着插入数据m，首先把m放到哨兵位，因为当前个数是2，所以从2下标开始比较，m大于k，我们把m放在3号位置。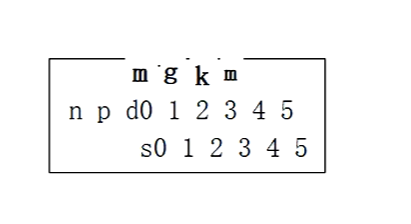  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 12]  
我们再接着插入o，首先把o放到哨兵位，因为当前个数是3，所以从3号位置进行比较，o大于m，o放到4号位置，当前个数就是4了。n=4。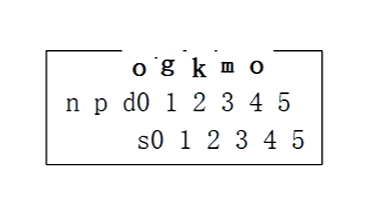  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 13]  
如果我们接着要插入e，把e放入哨兵位，因为当前个数是4，从4号位置开始和o比较，小于o,m,k,g,然后e和e相等，停下来了。我们看s0分枝空不空，如果不空，在分枝下面查，如果是空，则没有查到，e在0位置之后（1号位置）插入，其他的数据后移，n=5了，超过最大个数了，根节点root指向了当前这个结点（如下图）。要进行分裂了。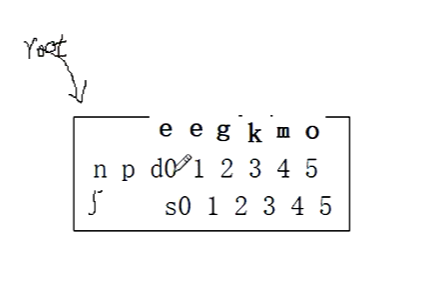  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 14]

**分裂的时候要遵循下面3点**  
![在这里插入图片描述][20210605192138231.png_pic_center]  
首先购买一个节点，从第3位开始，m/2=2,2+1=3。k,m,o移到新节点的0,1,2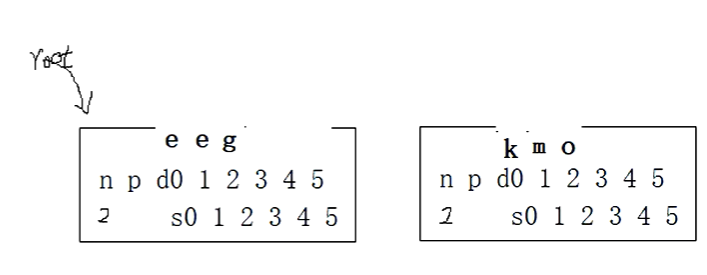  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 15]  
**左右边的数据都是2个。第0里面的不算。  
双亲都为空。  
再购买一个节点作为根节点。  
把k从0位置提到双亲结点的1号位置。  
根节点root指向这个新的双亲结点。**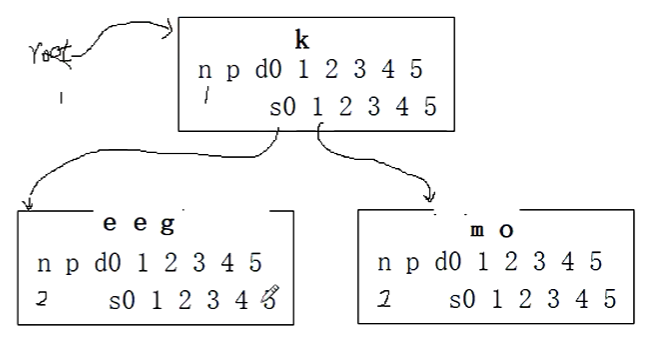  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 16]  
**我们再插入s。首先把s放到哨兵位，**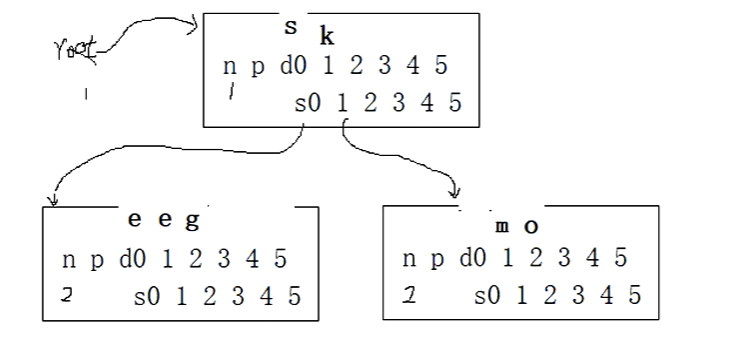  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 17]  
因为当前根节点的个数是1，所以从1号位置开始比较，s大于k，我们看分枝s1空不空，不空，把s再放到哨兵位，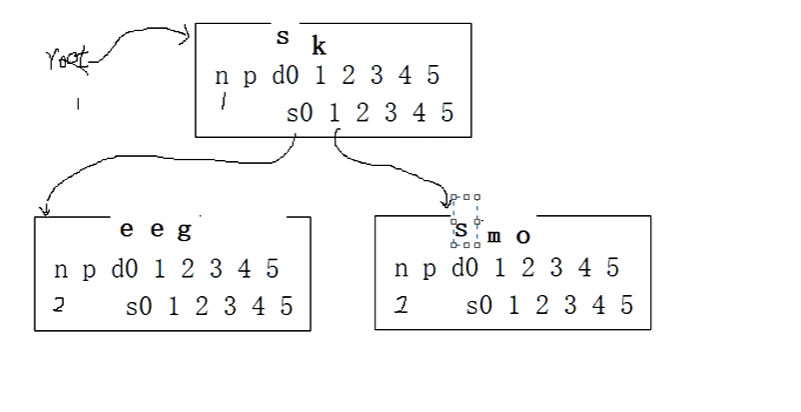  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 18]  
当前节点的元素个数是2，s从2号位置开始进行比较查询，s大于o，在2号位置之后插入数据，当前节点的个数是3。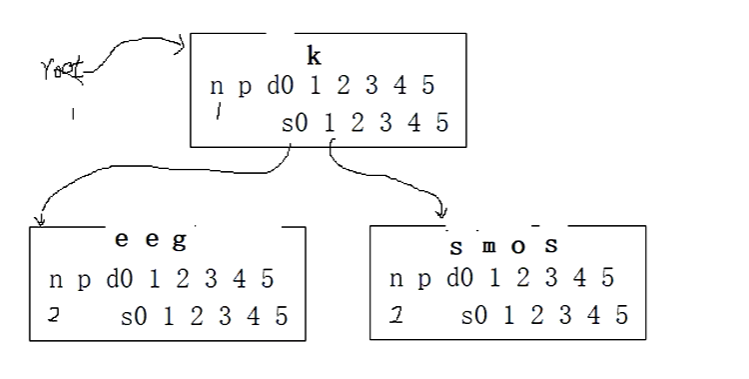  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 19]  
**我们再接着插入a**  
把a放在根节点的哨兵位，当前根节点的个数1，在1号位置比较，a小于k，和0号位置比较，a==a，看s0分枝空不空，不空，把a放在哨兵位，再查找，a小于g,e.等于a。s0是空的，我们把a插入到0位置之后，其他数据后移。当前个数是3。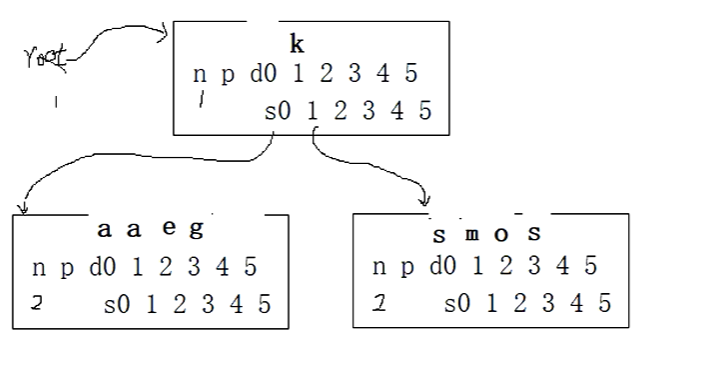  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 20]  
**我们再插入d**，把d放到哨兵位，d小于k，d=d，我们看s0分枝空不空，不空，把d放到哨兵位，d从3位置比较，小于g,e,大于a，我们看分枝s1空不空，空！把数据后移，把d插入到2号位置。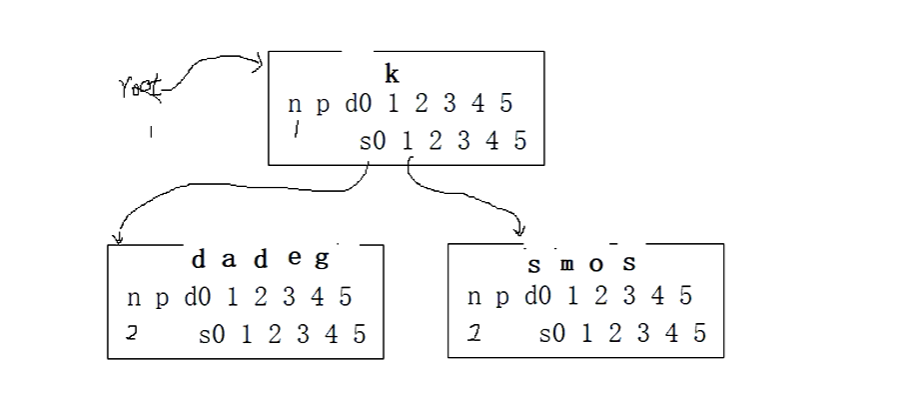  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 21]  
我们再插入f，首先把f放到根节点的哨兵位，f小于k，f=f，在s0里面查询，放到哨兵位，f小于g,大于e，看s3空不空，空的，只能数据后移，f到4号位置。当前个数是5，超出范围，要进行分裂。我们再购买一个节点。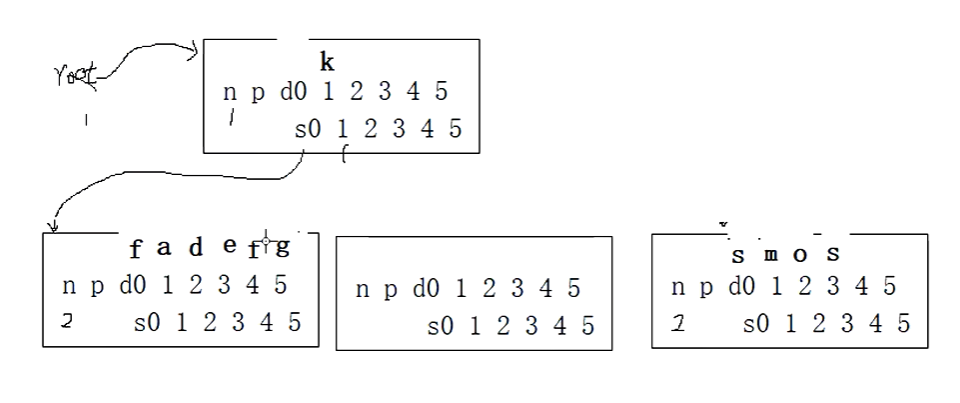  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 22]  
把efg移动到新的节点的0,1，2位置。都是同一个双亲。e给双亲，e和k比较，小于k，e=e，k后移，e在1号位置。然后分枝如下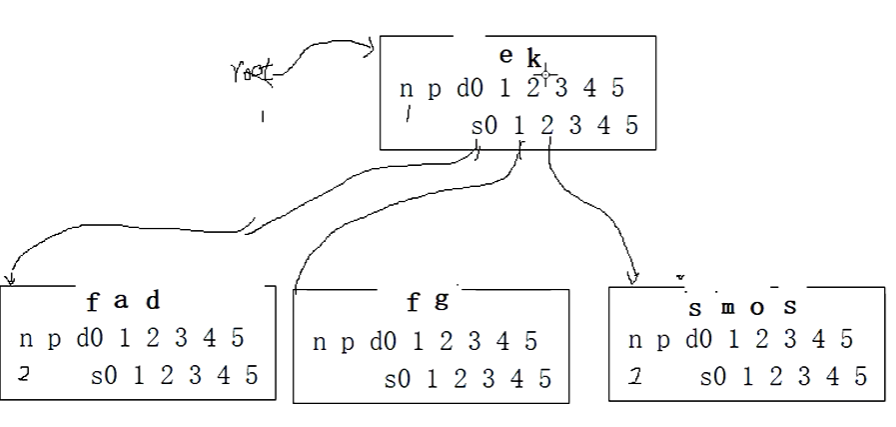  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 23]  
如果我们插入c，c放在根节点的哨兵位，c小于k,e，c=c，s0不空，我们把c再放入哨兵位，查找，小于d，大于a，子树是空，d后移，我们把c插入到2号位置，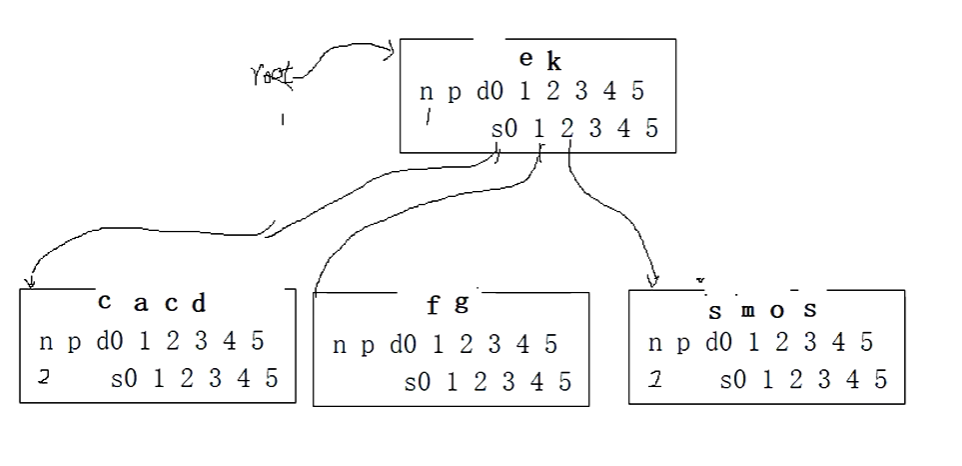  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 24]  
我们插入b，放到根节点的哨兵位进行查询，有2个数据，b小于k,e，b=b，我们看s0不空，放到哨兵位查询，b小于d,c,大于a，子树为空，c和d后移，在2号位置插入b，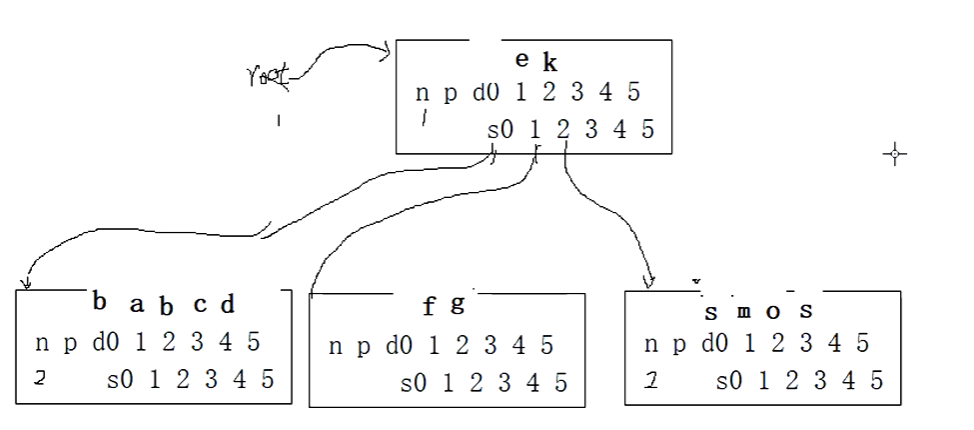  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 25]  
我们再次插入数据h。  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 26]  
我们插入q，放到根节点的哨兵位，大于k，从s2查询，放到哨兵位，q小于s，大于o，s往后移，q放在3号位置。变成4个数据了。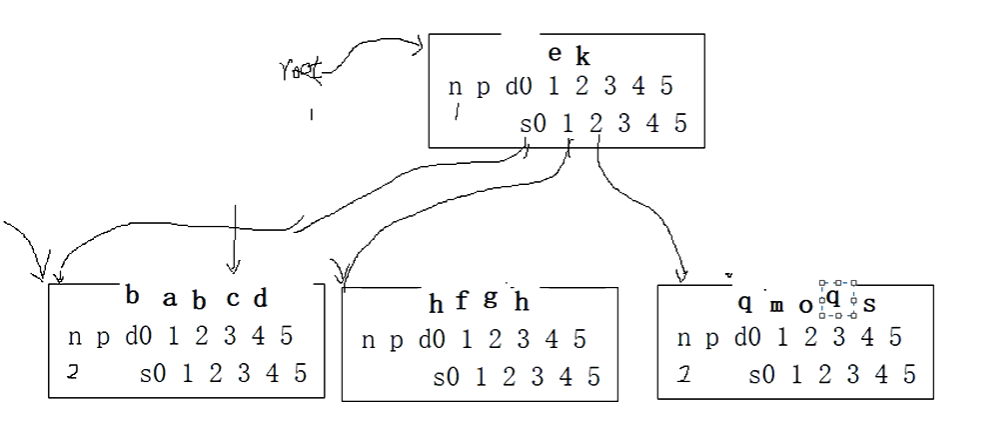  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 27]  
我们再插入p，p大于k，和s比较，小于s,q，大于o，q,s后移，p放在3号位置，变成5个数据了。超出范围，进行分裂，购买一个兄弟结点。pqs移动到新结点的0，1,2，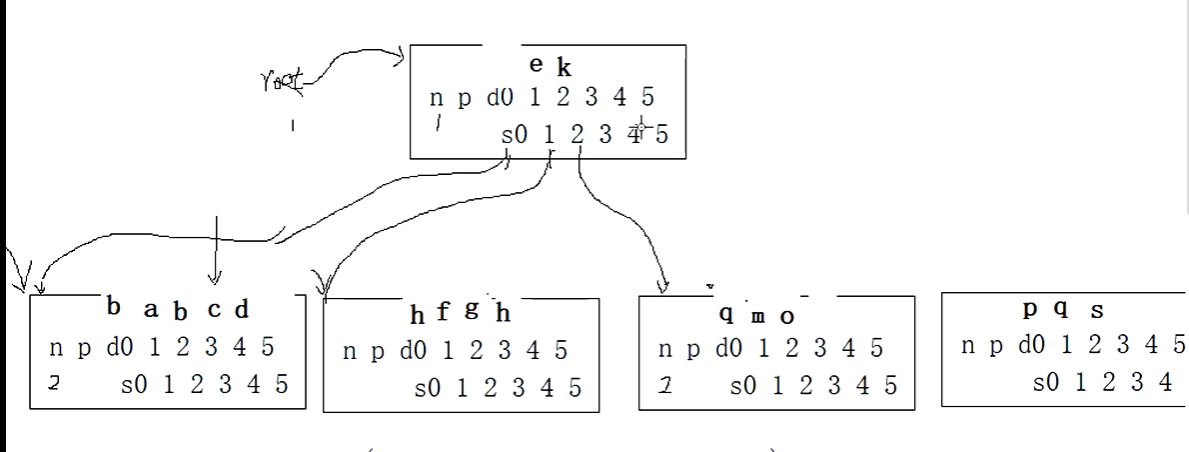  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 28]  
我们把p往双亲走，大于k，p放在3号位置。  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 29]  
3结点4分枝。  
我们再插入j，小于p,k,大于e，是s1分枝找，j大于h，放在4号位置。当前4个数据。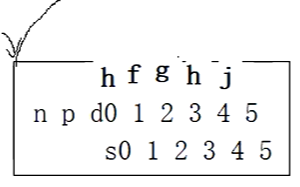  
![在这里插入图片描述][20210605201546546.png_pic_center]  
我们插入i，i小于p,k，i大于e,在s1查询，小于j，大于h，插入，已经5个数据了，要分裂。所以购买一个兄弟结点。hij移动到新结点的0,1，2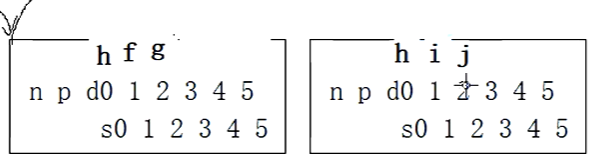  
![在这里插入图片描述][20210605201709168.png_pic_center]  
**把h给双亲，小于p，k,大于e，k,p后移，sub也移动，4个数据5分枝。**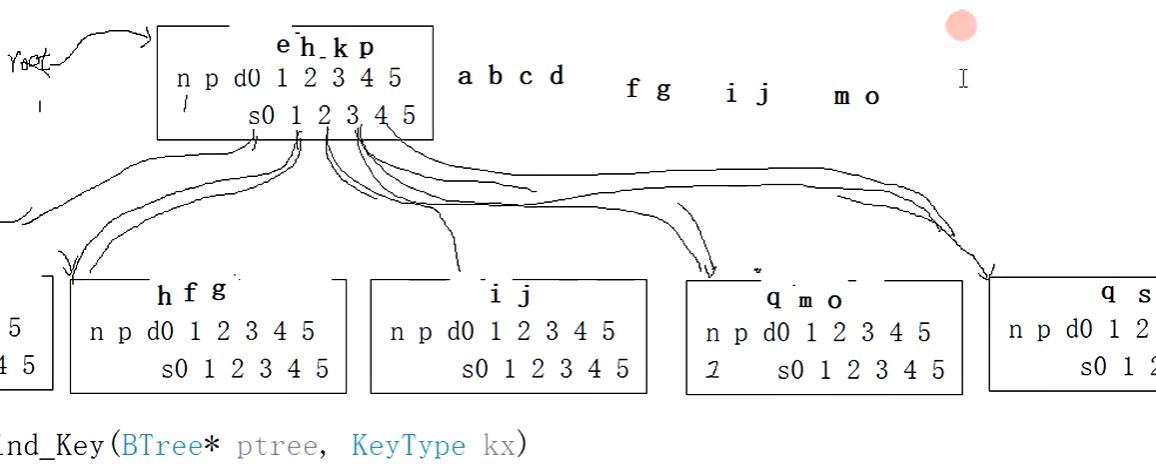  
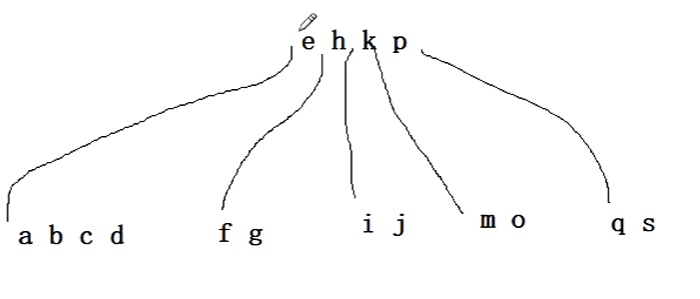
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 30]  
**等价下图**  
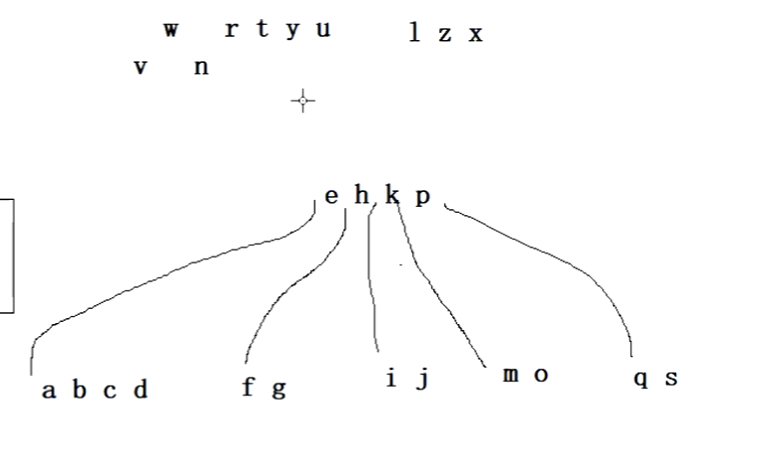
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 31]

## 连级分裂 ##

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 32]  
我们再插入z，大于p，走到s4的地方，大于s，插入s后面。  
我们再插入x，大于p，走到s4的地方，小于z，大于s，插入进来。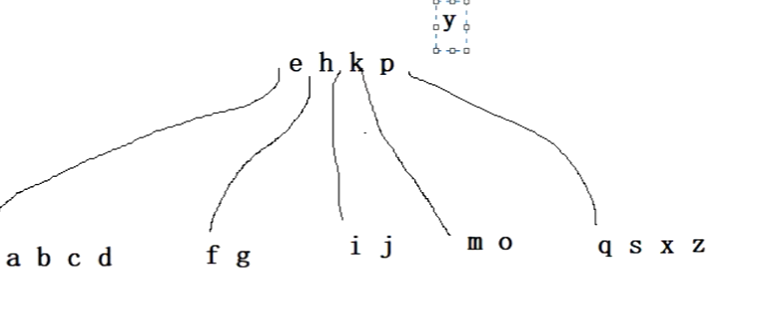  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 33]  
**我们再插入y，大于p，走到s4的地方，小于z大于x，插入，超过了最大元素的个数，要分裂，把xyz放到新结点的0,1，2，把x提到双亲，放在p的后面，5个数据6个分枝，根超出了！！！**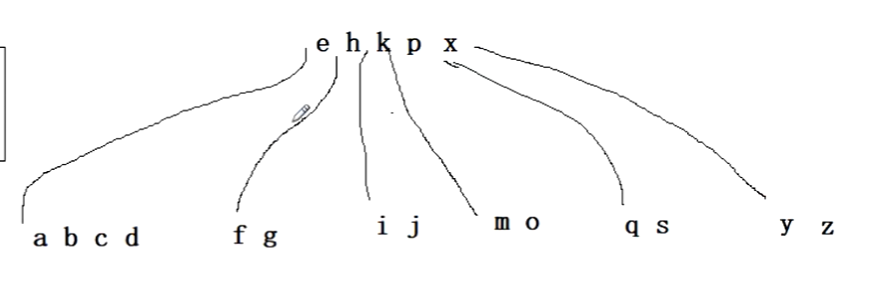  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 34]  
我们再购买结点，我们把k,p,x放到新结点的0,1，2，3数据3分枝。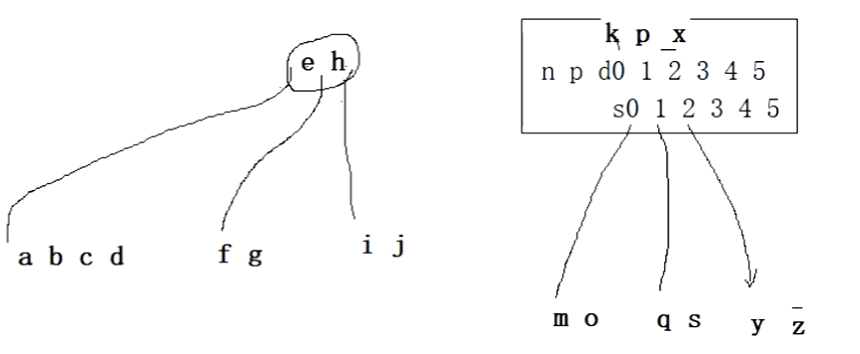  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 35]  
双亲为空，再建立一个结点，k放上去，在1位置，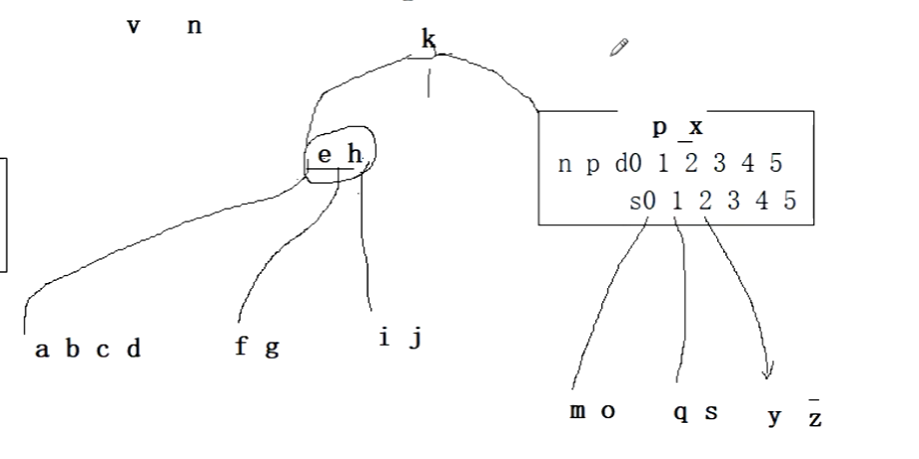  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 36]

## B树的found查询函数 ##

typedef struct
    {
        
    	BNode* pnode;//指向一个结点
    	int index;//查找的结点在哪个位置
    	bool tag;//true;//false
    }Result;
    
    Result Find_Key(BTree* ptree, KeyType kx)
    {
        
    	Result res = {
         nullptr,-1,false };//初始化
    	BNode* p = ptree->root;
    	while (p != nullptr)
    	{
        
    		p->data[0].key = kx;
    		int i = p->num;
    		while (kx < p->data[i].key) --i;
    		res.pnode = p;
    		res.index = i;
    		if (i > 0 && kx == p->data[i].key)
    		{
        
    			res.tag = true;
    			break;
    		}
    		p=p->sub[i];
    	}
    	return res;
    }

## B树的初始化，插入函数 ##

void Init_BTree(BTree* ptree)
    {
        
    	assert(ptree != nullptr);
    	ptree->root = nullptr;
    	ptree->cursize = 0;
    }
    void Insert_Item(BNode* ptr, int pos, ElemType item, BNode* right)
    {
        
    	for (int i = ptr->num; i > pos; --i)
    	{
        
    		ptr->data[i + 1] = ptr->data[i];
    		ptr->sub[i + 1] = ptr->sub[i];
    	}
    	ptr->data[pos + 1] = item;
    	ptr->sub[pos + 1] = right;
    	if (right != nullptr) right->parent = ptr;
    	ptr->num + -1;
    }
    ElemType Move_Right(BNode* ptr, BNode* right)
    {
        
    	for (int j = 0, i = MINITEM + 1; i <= ptr->num; ++i, ++j)
    	{
        
    		right->data[j] = ptr->data[i];
    		right->sub[j] = ptr->sub[i];
    		if (right->sub[j] != nullptr)
    		{
        
    			right->sub[j]->parent = right;
    		}
    	}
    	ptr->num = MINITEM;
    	right->num = MINITEM;
    	right->parent = ptr->parent;
    	return right->data[0];
    }
    BNode* MakeRoot(BNode* left, BNode* right, ElemType item)
    {
        
    	BNode* newroot = Buynode();
    	newroot->data[1] = item;
    	newroot->sub[0] = left;
    	if (left != nullptr) left->parent = newroot;
    	newroot->sub[1] = right;
    	if (right != nullptr) right->parent = newroot;
    	newroot->num = 1;
    	newroot->parent = nullptr;
    	return newroot;
    }
    
    BNode* Splice(BNode* ptr)
    {
        
    	BNode* right = Buynode();
    	ElemType item = Move_Right(ptr, right);
    	if (ptr->parent == nullptr)
    	{
        
    		return MakeRoot(ptr, right, item);
    	}
    	BNode* pa = ptr->parent;
    	int pos = pa->num;
    	pa->data[0] = item;
    	while (item.key < pa->data[pos].key) --pos;
    
    	Insert_Item(pa, pos, item, right);
    	if (pa->num > MAXITEM)
    	{
        
    		return Splice(pa);
    	}
    	else
    	{
        
    		return nullptr;
    	}
    }
    bool Insert(BTree* ptree, ElemType item)
    {
        
    	assert(ptree != nullptr);
    	if (ptree->root == nullptr)
    	{
        
    		ptree->root = MakeRoot(NULL, NULL, item);
    		return true;
    	}
    	Result res = Find_Key(ptree, item.key);
    	if (res.tag) return false;
    	BNode* p = res.pnode;
    	int pos = res.index;
    	Insert_Item(p, pos, item, nullptr);
    	if (p->num > MAXITEM)
    	{
        
    		BNode* newroot = Splice(p);
    		if (newroot != nullptr)
    		{
        
    			ptree->root = newroot;
    		}
    	}
    	ptree->cursize += 1;
    	return true;
    }

## 书写主函数检测 ##

#include<iostream>
    #include<assert.h>
    using namespace std;
    
    #define M 5 //分路数
    #define MINITEM (M/2) // 最小分枝数 >=2
    #define MAXITEM (M-1) //最大分枝数
    
    typedef char KeyType;
    typedef struct {
        } Record;//记录集
    typedef struct
    {
        
    	KeyType key;//关键码
    	Record* recptr;//元素类型
    }ElemType;// key_value
    
    struct BNode
    {
        
    	int num;//元素的个数
    	BNode* parent;//双亲的指针
    	ElemType data[M + 1];//元素的个数，相当于下标0,1,2,3,4,5,0下标是哨兵位，5下标是分裂用的
    	BNode* sub[M + 1];//分枝数，0,1,2,3,4,5
    };//B树的结点结构
    
    typedef struct
    {
        
    	BNode* root;//根节点
    	int cursize;//当前B树的结点个数
    }BTree;
    
    typedef struct
    {
        
    	BNode* pnode;//指向一个结点
    	int index;//查找的结点在哪个位置
    	bool tag;//true;//false
    }Result;
    
    BNode* Buynode()//购买节点
    {
        
    	BNode* s = (BNode*)malloc(sizeof(BNode));
    	if (s == nullptr) exit(1);
    	memset(s, 0, sizeof(BNode));
    	return s;
    }
    void Freenode(BNode* p)//释放结点
    {
        
    	free(p);
    }
    
    
    Result Find_Key(BTree* ptree, KeyType kx)
    {
        
    	Result res = {
         nullptr,-1,false };//初始化
    	BNode* p = ptree->root;
    	while (p != nullptr)
    	{
        
    		p->data[0].key = kx;
    		int i = p->num;
    		while (kx < p->data[i].key) --i;
    		res.pnode = p;
    		res.index = i;
    		if (i > 0 && kx == p->data[i].key)
    		{
        
    			res.tag = true;
    			break;
    		}
    		p=p->sub[i];
    	}
    	return res;
    }
    
    void Init_BTree(BTree* ptree)
    {
        
    	assert(ptree != nullptr);
    	ptree->root = nullptr;
    	ptree->cursize = 0;
    }
    void Insert_Item(BNode* ptr, int pos, ElemType item, BNode* right)
    {
        
    	for (int i = ptr->num; i > pos; --i)
    	{
        
    		ptr->data[i + 1] = ptr->data[i];
    		ptr->sub[i + 1] = ptr->sub[i];
    	}
    	ptr->data[pos + 1] = item;
    	ptr->sub[pos + 1] = right;
    	if (right != nullptr) right->parent = ptr;
    	ptr->num +=1;
    }
    ElemType Move_Right(BNode* ptr, BNode* right)
    {
        
    	for (int j = 0, i = MINITEM + 1; i <= ptr->num; ++i, ++j)
    	{
        
    		right->data[j] = ptr->data[i];
    		right->sub[j] = ptr->sub[i];
    		if (right->sub[j] != nullptr)
    		{
        
    			right->sub[j]->parent = right;
    		}
    	}
    	ptr->num = MINITEM;
    	right->num = MINITEM;
    	right->parent = ptr->parent;
    	return right->data[0];
    }
    BNode* MakeRoot(BNode* left, BNode* right, ElemType item)
    {
        
    	BNode* newroot = Buynode();
    	newroot->data[1] = item;
    	newroot->sub[0] = left;
    	if (left != nullptr) left->parent = newroot;
    	newroot->sub[1] = right;
    	if (right != nullptr) right->parent = newroot;
    	newroot->num = 1;
    	newroot->parent = nullptr;
    	return newroot;
    }
    
    BNode* Splice(BNode* ptr)
    {
        
    	BNode* right = Buynode();
    	ElemType item = Move_Right(ptr, right);
    	if (ptr->parent == nullptr)
    	{
        
    		return MakeRoot(ptr, right, item);
    	}
    	BNode* pa = ptr->parent;
    	int pos = pa->num;
    	pa->data[0] = item;
    	while (item.key < pa->data[pos].key) --pos;
    
    	Insert_Item(pa, pos, item, right);
    	if (pa->num > MAXITEM)
    	{
        
    		return Splice(pa);
    	}
    	else
    	{
        
    		return nullptr;
    	}
    }
    bool Insert(BTree* ptree, ElemType item)
    {
        
    	assert(ptree != nullptr);
    	if (ptree->root == nullptr)
    	{
        
    		ptree->root = MakeRoot(NULL, NULL, item);
    		ptree->cursize+=1;
    		return true;
    	}
    	Result res = Find_Key(ptree, item.key);
    	if (res.tag) return false;
    	BNode* p = res.pnode;
    	int pos = res.index;
    	Insert_Item(p, pos, item, nullptr);
    	if (p->num > MAXITEM)
    	{
        
    		BNode* newroot = Splice(p);
    		if (newroot != nullptr)
    		{
        
    			ptree->root = newroot;
    		}
    	}
    	ptree->cursize += 1;
    	return true;
    }
    
    int main()
    {
        
    	char str[] = {
         "qwertyuiopasdfghjklkzxcvbnm" };
    	int len = strlen(str);
    	BTree myt;
    	Init_BTree(&myt);
    	for (int i = 0; i < len; ++i)
    	{
        
    		ElemType item = {
         str[i],nullptr };
    		cout << Insert(&myt, item);
    	}
    	Result res = Find_Key(&myt, 'x');
    	return 0;
    
    }

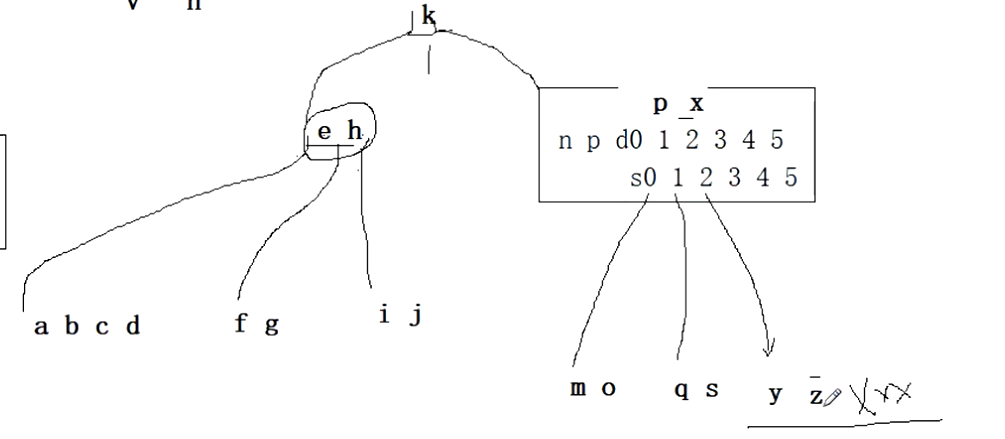
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 37]

## B树的中序遍历 ##

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 38]  
**中序遍历**  
**abcdefghijkmopqsxyz**  
**2数据3分枝**

void InOrder(BNode* p)
    {
        
    	if (p == nullptr) return;
    	InOrder(p->sub[0]);
    	for (int i = 1; i <= p->num; ++i)
    	{
        
    		cout << p->data[i].key << " ";
    		InOrder(p->sub[i]);
    	}
    }
    void Inorder_BTree(BTree* ptree)
    {
        
    	assert(ptree != nullptr);
    	InOrder(ptree->root);
    	cout << endl;
    }

**主函数如下**

int main()
    {
        
    	char str[] = {
         "qwertyuiopasdfghjklkzxcvbnm" };
    	int len = strlen(str);
    	BTree myt;
    	Init_BTree(&myt);
    	for (int i = 0; i < len; ++i)
    	{
        
    		ElemType item = {
         str[i],nullptr };
    		cout << Insert(&myt, item);
    	}
    	Inorder_BTree(&myt);
    	Result res = Find_Key(&myt, 'x');
    	return 0;
    }

**运行截图如下**

![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 39]

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center]: /images/20221005/f8dbae588b19499a90978f6b0c8f8097.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 1]: /images/20221005/b852d9afd92144978eaeaa9893d94bcf.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 2]: /images/20221005/8fac0e9879de407aba956dabdb57ab77.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 3]: /images/20221005/2e2273f6377045988e94174311b2fb88.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 4]: /images/20221005/16aab355c61f4e58a9fd37ab7f8e5f0e.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 5]: /images/20221005/2ec2e24ff44a4c42b91aedb4a0d764ce.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 6]: /images/20221005/d5e3ae8881c84fb9964a3ed49b07703d.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 7]: /images/20221005/0039d506c0024aa8a1b89e94a700e2b8.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 8]: /images/20221005/bd27cb799e5c47c9934f98c57984f000.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 9]: /images/20221005/d743fbf49500425498bd7ea3ba091c9c.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 10]: /images/20221005/64a6b82e6aa1464c932e654ca590e9bd.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 11]: /images/20221005/cd9e76adf05c40bcad7f614a9d424c61.png
[20210605190841876.png_pic_center]: /images/20221005/2cb95dfa6ca741a8ab39f5e973f9f9b0.png
[20210605191018496.png_pic_center]: /images/20221005/7cde2960824a41ecafcb1e1c6b0bca02.png
[20210605191202254.png_pic_center]: /images/20221005/475968e99a9a4cb2bbe3b7ed6d620446.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 12]: /images/20221005/1cb62cdf4239406c92486d2120b6468f.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 13]: /images/20221005/67ddf4d2151d4e4ca48ac71031657504.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 14]: /images/20221005/4b958c92ccfe4d678f9aed2586f5f4e3.png
[20210605192138231.png_pic_center]: /images/20221005/9362825a27b540899b09c14fbc861b7b.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 15]: /images/20221005/e82972b859754af19695ef16e52ce117.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 16]: /images/20221005/f2dcf69b8a914d80bce54edb857305e2.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 17]: /images/20221005/d8ef4f48c2314356be2bb18c2ac9943d.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 18]: /images/20221005/3e64c9cefec5461fbfe2ef045409a756.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 19]: /images/20221005/88cf833268d14ee6aa0260af48aa1b67.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 20]: /images/20221005/1e1d52094914427a81f90100093aa4a7.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 21]: /images/20221005/f68d84ab7e6d4cc9b98486103560dadf.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 22]: /images/20221005/4e96d62296484d53b9ee813a4aa60220.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 23]: /images/20221005/44a9d48cbabd4533baed75216042d485.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 24]: /images/20221005/577a4382d08944f0a0c689a57c057fc6.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 25]: /images/20221005/fc1c86a442a544d7a393c791ddaf0ebc.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 26]: /images/20221005/34efe391a627429282fdc21c13858db8.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 27]: /images/20221005/47756fd028174b57acfa6d4bbb09560e.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 28]: /images/20221005/7e5457aee3e343a0866288c33e72eb7d.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 29]: /images/20221005/dd5e6db5d25148058a0023f96388a5d5.png
[20210605201546546.png_pic_center]: /images/20221005/64f760d528d34705b0e90154542e6047.png
[20210605201709168.png_pic_center]: /images/20221005/55dd56e2bf8e4301a73e1c15abe8615d.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 30]: /images/20221005/a35f3a411b7041709b653b18e7444761.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 31]: /images/20221005/4eea9b04cb54452398de6990f36f2e0a.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 32]: /images/20221005/3d28f0102a9b49d2b8ddf62a565a3672.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 33]: /images/20221005/cf2270d4098c48a0999262aca1e671c8.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 34]: /images/20221005/32a685f86f204a3b91de07f46b33c0a9.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 35]: /images/20221005/2030defa7873486e8ab1b8a90fbf20f7.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 36]: /images/20221005/c16364d745aa411188d28bcf9e8f2c47.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 37]: /images/20221005/90e41ce3c7b446dfbaae29e6f14b1892.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 38]: /images/20221005/815e945dec9949fd9b0461fc1729a53d.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0xJTlpFWVU2NjY_size_16_color_FFFFFF_t_70_pic_center 39]: /images/20221005/b09acc952d994a3d800bbeaaa12cdb95.png