LeetCode - Medium - 99. Recover Binary Search Tree-蒲公英云

Topic

Tree
Depth-first Search

Description

https://leetcode.com/problems/recover-binary-search-tree/

You are given the root of a binary search tree (BST), where exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Follow up: A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

Example 1:

Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Example 2: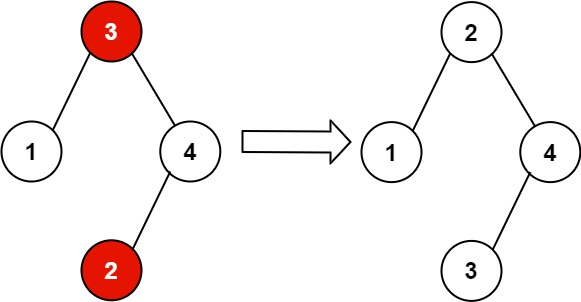

Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.

Constraints:

The number of nodes in the tree is in the range [2, 1000].
− 2 31 < = N o d e . v a l < = 2 31 − 1 -2^{31} <= Node.val <= 2^{31} - 1 −231<=Node.val<=231−1

Analysis

方法一：用到中序遍历模式迭代版，找出相邻前后位置异常两个节点，放入candidates，这种节点最少有2个，最多有4个。然后，在candidates中找出最小值节点和最大值节点。最后，这两最值节点交换值。

方法二：方法一的改进，不用candidates，迭代找出相邻前后位置异常两个节点，取前者为first，后者为second。然后迭代再找出相邻前后位置异常两个节点，然后取小者为second。（这步可能没用到，试想，已排序的数列中，仅相邻一对数交换位置）。最后，first、second互换节点值。

方法三：Morris Traversal。时杂度O(N)，空杂度O(1)，没用到栈。

Submission

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import com.lun.util.BinaryTree.TreeNode;
public class RecoverBinarySearchTree { 
    //方法一：我写的，用到中序遍历模式
    public void recoverTree(TreeNode root) { 
        TreeNode p = root;
        LinkedList<TreeNode> stack = new LinkedList<>();
        List<TreeNode> candidates = new ArrayList<>();
        TreeNode prev = null;
        while(!stack.isEmpty() || p != null) { 
            if(p != null) { 
                stack.push(p);
                p = p.left;
            }else { 
                TreeNode node = stack.pop();
                if(prev != null && prev.val >= node.val) { 
                    candidates.add(prev);
                    candidates.add(node);
                    if(candidates.size() == 4) break;
                }
                prev = node;
                p = node.right;
            }
        }
        TreeNode min = candidates.get(0), max = min;
        for(TreeNode node : candidates) { 
            if(node.val < min.val)
                min = node;
            if(node.val > max.val)
                max = node;
        }
        int temp = min.val;
        min.val = max.val;
        max.val = temp;
    }
    //方法二：方法一的改进
    public void recoverTree2(TreeNode root) { 
        LinkedList<TreeNode> stack = new LinkedList<>();
        TreeNode first = null, second = null;
        TreeNode prev = null, curr = root;
        while(!stack.isEmpty() || curr != null) { 
            if(curr != null) { 
                stack.push(curr);
                curr = curr.left;
            }else { 
                curr = stack.pop();
                if(prev != null && prev.val >= curr.val) { 
                    //incorrect smaller node is always found as prev node
                    if(first == null) 
                        first = prev;
                    //incorrect larger node is always found as curr node
                    second = curr;
                }
                prev = curr;
                curr = curr.right;
            }
        }
        int temp = first.val;
        first.val = second.val;
        second.val = temp;
    }
    // 方法三：Morris遍历算法
    public void recoverTree3(TreeNode root) { 
        TreeNode pre = null;
        TreeNode first = null, second = null;
        // Morris Traversal
        TreeNode temp = null;
        while (root != null) { 
            if (root.left != null) { 
                // connect threading for root
                temp = root.left;
                while (temp.right != null && temp.right != root)
                    temp = temp.right;
                // the threading already exists
                if (temp.right != null) { 
                    if (pre != null && pre.val > root.val) { 
                        if (first == null) { 
                            first = pre;
                        } 
                        second = root;
                    }
                    pre = root;
                    temp.right = null;
                    root = root.right;
                } else { 
                    // construct the threading
                    temp.right = root;
                    root = root.left;
                }
            } else { 
                if (pre != null && pre.val > root.val) { 
                    if (first == null) { 
                        first = pre;
                    } 
                    second = root;
                }
                pre = root;
                root = root.right;
            }
        }
        // swap two node values;
        if (first != null && second != null) { 
            int t = first.val;
            first.val = second.val;
            second.val = t;
        }
    }
}

Test

import static org.junit.Assert.*;
import org.junit.Test;
import com.lun.util.BinaryTree;
import com.lun.util.BinaryTree.TreeNode;
public class RecoverBinarySearchTreeTest { 
    @Test
    public void test() { 
        RecoverBinarySearchTree obj = new RecoverBinarySearchTree();
        TreeNode root1 = BinaryTree.integers2BinaryTree(1,3,null,null,2);
        TreeNode expected1 = BinaryTree.integers2BinaryTree(3,1,null,null,2);
        obj.recoverTree(root1);
        assertTrue(BinaryTree.equals(root1, expected1));
        //---
        TreeNode root2 = BinaryTree.integers2BinaryTree(3,1,4,null,null,2);
        TreeNode expected2 = BinaryTree.integers2BinaryTree(2,1,4,null,null,3);
        obj.recoverTree(root2);
        assertTrue(BinaryTree.equals(root2, expected2));
        //---
        TreeNode root3 = BinaryTree.integers2BinaryTree(3, 9, 6, null, null, 5, 8, null, null, 7, 2);
        TreeNode expected3 = BinaryTree.integers2BinaryTree(3, 2, 6, null, null, 5, 8, null, null, 7, 9);
        obj.recoverTree(root3);
        assertTrue(BinaryTree.equals(root3, expected3));
    }
    @Test
    public void test2() { 
        RecoverBinarySearchTree obj = new RecoverBinarySearchTree();
        TreeNode root1 = BinaryTree.integers2BinaryTree(1,3,null,null,2);
        TreeNode expected1 = BinaryTree.integers2BinaryTree(3,1,null,null,2);
        obj.recoverTree2(root1);
        assertTrue(BinaryTree.equals(root1, expected1));
        //---
        TreeNode root2 = BinaryTree.integers2BinaryTree(3,1,4,null,null,2);
        TreeNode expected2 = BinaryTree.integers2BinaryTree(2,1,4,null,null,3);
        obj.recoverTree2(root2);
        assertTrue(BinaryTree.equals(root2, expected2));
        //---
        TreeNode root3 = BinaryTree.integers2BinaryTree(3, 9, 6, null, null, 5, 8, null, null, 7, 2);
        TreeNode expected3 = BinaryTree.integers2BinaryTree(3, 2, 6, null, null, 5, 8, null, null, 7, 9);
        obj.recoverTree2(root3);
        assertTrue(BinaryTree.equals(root3, expected3));
    }
    @Test
    public void test3() { 
        RecoverBinarySearchTree obj = new RecoverBinarySearchTree();
        TreeNode root1 = BinaryTree.integers2BinaryTree(1,3,null,null,2);
        TreeNode expected1 = BinaryTree.integers2BinaryTree(3,1,null,null,2);
        obj.recoverTree3(root1);
        assertTrue(BinaryTree.equals(root1, expected1));
        //---
        TreeNode root2 = BinaryTree.integers2BinaryTree(3,1,4,null,null,2);
        TreeNode expected2 = BinaryTree.integers2BinaryTree(2,1,4,null,null,3);
        obj.recoverTree3(root2);
        assertTrue(BinaryTree.equals(root2, expected2));
        //---
        TreeNode root3 = BinaryTree.integers2BinaryTree(3, 9, 6, null, null, 5, 8, null, null, 7, 2);
        TreeNode expected3 = BinaryTree.integers2BinaryTree(3, 2, 6, null, null, 5, 8, null, null, 7, 9);
        obj.recoverTree3(root3);
        assertTrue(BinaryTree.equals(root3, expected3));
    }
}