AVL 树

核心

必须保证每个节点左子树和右子树高度差值 <= 1
只有四种旋转（即四种情况）
- 右子树高：
  H（node.right.left） - H（node.right-right） = 1 —> RL 旋转
  H（node.right.right） - H（node.right-left） = 1 —> L 旋转
- 左子树高：
  H（node.left.right） - H（node.left-left） = 1 —> LR 旋转
  H（node.left.left） - H（node.left-right） = 1 —> R 旋转
算法步骤
- 1、从被添加节点，然后一直往上走，直到走到 root
- 2、每次上升到一个节点 node，就比较一下当前节点左子树和右子树的高度，如果满足 |node.left - node.right| > 1 时，就按照上面四种情况判断，到底应该是哪种旋转。
应用场景
- 对插入删除不频繁，只是对查找要求较高，那么AVL还是较优于红黑树。

四种旋转

左子树高
示例：插入 7

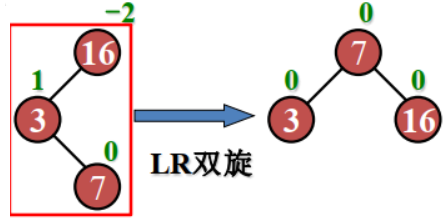
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkzNDYwNw_size_16_color_FFFFFF_t_70

示例：插入 9

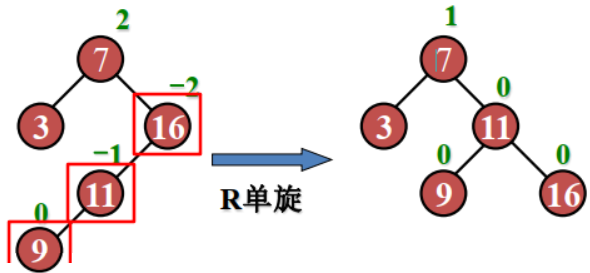
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkzNDYwNw_size_16_color_FFFFFF_t_70 1

右子树高
示例：插入 28

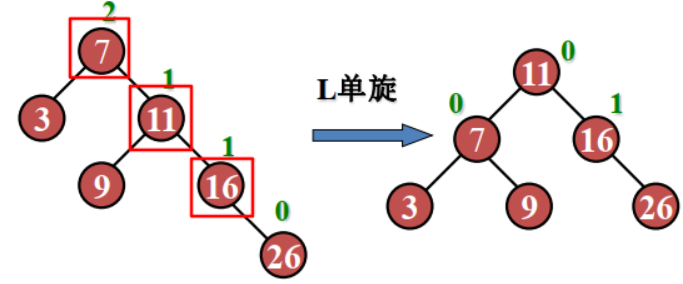
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkzNDYwNw_size_16_color_FFFFFF_t_70 2

示例：插入 18

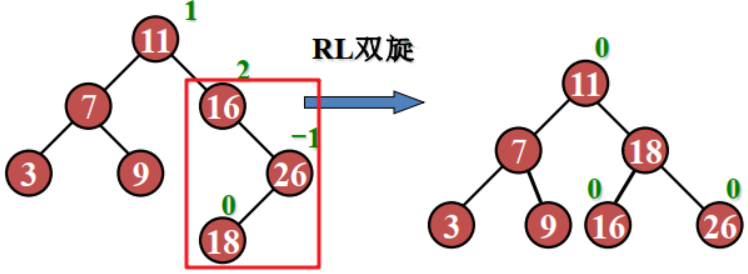
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzkzNDYwNw_size_16_color_FFFFFF_t_70 3

红黑树

核心

两条核心性质
- 两个红色节点不可以连续
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。（叶子节点均指nil叶子）
最后一条性质确保：没有一条路径会比其他路径长出2倍。因而，红黑树是相对接近平衡的二叉树
- 因为每次新插入的一个节点都是红色节点（起始时根节点为黑色），所以只要保证每个父子节点不同时为红色，那么就可以保证每条路径都是红黑节点交替，从而满足任何一个节点到叶节点经过的黑色节点数相同，也保证高度差一定在 2 倍以内。
算法核心
- 每次插入一个节点，把父节点变黑，再把祖父变红，然后把父节点旋转成祖父即可（即此时祖父还是黑色，但不存在冲突了）
- 要解决的问题一：叔叔节点是红色时，无法把祖父变红，不然就红色连续了。
  处理策略：把叔叔一起变黑，再让祖父变为当前节点，然后按照上面的核心思想调整祖父，解决祖父变红的冲突。
- 要解决的第二个问题：红黑树只有 L 旋转与 R 旋转，所以我上面说的把父节点变黑，然后转为祖父的前提必须是，子节点和父节点在同一个方向。
  处理策略：先以父节点进行一次旋转，把插入节点转到同向

应用示例

Linux 进程调度的完全公平调度程序，用红黑树管理进程控制块，进程的虚拟内存区域都存储在一颗红黑树上，每个虚拟地址区域都对应红黑树的一个节点，左指针指向相邻的地址虚拟存储区域，右指针指向相邻的高地址虚拟地址空间;
IO多路复用的epoll的的的实现采用红黑树组织管理的的的sockfd，以支持快速的增删改查;
Java的的的中TreeMap中的中的实现;

算法实现

两种旋转

右旋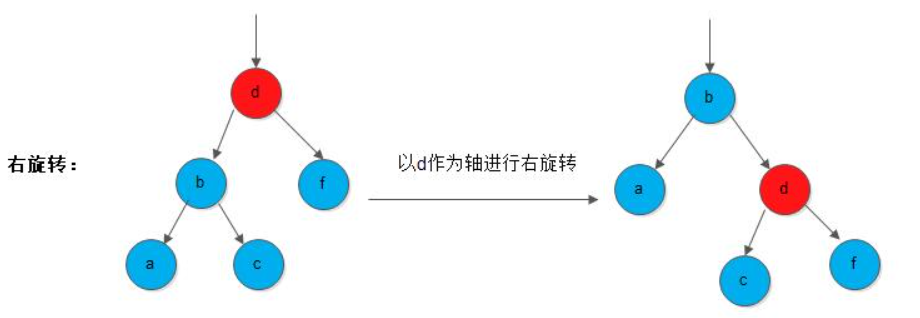
在这里插入图片描述
左旋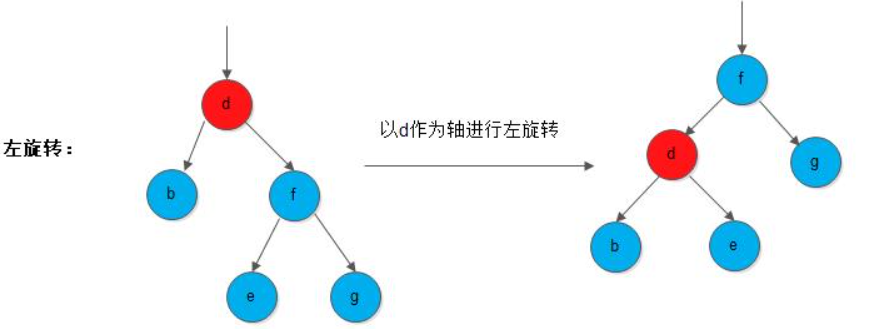

插入的三种情况

case 1： 当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色。

对策：将当前结点的父结点和叔叔结点涂黑，祖父结点涂红，把当前结点指向祖父结点，从新的当前结点重新开始算法

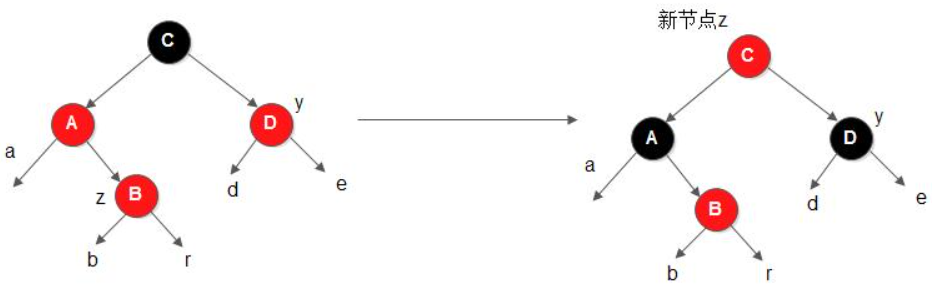
case 2： 当前结点的父结点是红色，叔叔（假设叔叔是祖父的右子）结点是黑色，当前结点是其父结点的右子。

对策：当前结点的父结点做为新的当前结点，以新当前结点为支点左旋

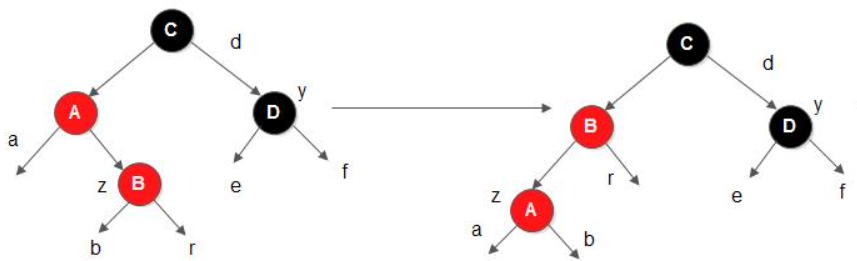
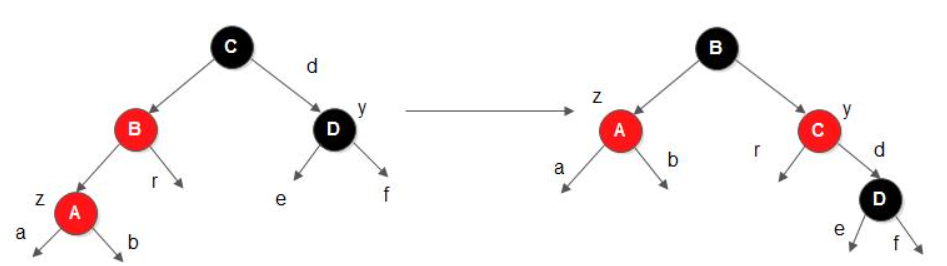
case 3： 当前结点的父结点是红色，叔叔（假设叔叔是祖父的右子）结点是黑色，当前结点是其父结点的左子。

对策：父结点变为黑色，祖父结点变为红色，在祖父结点为支点右旋
最终目的都是转换为这种情况

代码

int rb_insert_fixup(rb_tree_t *root, rb_node_t *node)
{
    rb_node_t *parent;
    rb_node_t *grand_parent;
    //If parent exist, and the color of parent is RED
    while((parent = node->parent) && parent->color == COLOR_RED)
    {
        grand_parent = parent->parent;
        //parent node is grand_parent node's left child(grand_parent should not be NULL, because parent->color==COLOR_RED)
        if(grand_parent->left == parent)
        {
            rb_node_t *uncle = grand_parent->right;
            //Case 1: uncle is RED
            if(uncle && uncle->color == COLOR_RED)
            {
                parent->color = COLOR_BLACK;
                uncle->color = COLOR_BLACK;
                grand_parent->color = COLOR_RED;
                node = grand_parent;
                continue;
            }
            //Case 2: uncle is BLACK, and node is parent's right child
            if(parent->right == node)
            {
                rb_rotate_left(root, parent);
                // reset parent and node pointer
                rb_node_t *tmp;
                tmp = parent;
                parent = node;
                node = tmp;
                //Here successful convert Case 2 to Case3
            }
            //Case 3: uncle is BLACK, and node is parent's left child
            parent->color = COLOR_BLACK;
            grand_parent->color = COLOR_RED;
            rb_rotate_right(root, grand_parent);
        }
        else{
            rb_node_t *uncle = grand_parent->left;
            //Case 1: uncle is RED
            if(uncle && uncle->color == COLOR_RED)
            {
                parent->color = COLOR_BLACK;
                uncle->color = COLOR_BLACK;
                grand_parent->color = COLOR_RED;
                node = grand_parent;
                continue;
            }
            //Case 2: uncle is BLACK, and node is parent's left child
            if(parent->left == node)
            {
            rb_rotate_right(root,parent);
                //reset parent and node pointer
                rb_node_t *tmp;
                tmp = parent;
                parent = node;
                node = tmp;
                //Here success convert Case 2 to Case 3
            }
            //Case 3: uncle is BLACK, and node is parent's right child
            parent->color = COLOR_BLACK;
            grand_parent->color = COLOR_RED;
            rb_rotate_left(root, grand_parent);
        }
    }
    (*root)->color = COLOR_BLACK;
    return 0x0;
}
int insert_rbtree(rb_tree_t *root, rb_node_t *node)
{
    rb_node_t *p = *root;
    rb_node_t *q = NULL;
    //find the position we need to insert
    while(p)
    {
        q = p;
        if(p->key == node->key)
            return 1;
        else if(p->key > node->key)
            p = p->left;
        else
            p = p->right;
    }
    node->parent = q;
    if(q != NULL)
    {
        if(node->key < q->key)
            q->left = node;
        else
            q->right = node;
    }
    else{
        *root = node;
    }
    node->color = COLOR_RED;
    return rb_insert_fixup(root, node);
}

B/B+ 树

B 树相对于上面说的树，核心区别就是多叉

B+ 树的相对于 B 树的核心区别有两点

只有叶子节点保存值
叶子节点间有双向指针

存储引擎使用 B+ 树的原因

只有叶子节点保存值
- 相对于 B 树来说，主文件指针只存放在叶子节点，所以这样的话如果一个索引块可以全部放满的话，那么 B+ 树的节点可以能放的索引项比 B 树多，因为不放行指针或数据值；
- 而且也不会出现查找不同值时，耗费的时间不同。
叶子节点间有双向指针
- B 树没有删除合并，B+ 树通过删除合并来保证每个节点指针的利用率在 50%~100%，逻辑其实很容易相通，就是下层节点个数决定上层节点的个数，所以只要保证了叶子节点的空间利用率，也就保证了整棵树其他节点的空间利用率，删除节点合并就是 B+ 树独创的，每个节点间的双向指针实现的，会根据被删除元素页子节点的剩余元素个数，与相邻页子节点的现存元素个数，来决定是合并还是窃取元素，然后再逐层向上调整指针；
- 也正是这个双向指针还可以方便的范围检索。

（具体插入和删除示例可以参考我数据库的文章：数据库索引之 B+ 树）