LeetCode - Medium - 131. Palindrome Partitioning-蒲公英云

Topic

Dynamic Programming
Backtracking
Depth-first Search

Description

https://leetcode.com/problems/palindrome-partitioning/

Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.

A palindrome string is a string that reads the same backward as forward.

Example 1:

Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]
Example 2:
Input: s = "a"
Output: [["a"]]

Constraints:

1 <= s.length <= 16
s contains only lowercase English letters.

Analysis

思路分析

本题涉及到两个关键问题：

切割问题，有不同的切割方式
判断回文

切割问题类似组合问题。

例如对于字符串abcdef：

组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中在选取第三个…。
切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中在切割第三段…。

切割问题，也可以抽象为一颗树形结构，如图：

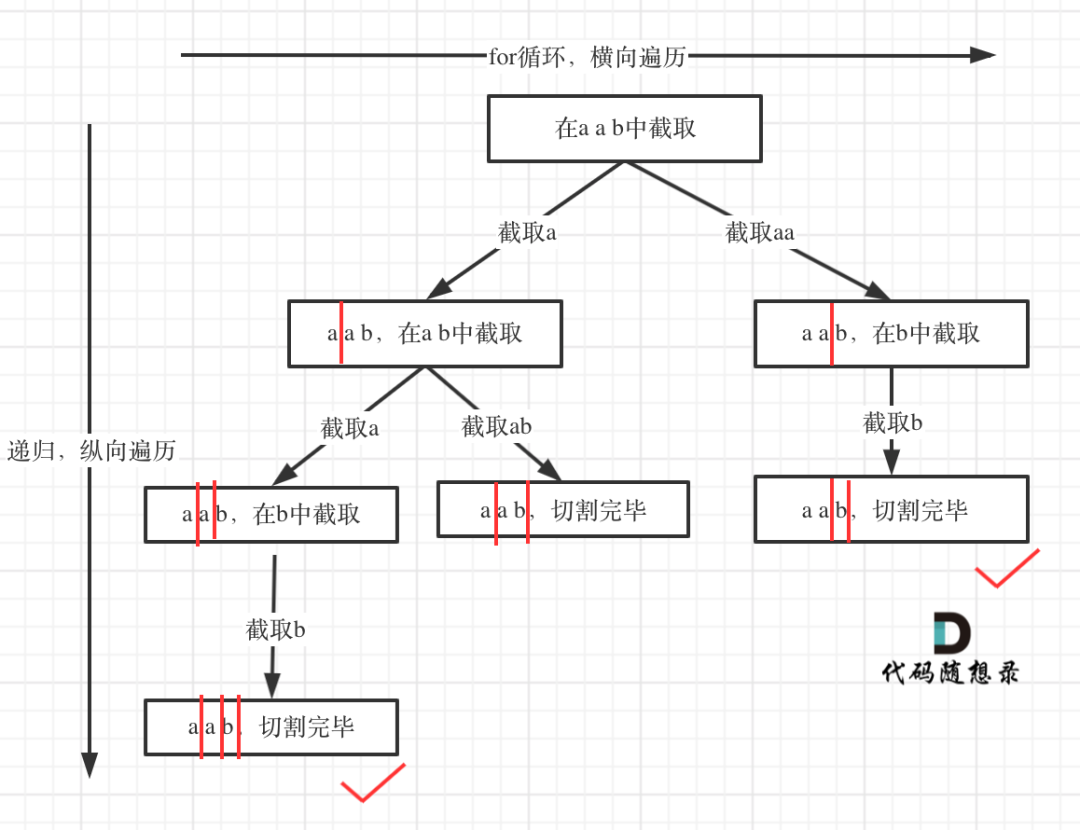
递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。

判读回文

private boolean isPalindrome(String str, int startIndex, int endIndex) { 
    for(endIndex--; startIndex < endIndex; startIndex++, endIndex--) { 
        if(str.charAt(startIndex) != str.charAt(endIndex))
            return false;
    }
    return true;
}

回溯三弄

函数签名

List<String> path：存放切割后回文的子串。
String originalString：一开始传入的字符串
int startIndex：子字符串开始下标。切割过的地方，不能重复切割，和组合问题也是保持一致的。
List<List<String>> result：存放结果集。

代码如下：

private void backtracking(List<String> path, String originalString, //
                    int startIndex, List<List<String>> result) { }

终止条件

从上文树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归终止的终止条件。

代码如下：

if(startIndex >= originalString.length()) { 
    result.add(new ArrayList<>(path));
    return;
}

遍历顺序

首先判断这个子串是不是回文，如果是回文，就加入在用来记录切割过的回文子串的path。

//i 表示终止截断字符的下标（子串不含终止截断字符）
for(int i = startIndex + 1; i <= originalString.length(); i++) { 
    if(isPalindrome(originalString, startIndex, i)) { 
        path.add(originalString.substring(startIndex, i));//加入[startIndex,i]在s中的子串
    }else { 
        continue;
    }
    backtracking(path, originalString, i, result);// 寻找i+1为起始位置的子串
    path.remove(path.size() - 1);
}

最终代码

移步至Submission

参考资料

回溯算法：分割回文串

Submission

public List<List<String>> partition(String s) { 
        List<String> path = new ArrayList<>();
        List<List<String>> result = new ArrayList<>();
        backtracking(path, s, 0, result);
        return result;
    }
    private void backtracking(List<String> path, String originalString, // 
            int startIndex, List<List<String>> result) { 
        if(startIndex >= originalString.length()) { 
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i = startIndex + 1; i <= originalString.length(); i++) { 
            if(isPalindrome(originalString, startIndex, i)) { 
                path.add(originalString.substring(startIndex, i));
            }else { 
                continue;
            }
            backtracking(path, originalString, i, result);
            path.remove(path.size() - 1);
        }
    }
    private boolean isPalindrome(String str, int startIndex, int endIndex) { 
        for(endIndex--; startIndex < endIndex; startIndex++, endIndex--) { 
            if(str.charAt(startIndex) != str.charAt(endIndex))
                return false;
        }
        return true;
    }

Test

import static org.junit.Assert.*;
import java.util.Arrays;
import java.util.List;
import static org.hamcrest.collection.IsIterableContainingInAnyOrder.containsInAnyOrder;
import org.junit.Test;
public class PalindromePartitioningTest { 
    @Test
    @SuppressWarnings("unchecked")
    public void test() { 
        PalindromePartitioning obj = new PalindromePartitioning();
        List<List<String>> actual1 = obj.partition("a");
        // System.out.println(actual1);
        assertThat(actual1, //
                containsInAnyOrder(Arrays.asList("a")));
        List<List<String>> actual2 = obj.partition("aab");
        // System.out.println(actual2);
        assertThat(actual2, //
                containsInAnyOrder(Arrays.asList("aa", "b"), Arrays.asList("a", "a", "b")));
    }
}