排序算法——归并排序
引言
归并排序可以使用递归或迭代的方式来实现,时间复杂度是都是 O(N * logN)。
归并排序的核心是将待排序数组分组,可以整体二分,也可以设置步长迭代切分。归并排序在操作过程中,充分利用了上一次排序的结果,而 O(N ^ 2)的排序算法每次比较都是独立的,简单的说就是,上一次的比较行为完全和下次比较行为无关,这在一定程度上浪费了比较的既得结果。
一、递归实现
不论是递归还是迭代,归并排序最重要的部分是实现两个分组的归并,在归并的过程中同时做好排序。
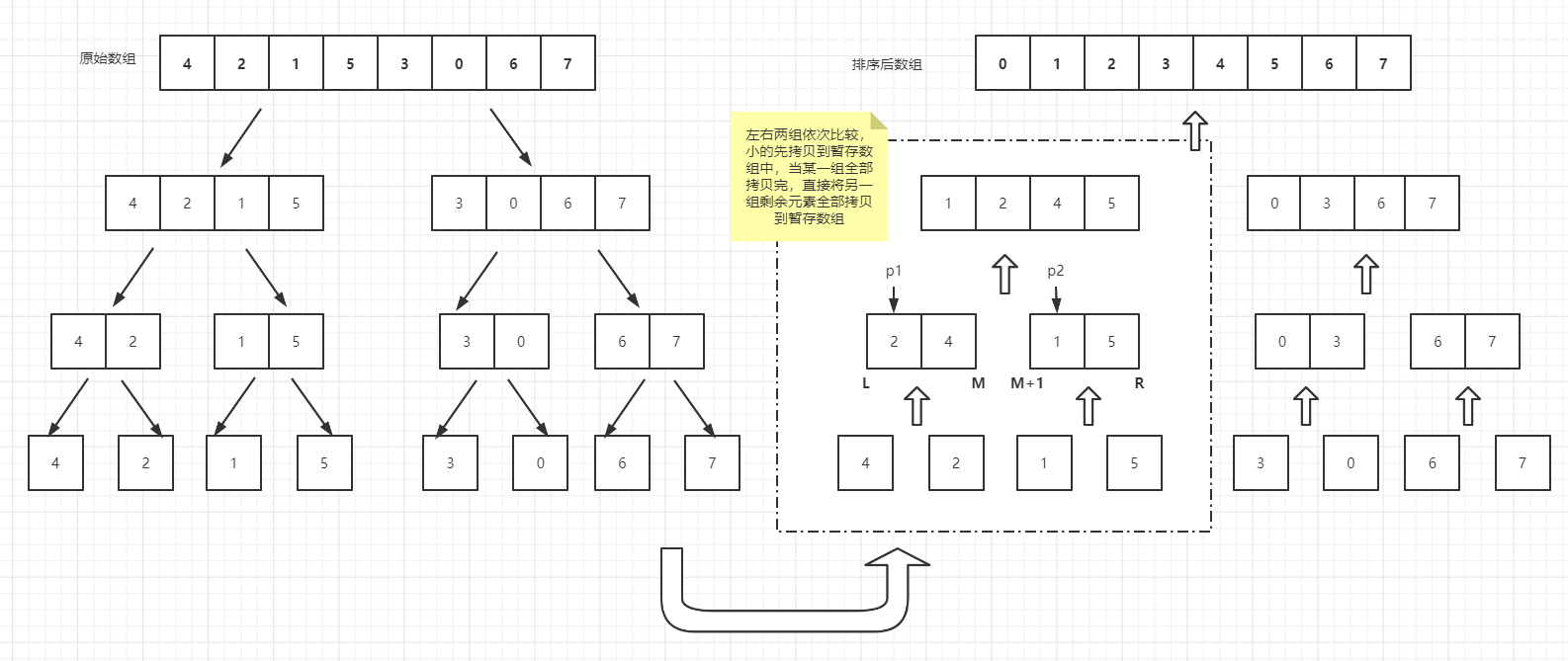
整个过程可以分为两个大的部分:迭代过程、归并过程。
1、迭代的过程,可以简单思考一个操作步骤:将数组二分,然后合并。如果循环二分,那么一定存在一个条件,只剩1个元素,此时无法再继续二分,直接返回:
public static void process(int[] arr, int L, int R) {if (L == R)return;// 防止整型越界的二分方法,逻辑上等同于 (L + R)/2int mid = L + ((R - L) >> 1);process(arr, L, mid);process(arr, mid + 1, R);merge(arr, L, mid, R);}
2、归并的过程,需要一个暂存数组,来存放有序的既得结果,merge(…)方法接收原始数组和 3 个指针,分别是左右两组的外侧边界,以及中点位置。
p1和p2分别指向两组的最左侧,当p1和p2在各自组内未超过最右边界 M 和 R 时,取较小值放入到 help 暂存数组中。当然,左右两组一定会有一个指针先达到最右边界,并由于自加操作跳出第一个 while 循环,而另一个分组还有未拷贝的元素,此时只需要判断哪个分组还有数据,并依次直接拷贝即可,这样就完成了一次归并操作,最后再将暂存数组中排好序的元素放回到原数组即可:
public static void merge(int[] arr, int L, int M, int R) {int[] help = new int[R - L + 1];int i = 0;int p1 = L;int p2 = M + 1;while (p1 <= M && p2 <= R) {help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];}// 要么p1越界了,要么p2越界了while (p1 <= M) {help[i++] = arr[p1++];}while (p2 <= R) {help[i++] = arr[p2++];}for (i = 0; i < help.length; i++) {arr[L + i] = help[i];}}
完整代码如下:
/*** 递归方式** @param arr*/public static void mergeSort(int[] arr) {if (arr == null || arr.length < 2)return;process(arr, 0, arr.length - 1);}public static void process(int[] arr, int L, int R) {if (L == R)return;int mid = L + ((R - L) >> 1);process(arr, L, mid);process(arr, mid + 1, R);merge(arr, L, mid, R);}public static void merge(int[] arr, int L, int M, int R) {int[] help = new int[R - L + 1];int i = 0;int p1 = L;int p2 = M + 1;while (p1 <= M && p2 <= R) {help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];}// 要么p1越界了,要么p2越界了while (p1 <= M) {help[i++] = arr[p1++];}while (p2 <= R) {help[i++] = arr[p2++];}for (i = 0; i < help.length; i++) {arr[L + i] = help[i];}}
二、迭代实现
迭代实现的方式相较于递归的方式要考虑更多的边界条件,归并的过程都是一样的,只是在循环的时候,需要考虑步长的变化,以及剩余元素是否足够分组的问题。
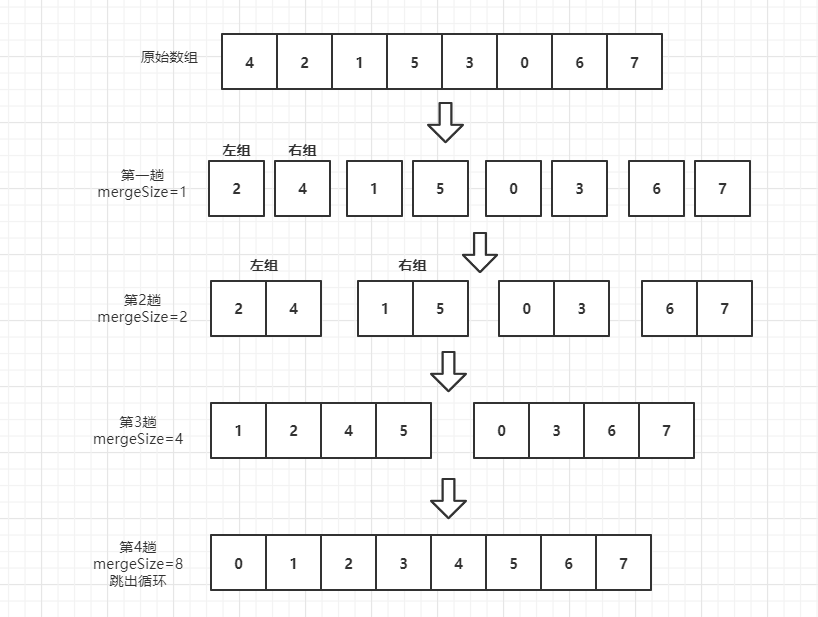
原始数组的长度是关键
以下是完整代码:
/*** 非递归方式*/public static void mergeSort2(int[] arr) {if (arr == null || arr.length < 2)return;int N = arr.length;// 步长,表示的是归并操作一个组里面元素的个数int mergeSize = 1;// 由于归并排序需要分为两组,因此,如果mergeSize>=N,// 那就只有一组或连一组都凑不够,因此就停止mergewhile (mergeSize < N) {int L = 0;while (L < N) {if (mergeSize >= N - L) {break;}int M = L + mergeSize - 1;int R = M + Math.min(mergeSize, N - M - 1);merge(arr, L, M, R);L = R + 1;}// 防止移除if (mergeSize > N / 2)break;// 步长自增2倍mergeSize <<= 1;}}
三、归并排序的时间复杂度
对迭代方式实现的归并排序来说,使用master公式,具备以下时间消耗形式:
T(N) = 2 * T(N/2) + O(N),a = 2,b = 2,d = 1
那么根据 master 公式,因为 logb a = log2 = 1 与 d = 1 相等,因此最终的时间复杂度为:
O(N^d * logN) = O(N * logN)
对迭代方式实现的归并排序来说,步长调整的过程是 1 -> 2 -> 4 -> 8…,当步长超过 N 后即停止增长,因此它的变化次数就是 logN,而相邻两组 merge ,需要将整个数组重新merge一遍。
每次步长调整后都要将整个数组 merge 一遍,因此就是 O(N * logN)。
四、测试与对数器
// for testpublic static int[] generateRandomArray(int maxSize, int maxValue) {int[] arr = new int[(int) ((maxSize + 1) * Math.random())];for (int i = 0; i < arr.length; i++) {arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random());}return arr;}// for testpublic static int[] copyArray(int[] arr) {if (arr == null) {return null;}int[] res = new int[arr.length];for (int i = 0; i < arr.length; i++) {res[i] = arr[i];}return res;}// for testpublic static boolean isEqual(int[] arr1, int[] arr2) {if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) {return false;}if (arr1 == null && arr2 == null) {return true;}if (arr1.length != arr2.length) {return false;}for (int i = 0; i < arr1.length; i++) {if (arr1[i] != arr2[i]) {return false;}}return true;}// for testpublic static void printArray(int[] arr) {if (arr == null) {return;}for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}// for testpublic static void main(String[] args) {int testTime = 500000;int maxSize = 100;int maxValue = 100;System.out.println("测试开始");for (int i = 0; i < testTime; i++) {int[] arr1 = generateRandomArray(maxSize, maxValue);int[] arr2 = copyArray(arr1);mergeSort(arr1);mergeSort2(arr2);if (!isEqual(arr1, arr2)) {System.out.println("出错了!");printArray(arr1);printArray(arr2);break;}}System.out.println("测试结束");}
总结
归并排序通过保留比较结果的方式将 O(N^2)的排序算法时间复杂度提升到了 O(N * logN) 。
merge()方法是归并排序的关键,它的逻辑是将元素分为左右两组,两组元素逐一比较,将小的元素拷贝到临时数组中。
两种方式——递归、迭代,其本质都是从 1 比 1,到 2 比 2,到 4 比 4 …,迭代的方式直接是设置了初始步长为1,而迭代的方式是先将数组层层二分,其实分到最后也一定会出现 1 比 1的情况,即 L == R,再层层返回,实际上也是从 1 比 1开始,再 2 比 2 ,最后整个数组的左右两组做比较进行归并。
递归的方式很明显简化了编码过程,但一定要注意 base case 的返回条件。迭代的方式除了要考虑步长的变化规则,还要分析当数组剩余元素不够左组的情况,需要如何处理,以及在步长 * 2 前先判断是否有越界的风险,因为一旦越界(Integer.maxValue),步长可能会变为负数,造成死循环。

































还没有评论,来说两句吧...