计算机视觉中的深度学习3: 线性分类
Slides:百度云 提取码: gs3n
线性分类的参数
线性分类的公式
f ( x , W ) = W x + b f(x, W) = Wx + b f(x,W)=Wx+b
其中 W W W为参数或者权重
以一个有 10 10 10类的 32 × 32 × 3 32\times 32\times 3 32×32×3的图片为例
其中 f ( x , W ) f(x, W) f(x,W)和 b b b为 ( 10 , ) (10,) (10,)向量, W W W为 ( 10 , 3072 ) (10, 3072) (10,3072)的矩阵, x x x为 ( 3072 , ) (3072,) (3072,)的向量。
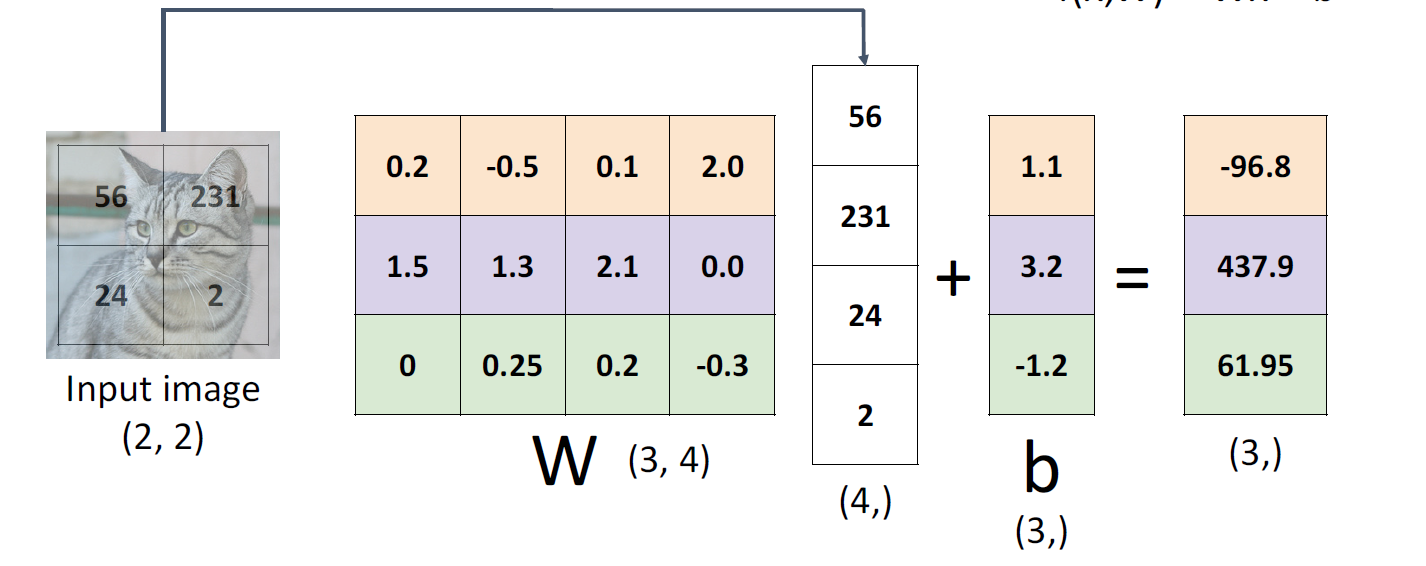
也可以把bias并到Weight里面,就变成如下了
公式也可以简化成
f ( x , W ) = W x f(x, W) = Wx f(x,W)=Wx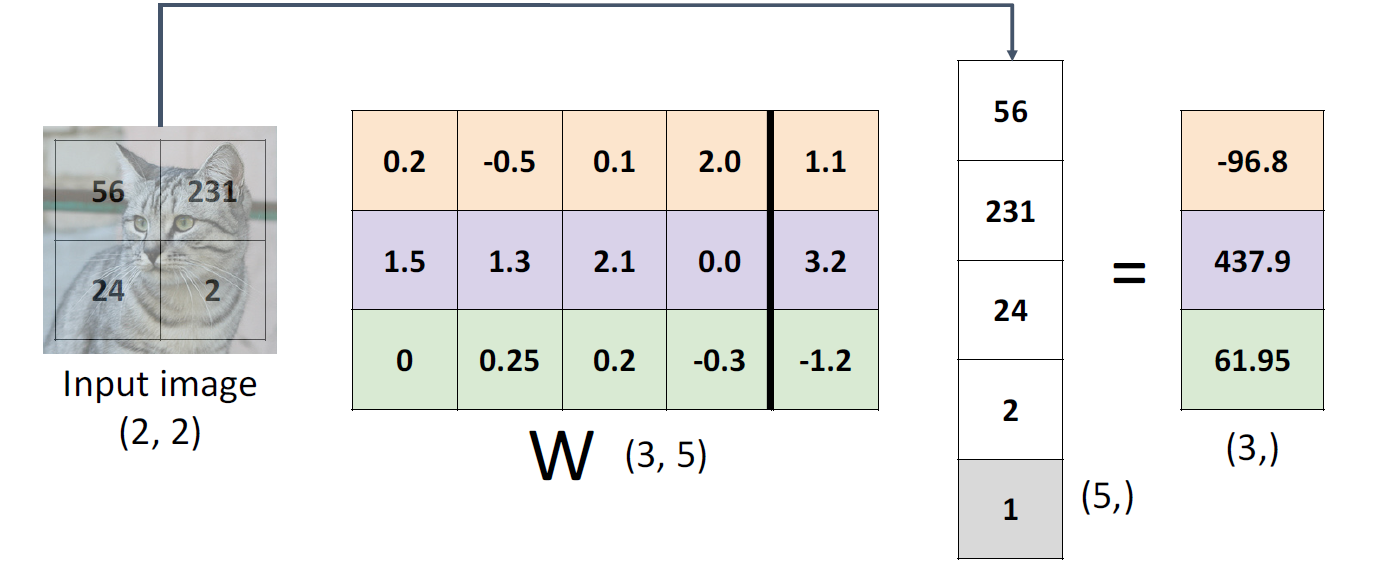
线性分类的效果
线性分类是在一个多维空间里面用多个超平面进行分割
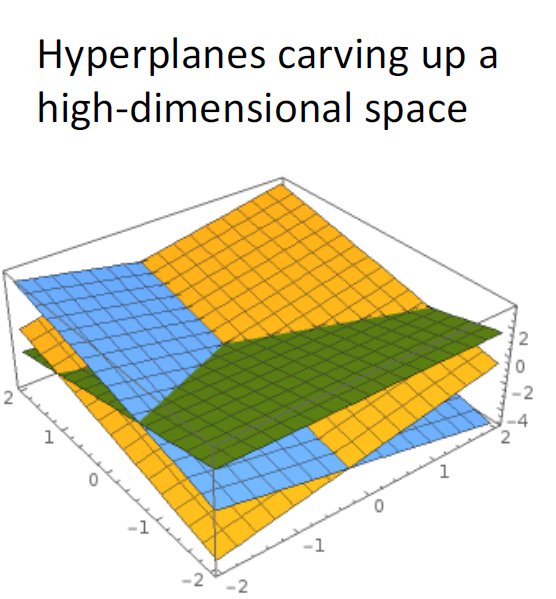
线性分类的缺点
很多问题不能通过线性分类来解决,比如在上个世纪把人工智能打入谷底的XOR问题
Loss函数" class="reference-link">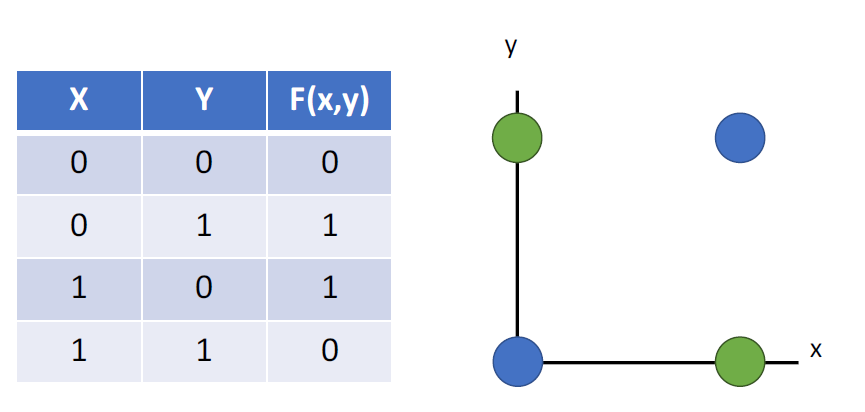 Loss函数
Loss函数
如何选一个好的W让分类器表现有优秀
- 找一个好的loss函数
- 找一个能让loss函数值最小的W
高的Loss:分类器表现糟糕
低的Loss:分类器表现优秀
对于一个数据集, x i x_i xi是图片, y i y_i yi是标签
{ ( x i ) , y i } i = 1 N \{(x_i), y_i\}^N_{i=1} { (xi),yi}i=1N
那么Loss函数就是用于描述预测值与实际值中差异的函数
L i ( f ( x i , W ) , y i ) L_i(f(x_i, W), y_i) Li(f(xi,W),yi)
通常会用一个数据集的平均Loss来表示这个分类器在这个数据集上的表现
L = 1 N ∑ i L i ( f ( x i , W ) , y i ) L={1\over N}\sum_i L_i(f(x_i, W), y_i) L=N1i∑Li(f(xi,W),yi)
Multiclass SVM Loss
L i = ∑ j ≠ y i ( 0 , s j − s y i + 1 ) L_i=\sum_{j\neq y_i}(0, s_j-s_{y_i}+1) Li=j=yi∑(0,sj−syi+1)
对于这张猫图,它对于这几个分类计算出来的结果是这样的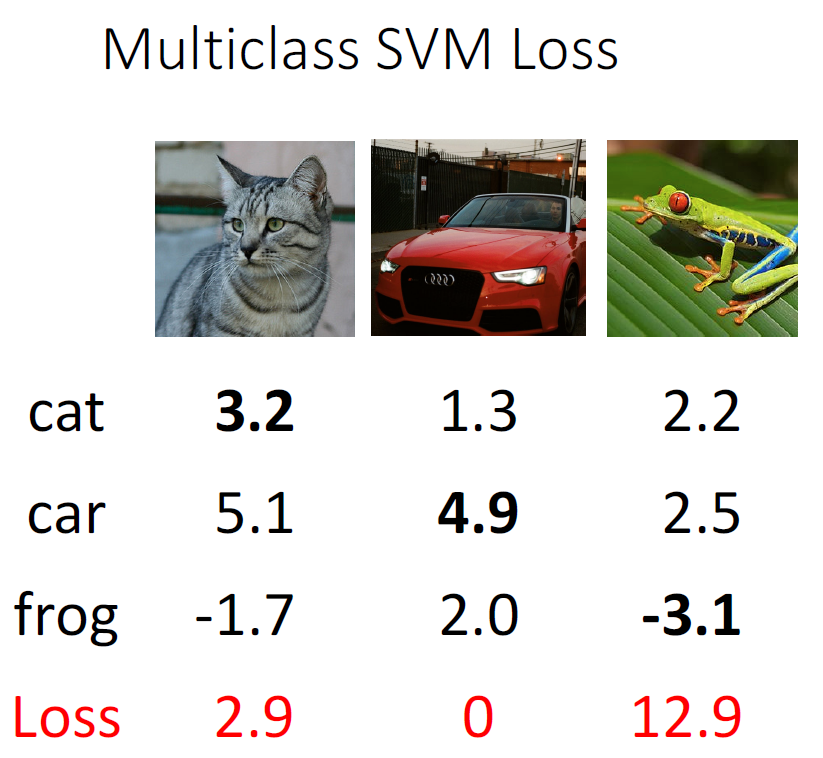
那么它的SVM Loss就是
L 0 = m a x ( 0 , 5.1 − 3.2 + 1 ) + m a x ( 0 , − 1.7 − 3.2 + 1 ) = m a x ( 0 , 2.9 ) + m a x ( 0 , − 3.9 ) = 2.9 \begin{aligned} L_0 &= max(0, 5.1-3.2+1) + max(0, -1.7-3.2+1) \\ & = max(0, 2.9) + max(0, -3.9)\\ & = 2.9 \end{aligned} L0=max(0,5.1−3.2+1)+max(0,−1.7−3.2+1)=max(0,2.9)+max(0,−3.9)=2.9
平均的Loss则是 L = ( 2.9 + = + 12.9 ) / 3 = 5.27 L = (2.9+=+12.9)/3=5.27 L=(2.9+=+12.9)/3=5.27
正则化
正则化的目的是为了防止分类器在训练集上表现过好,防止过拟合现象;同时可以增加曲率从而优化训练的过程
L ( W ) = 1 N ∑ i = 1 N L i ( f ( x i , W ) , y i ) + λ R ( W ) L(W) = {1\over N}\sum_{i=1}^NL_i(f(x_i, W), y_i)+\lambda R(W) L(W)=N1i=1∑NLi(f(xi,W),yi)+λR(W)
常用的正则化方式
- L2正则: R ( W ) = ∑ k ∑ l W k , l 2 R(W)=\sum_k\sum_lW^2_{k,l} R(W)=∑k∑lWk,l2
- L1正则: R ( W ) = ∑ k ∑ l ∣ W k , l ∣ R(W)=\sum_k\sum_l \mid W_{k,l}\mid R(W)=∑k∑l∣Wk,l∣
- Elastic Net(L1+L2): R ( W ) = ∑ k ∑ l β W k , l 2 + ∣ W k , l ∣ R(W)=\sum_k\sum_l \beta W^2_{k,l} + \mid W_{k,l}\mid R(W)=∑k∑lβWk,l2+∣Wk,l∣
- Dropout:丢掉一些训练结果
- 归一化
- Cutout,Mixup, Stochastic depth
正则化的效果

对于w1和w2,他们的训练结果都是一样的,但是对于L2正则函数而言,他们会更喜欢均匀分布的权重,即w2。
Cross-Entropy Loss
通过将分数改变为概率,即,对于 X i X_i Xi是 y = k y = k y=k的概率是:
P ( Y = k ∣ X = x i ) = e s k ∑ j e s j P(Y=k\mid X=x_i)={e^{s_k}\over \sum_je^{s_j}} P(Y=k∣X=xi)=∑jesjesk
那么它的Loss函数就是
L i = − l o g P ( Y = y j ∣ X = x i ) L_i=-logP(Y=y_j\mid X=x_i) Li=−logP(Y=yj∣X=xi)
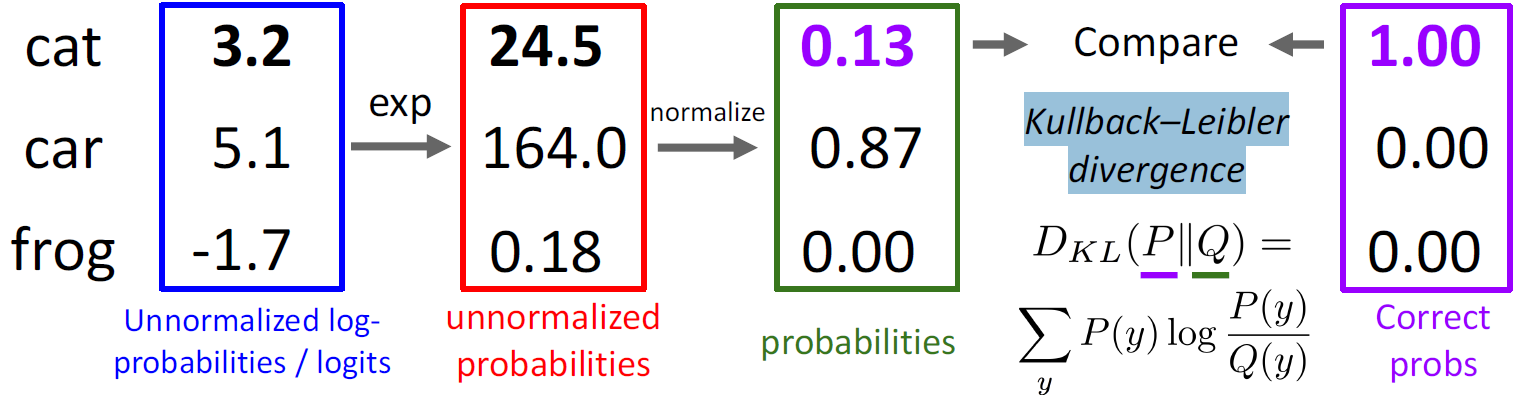
利用KL散度衡量两个分布之间的差异。





























还没有评论,来说两句吧...