计算机视觉与深度学习系列博客传送门
【计算机视觉与深度学习】线性分类器（一）

损失函数再探讨

让我们回到损失函数的一般定义 L = 1 N ∑ i L i ( f ( x i , W ) , y i ) L=\frac{1}{N}\sum_iL_i(f(\bm x_i,\bm W),y_i) L=N1i∑Li(f(xi,W),yi)那么，若存在一个 W \bm W W使得损失 L = 0 L=0 L=0，那么这个 W \bm W W是否唯一？
假设两个线性分类器 f 1 ( x , W 1 ) = W 1 x , f 2 ( x , W 2 ) = W 2 x \bm f_1(\bm x,\bm W_1)=\bm W_1 \bm x,\bm f_2(\bm x,\bm W_2)=\bm W_2 \bm x f1(x,W1)=W1x,f2(x,W2)=W2x，其中 W 2 = 2 W 1 \bm W_2=2 \bm W_1 W2=2W1，对于一个样本（假设此样本的标签为car），已知分类器1的打分结果如下表所示：

标签	bird	cat	car
得分	3.1	-2.6	4.3

根据多类支持向量机损失的定义 L i = ∑ j ≠ y i max ⁡ ( 0 , s i j − s y i + 1 ) L_i=\sum_{j\neq y_i}\max(0,s_{ij}-s_{y_i}+1) Li=j=yi∑max(0,sij−syi+1)不难计算出分类器1的损失值为0。
由 W 2 = 2 W 1 \bm W_2=2 \bm W_1 W2=2W1很容易计算出分类器2的打分结果：

标签	bird	cat	car
得分	6.2	-5.2	8.6

同样地，根据多类支持向量机损失的定义，我们可以计算出分类器2的损失值也为0。
这样一来，我们就可以回答上面提出的问题了：若存在一个 W \bm W W使得损失 L = 0 L=0 L=0，这个 W \bm W W并不是唯一的。那么，既然这两个分类器都具有相同的损失值0，应当选择这两个分类器中的哪一个呢？

正则项

为了解决上面提出的问题，此处引入正则项的概念。将损失函数稍作修改 L = 1 N ∑ i L i ( f ( x i , W ) , y i ) + λ R ( W ) L=\frac{1}{N}\sum_iL_i(f(\bm x_i,\bm W),y_i)+\lambda R(\bm W) L=N1i∑Li(f(xi,W),yi)+λR(W)其中， 1 N ∑ i L i ( f ( x i , W ) , y i ) \frac{1}{N}\sum_iL_i(f(\bm x_i,\bm W),y_i) N1∑iLi(f(xi,W),yi)叫做数据损失，衡量的是模型的预测结果与训练集的真实标签之间的匹配程度； λ R ( W ) \lambda R(\bm W) λR(W)叫做正则损失， R ( W ) R(\bm W) R(W)是一个与权值有关、与训练集数据无关的函数， λ \lambda λ是一个控制正则损失在总损失中所占的比重的超参数。引入正则损失可以避免模型在训练集上学习得“太好”，即正则项可以在一定程度上避免过拟合问题，提高模型的泛化性能。
接下来我们对超参数 λ \lambda λ进行讨论。超参数指的是在开始学习过程之前设置值的参数，它并不能通过学习得到，例如神经网络训练的batch size、epochs、learning rate等也都是超参数。超参数一般都会对模型性能有着重要的影响。对于上面的损失函数，当 λ = 0 \lambda=0 λ=0时，优化结果仅与数据损失有关；当 λ = ∞ \lambda=\infty λ=∞时，优化结果与数据损失无关，仅考虑权重损失，此时系统最优解为 W = 0 \bm W=\bm 0 W=0。
我们常用的正则项之一是L2正则项。L2正则项的定义为 R ( W ) = ∑ k ∑ l W k , l 2 R(\bm W)=\sum_k \sum_l \bm W^2_{k,l} R(W)=k∑l∑Wk,l2假设有一组样本 x = [ 1 1 1 1 ] \bm x=\begin{gathered}\begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}\end{gathered} x=⎣⎢⎢⎡1111⎦⎥⎥⎤分类器1 W 1 T = [ 1 0 0 0 ] \bm W_1^T=\begin{gathered}\begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix}\end{gathered} W1T=[1000]分类器2 W 2 T = [ 0.25 0.25 0.25 0.25 ] \bm W_2^T=\begin{gathered}\begin{bmatrix} 0.25 & 0.25 & 0.25 & 0.25 \end{bmatrix}\end{gathered} W2T=[0.250.250.250.25]分类器输出 W 1 x = W 2 x = 1 \bm W_1 \bm x=\bm W_2 \bm x=1 W1x=W2x=1由损失函数定义易得两个分类器的数据损失是相等的。为了比较这两个分类器，我们可以计算它们的正则损失。由定义可得 R ( W 1 ) = 1 2 + 0 2 + 0 2 + 0 2 = 1 R(\bm W_1)=1^2+0^2+0^2+0^2=1 R(W1)=12+02+02+02=1 R ( W 2 ) = 0.2 5 2 + 0.2 5 2 + 0.2 5 2 + 0.2 5 2 = 0.25 R(\bm W_2)=0.25^2+0.25^2+0.25^2+0.25^2=0.25 R(W2)=0.252+0.252+0.252+0.252=0.25分类器2的正则损失更小一些，即分类器1的总损失大于分类器2，因此我们选择分类器2。
L2正则化对大数值权值进行惩罚，分散权值，鼓励分类器将所有维度的特征利用起来，而非强烈地依赖其中少数几维特征。正则项让模型有了偏好。
除了L2正则项之外，常用的正则化方法还有L1正则项 R ( W ) = ∑ k ∑ l ∣ W k , l ∣ R(\bm W)=\sum_k \sum_l |\bm W_{k,l}| R(W)=k∑l∑∣Wk,l∣和弹性网络 (Elastic net) 正则项 R ( W ) = ∑ k ∑ l α ∣ W k , l ∣ + β W k , l R(\bm W)=\sum_k \sum_l \alpha|W_{k,l}|+\beta \bm W_{k,l} R(W)=k∑l∑α∣Wk,l∣+βWk,l

参数优化

对于模型来说，由于损失函数 L L L是一个与参数 W \bm W W有关的函数，所以参数优化的目标就是找到使损失函数 L L L达到最优的那组参数 W \bm W W。最直接的方法就是使 ∂ L ∂ W = 0 \frac{\partial L}{\partial \bm W}=0 ∂W∂L=0但通常 L L L的形式比较复杂，很难通过上式直接求出 W \bm W W。另一种求解方法是使用梯度下降算法迭代更新 W \bm W W。梯度下降法是一个广泛被用来最小化模型误差的参数优化算法。梯度下降法通过多次迭代，并在每一步中最小化成本函数来估计模型的参数。梯度下降的算法流程为：

while True:
权值的梯度 ← 计算梯度(损失, 训练样本, 权值)
权值 ← 权值 - 学习率 × 权值的梯度

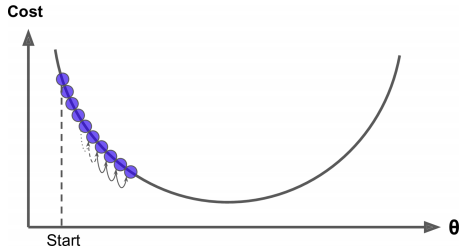
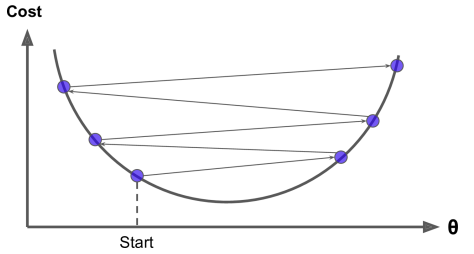
假设我们在一座山上，快速到达山脚的一个策略就是沿着最陡的方向下坡。梯度下降中的一个重要参数是每一步的步长，这取决于超参数学习率 (learning rate)。如果学习率太低，算法需要经过大量的迭代才能收敛，这将会耗费大量的时间。反过来说，如果学习率太高，会导致算法发散。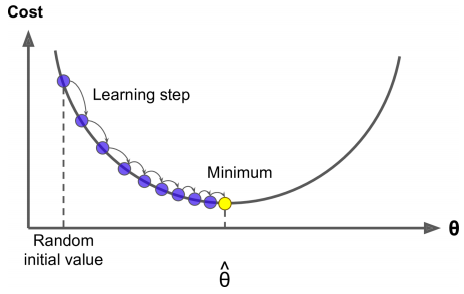
在这里插入图片描述

计算梯度有两种方法。第一种方法是数值法 d L ( w ) d w = lim ⁡ h → 0 L ( w + h ) − L ( w ) h \frac {\mathrm{d}L(w)}{\mathrm{d}w}=\lim_{h→0} \frac{L(w+h)-L(w)}{h} dwdL(w)=h→0limhL(w+h)−L(w)其中 h h h是一个很小的数。例如，计算函数 L ( w ) = w 2 L(w)=w^2 L(w)=w2在 w = 1 w=1 w=1处的梯度 d L ( w ) d w = lim ⁡ h → 0 L ( w + h ) − L ( w ) h ≈ L ( 1 + 0.0001 ) − L ( 1 ) 0.0001 = 2.0001 \frac {\mathrm{d}L(w)}{\mathrm{d}w}=\lim_{h→0} \frac{L(w+h)-L(w)}{h}≈\frac{L(1+0.0001)-L(1)}{0.0001}=2.0001 dwdL(w)=h→0limhL(w+h)−L(w)≈0.0001L(1+0.0001)−L(1)=2.0001但是，使用数值法计算梯度计算量大且不精确。我们还可以使用第二种方法——解析法来计算梯度。
还以计算函数 L ( w ) = w 2 L(w)=w^2 L(w)=w2在 w = 1 w=1 w=1处的梯度为例 ▽ L ( w ) = 2 w \triangledown L(w)=2w ▽L(w)=2w ▽ w = 1 L ( w ) = 2 \triangledown _{w=1}L(w)=2 ▽w=1L(w)=2解析法的特点是精确且速度快，但是导函数的推导容易出错。
在真实应用中，我们通常使用解析法来计算梯度，但这并不意味着数值法没有用武之地。数值法计算梯度一般用于解析法计算梯度的正确性校验。
对于引入正则项的损失函数 L ( W ) = 1 N ∑ i = 1 N L i ( x i , y i , W ) + λ R ( W ) L(\bm W)=\frac{1}{N}\sum_{i=1}^{N}L_i(\bm x_i,y_i,\bm W)+\lambda R(\bm W) L(W)=N1i=1∑NLi(xi,yi,W)+λR(W)计算其梯度为 ▽ W L ( W ) = 1 N ∑ i = 1 N ▽ W L i ( x i , y i , W ) + λ ▽ W R ( W ) \triangledown _{\bm W}L(\bm W)=\frac{1}{N}\sum_{i=1}^{N}\triangledown_{\bm W}L_i(\bm x_i,y_i,\bm W)+\lambda \triangledown_{\bm W}R(\bm W) ▽WL(W)=N1i=1∑N▽WLi(xi,yi,W)+λ▽WR(W)
梯度下降算法虽然很准确，但是当 N N N很大时，权值的梯度的计算量很大。随机梯度下降算法是一个与之相反的极端。随机梯度下降算法每一次在训练集中随机选择一个样本，并且仅基于该样本来计算梯度，即：

while True:
数据 ← 从训练数据采样(训练数据, 1)
权值的梯度 ← 计算梯度(损失, 数据, 权值)
权值 ← 权值 - 学习率 × 权值的梯度

这样让算法的迭代速度快了很多，但是由于算法的随机性质，单个样本的训练可能会带来很多噪声，并不是每一次迭代都向着整体最优化方向，而是不断地上上下下，但从整体来看还是在慢慢下降，最终会非常接近最小值。但即使它到达了最小值，依旧还会持续反弹，永远不会停止。随机梯度下降算法停下来的参数值肯定是足够好的，但并不是最优的。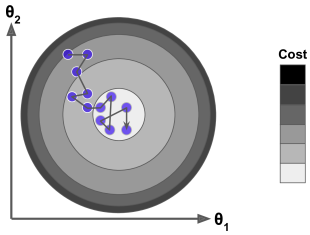
在这里插入图片描述
小批量梯度下降算法是另一种梯度下降算法。在每一步中，不同于批量梯度下降（基于完整的训练集）和随机梯度下降（仅基于某一个样本），小批量梯度下降每次随机选择 m m m个样本组成小型批量数据集，计算损失并更新梯度，即：