二叉树之已知前序遍历、中序遍历求二叉树-蒲公英云

二叉树之已知前序遍历、中序遍历求二叉树

以上一篇的二叉树为例https://blog.csdn.net/u012093557/article/details/106496635
在这里插入图片描述
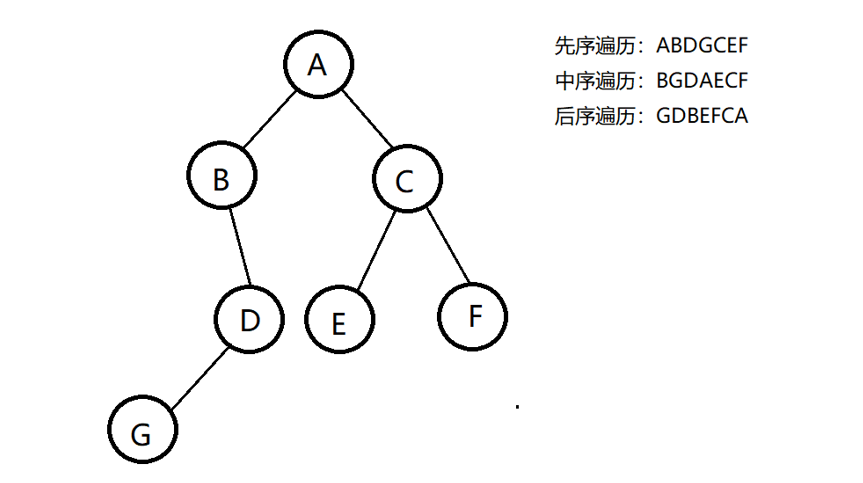
这个二叉树的前序、中序分别如下所示，
1, 2,3,4,5,6,7,8, 9,10,11,
4,3,2,6,5,8,7, 1, 10,9,11,

解题思路：前序遍历是根-》左-》右，那么第一个数一定是根节点，这里1就是根节点。中序遍历左-》根-》右，那么1拿到中序遍历就可以分割左、右子树，中序遍历左子树：4,3,2,6,5,8,7,右子树：10,9,11,。且可按照长度，在前序遍历结果中，可找到左子树前序遍历2,3,4,5,6,7,8,，右子树9,10,11,。分割子树完毕，子树是否可以再按照以上分析继续解析，此时如果可以，那么就形成了递归。接下来看一下代码实现

TwoTree* calATree(vector<int> preorderList,vector<int> middleOrderList)
{
    // 前序的首位是根，根再分割中序可以找到左子树，右子树
    if ((preorderList.size() != middleOrderList.size()) || preorderList.empty())
    {
        return NULL;
    }
    // 创建根节点
    int value = preorderList.front();
    TwoTree* node = new TwoTree(preorderList.front());
    // 查找 前序根结点在中序中的位置
    uint nodeIndex = -1;
    for (nodeIndex = 0; nodeIndex < middleOrderList.size(); nodeIndex++ )
    {
        if (middleOrderList.at(nodeIndex) == value)
        {
            break;
        }
    }
    // 根据前序根结点在中序中的位置分割左子树、右子树
    node->left =(nodeIndex == 0)? NULL:calATree(vector<int> (preorderList.begin() + 1, preorderList.begin() + nodeIndex + 1)
                          ,vector<int> (middleOrderList.begin(), middleOrderList.begin() + nodeIndex));
    node->right = (nodeIndex + 1 == middleOrderList.size()) ? NULL:calATree(vector<int> (preorderList.begin() + 1 + nodeIndex, preorderList.end())
                          ,vector<int> (middleOrderList.begin() + nodeIndex+1, middleOrderList.end()));
    return node;
}