LLE降维-蒲公英云

LLE降维

LLE 是 Locally Linear embedding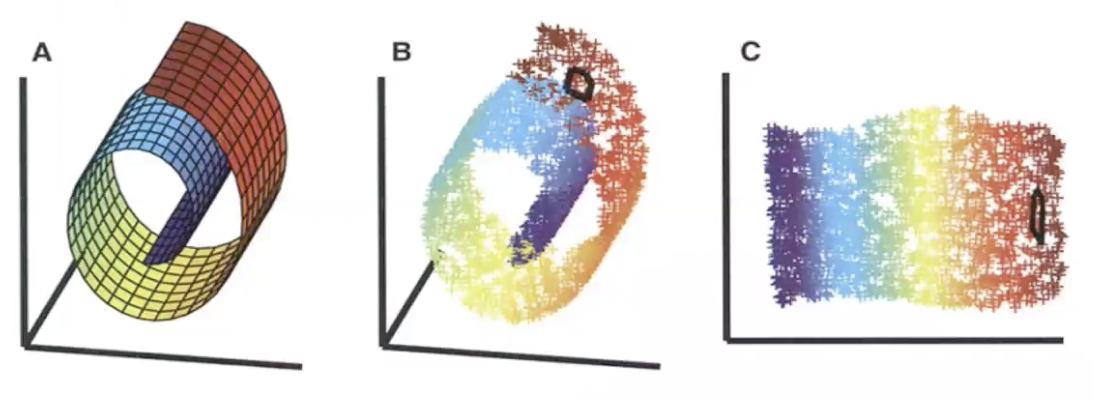
在这里插入图片描述
直观是在样本点的高维空间相邻近的话，可以用低维的子空间描述。

基本原理分三步：
（1）找到邻居 neighbors .(可以使用多种方法，邻居K的数目选择影响很大)
（2）使用周围的邻居作为基向量， reconstruct with linear weights
minimize reconstruction error.

m i n W ε ( W ) = ∑ i ∣ ∣ x i − ∑ j ∈ N i W i j x j ∣ ∣ 2 2 \underset{W}{min}\varepsilon (W) = \sum_i||x_i - \sum_{j\in N_i}W_{ij}x_j||^2_2 Wminε(W)=∑i∣∣xi−∑j∈NiWijxj∣∣22,

∑ i ∣ ∣ x i − ∑ j ∈ N i W i j x j ∣ ∣ 2 2 = ∑ j ∣ ∣ W i j ( x i − x j ) ∣ ∣ 2 2 = ∑ j k W i j W i k G j k = W i T G W i \sum_i||x_i - \sum_{j\in N_i}W_{ij}x_j||^2_2=\sum_j||W_{ij}(x_i-x_j)||^2_2=\sum_{jk}W_{ij}W_{ik}G_{jk}=W_i^TGW_i ∑i∣∣xi−∑j∈NiWijxj∣∣22=∑j∣∣Wij(xi−xj)∣∣22=∑jkWijWikGjk=WiTGWi,

G j k = ( x i − x j ) T ( x i − x k ) , ∀ j , k ∈ N i G_{jk}=(x_i-x_j)^T(x_i-x_k), \forall j,k \in N_i Gjk=(xi−xj)T(xi−xk),∀j,k∈Ni
使用拉格朗日方法：

2 G W i − λ I = 0 , ∑ j W i j = 1 2GW_i-\lambda I=0, \sum_jW_{ij}=1 2GWi−λI=0,∑jWij=1

W i = G − 1 I I T G − 1 I W_i = \frac{G^{-1}I}{I^TG^{-1}I} Wi=ITG−1IG−1I

s . t . ∑ j W i j = 1 , ∀ i s.t. \sum_jW_{ij}=1 , \forall _i s.t.∑jWij=1,∀i

为了防止G病态多个解，加入二范数
m i n W i W i T G W i + γ W i T W i min_{W_i}W_i^TGW_i + \gamma W_i^TW_i minWiWiTGWi+γWiTWi
得到
2 ( G + γ I ) W i − λ I = 0 2(G+\gamma I)W_i - \lambda I=0 2(G+γI)Wi−λI=0

W i = ( G + γ I ) − 1 I I T ( G + γ I ) − 1 I W_i = \frac{(G+\gamma I)^{-1}I}{I^T(G+\gamma I)^{-1}I} Wi=IT(G+γI)−1I(G+γI)−1I

(3) Map to embedding coordinates
m i n Y ϕ ( Y ) = ∑ i ∣ ∣ y i − ∑ j ∈ N i W i j y i ∣ ∣ 2 2 \underset{Y}{min}\phi(Y) = \sum_i||y_i-\sum_{j \in N_i}W_{ij}y_i||^2_2 Yminϕ(Y)=∑i∣∣yi−∑j∈NiWijyi∣∣22

对y要做约束，不然有很多解，比如平移。

s . t . ∑ i y i = 0 , 1 N ∑ i y i y i T = I s.t. \sum_iy_i=0, \frac{1}{N}\sum_iy_iy_i^T=I s.t.∑iyi=0,N1∑iyiyiT=I

解决方法拉格朗日方法， eigenvalue problem
F = 1 2 ∑ i ∣ ∣ y i − ∑ j W i j y j ∣ ∣ 2 2 − 1 2 ∑ α β λ α β ( 1 N ∑ i y i α y i β − δ α β ) F=\frac{1}{2}\sum_i||y_i-\sum_jW_{ij}y_j||^2_2-\frac{1}{2}\sum_{\alpha \beta}\lambda_{\alpha \beta}(\frac{1}{N}\sum_iy_i\alpha y_i \beta - \delta\alpha \beta) F=21∑i∣∣yi−∑jWijyj∣∣22−21∑αβλαβ(N1∑iyiαyiβ−δαβ)

( 1 − W ) T ( 1 − W ) Y = 1 N Y Λ , w h e r e Λ α β = λ α β (1-W)^T(1-W)Y = \frac{1}{N}Y\Lambda, where \Lambda_{\alpha \beta} = \lambda _{\alpha \beta} (1−W)T(1−W)Y=N1YΛ,whereΛαβ=λαβ