m数据结构 day11 树（四）把普通树和森林转换为二叉树（神操作），普通树和森林的遍历转化为二叉树的遍历

r囧r小猫 2023-03-13 02:49 129阅读 0赞

文章目录

  • 借助孩子兄弟表示法把树，森林转换为二叉树
    • 把普通树转换为二叉树
      • 二叉树变回普通树
    • 森林转换为二叉树
      • 把由森林转换到的二叉树逆转换为森林
  • 普通树和森林的遍历
    • 普通树的遍历
      • 先根遍历：和它转换为的二叉树的前序遍历一样
      • 后根遍历：和它转换为的二叉树的中序遍历一样
    • 森林的遍历
      • 前序遍历：依次对每棵树先根遍历；和它转换为的二叉树的前序遍历一样
      • 后序遍历：依次对每棵树后根遍历；和它转换为的二叉树的中序遍历一样

借助孩子兄弟表示法把树，森林转换为二叉树

树的孩子兄弟表示法可以把任何树存储为一个二叉链表，即每个结点只有两个指针域，因此最多只指向两个结点。

我们也可以利用孩子兄弟表示法把任何普通树，甚至普通森林转换为一颗二叉树！这会见识到了孩子兄弟表示法的牛逼了，，，兄弟们齐心办事果然了不得。

为什么说树和森林转换为二叉树的过程中，用到了孩子兄弟表示法呢？
因为你很快能看到，下面的转换中，每个结点只保留自己的第一个孩子成为左孩子，而其他所有孩子，即第一个孩子的兄弟们，被横着连在第一个孩子右边，然后不断成为自己左边兄弟的右孩子。

把普通树转换为二叉树

我去，一波晃眼操作，普通树就真的变身二叉树了。。。牛逼。

分为三步：
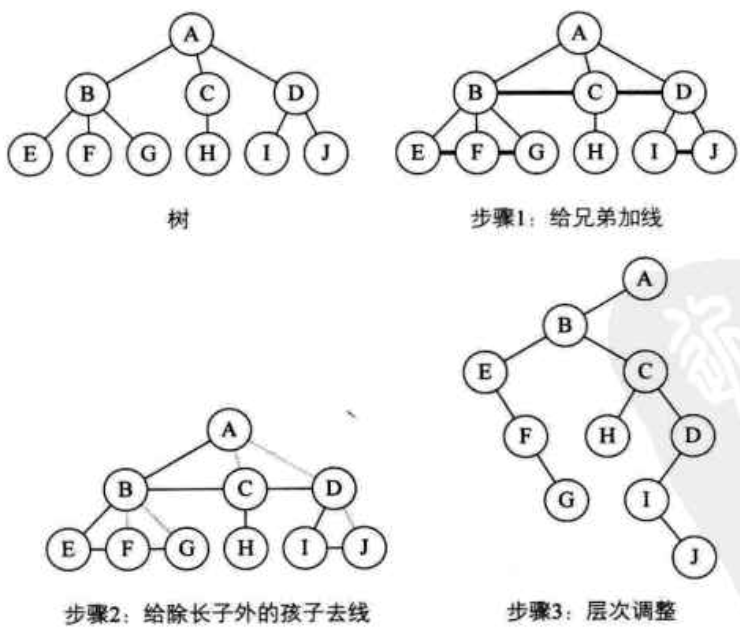
在这里插入图片描述

在这里插入图片描述

二叉树变回普通树

这个二叉树要想返回去得到原树，反着操作就行：
在这里插入图片描述

上半部分完成了第2,3两步的反操作，双线是添回的长子之外的线

下半部分去除了兄弟之间的连线，得到了原树

森林转换为二叉树

牛逼牛逼，没有做不到，只有想不到

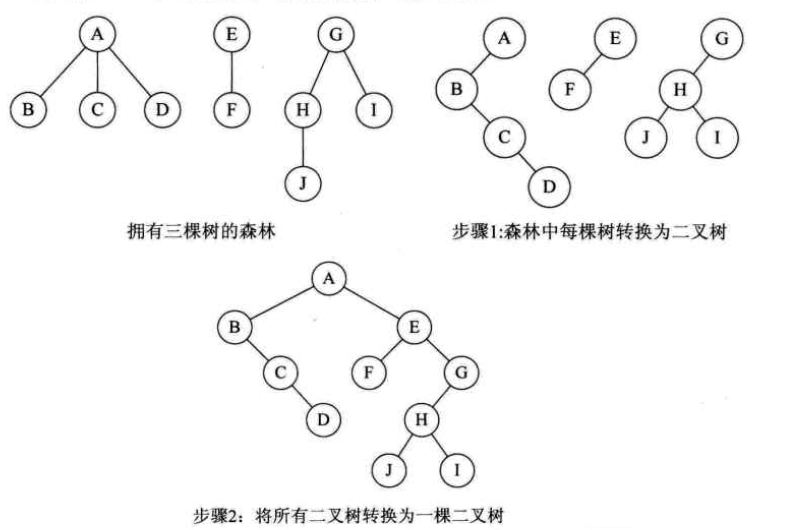
在这里插入图片描述在这里插入图片描述

把由森林转换到的二叉树逆转换为森林

由普通树转换得到的二叉树的根结点一定没有右孩子；

根结点有右孩子则一定是由森林转换来的，但是这句必须要按照下面的顺序（从根节点开始逐渐分离右子树）来判断，不能看着H有右孩子就也认为H是森林转换来的。

这是把由森林转换到的二叉树逆转回去的基本原理。

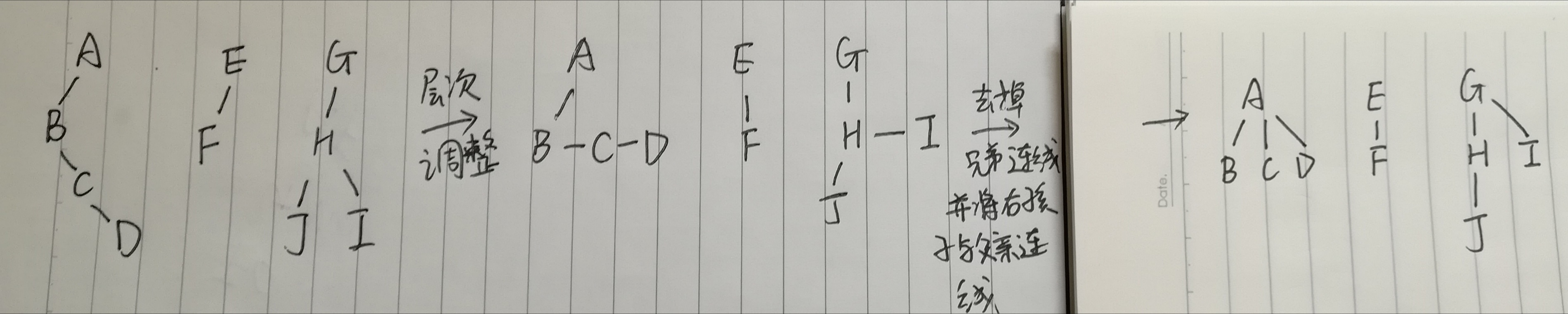
在这里插入图片描述
在这里插入图片描述

普通树和森林的遍历

注意之前学习的前序，中序，后序，层次遍历都是针对二叉树的遍历。不是对于普通树的。而这里说的先根遍历和后根遍历则是完全针对普通树，森林的前序和后序遍历也是针对普通森林的。

但是学完了普通树的遍历和森林的遍历以后，你会发现，普通树和森林的遍历都可以转换为二叉树的遍历：

  • 普通树的先根遍历和其转换为的二叉树的前序遍历结果相同。
  • 普通树的后根遍历和其转换为的二叉树的中序遍历结果相同。
  • 森林的前序遍历和其转换为的二叉树的前序遍历结果相同。
  • 森林的后序遍历和其转换为的二叉树的中序遍历结果相同。

普通树的遍历

先根遍历：和它转换为的二叉树的前序遍历一样

先访问根结点，然后依次先根遍历每一棵子树。也用递归。

例子：

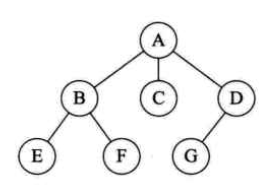
在这里插入图片描述
先根遍历结果：ABEFCDG

上图树转化为的二叉树是：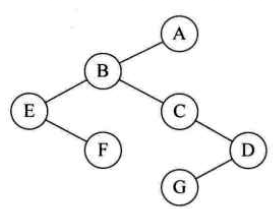
在这里插入图片描述

他的前序遍历结果是：ABEFCDG

所以普通树的先根遍历和它转换为的二叉树的前序遍历结果一样。

后根遍历：和它转换为的二叉树的中序遍历一样

先依次后根遍历每一棵子树，再访问根结点。
后根遍历结果：EFBCGDA
转换为的二叉树的中序遍历序列：EFBCGDA

所以普通树的后根遍历和它转换为的二叉树的中序遍历结果一样。并不和二叉树的后序遍历一样哦。

转换为的二叉树的后序遍历序列：FEGDCBA

森林的遍历

前序遍历：依次对每棵树先根遍历；和它转换为的二叉树的前序遍历一样

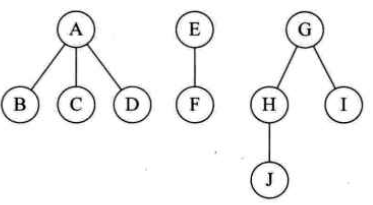
在这里插入图片描述

例子：
在这里插入图片描述

ABCDEFGHJI

后序遍历：依次对每棵树后根遍历；和它转换为的二叉树的中序遍历一样

在这里插入图片描述

BCDAFEJHIG

上图的森林转换得到的二叉树是：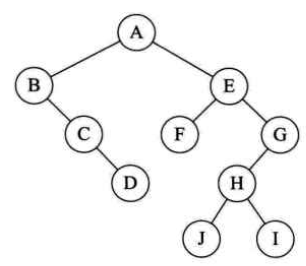
在这里插入图片描述

如果对这个二叉树前序遍历，则顺序为ABCDEFGHJI，和森林的前序遍历的结果相同。

如果对这个二叉树进行后序遍历，则顺序为DCBFJIHGEA，和森林的后序遍历的结果不相同。

如果对这个二叉树进行中序遍历，则顺序为BCDAFEJHIG,和森林的后序遍历的结果相同。

所以，森林转换得到的二叉树的中序遍历和森林的后序遍历结果相同。
森林转换得到的二叉树的前序和森林的前序相同。

发表评论

表情：
评论列表 （有 0 条评论，129人围观）

还没有评论，来说两句吧...

相关阅读

    相关 树 森林 二叉树 遍历

    所谓遍历(Traversal)，是指沿着某条搜索路线，依次对树（或图）中每个节点均做一次访问。 访问结点所做的操作依赖于具体的应用问题， 具体的访问操作可能是检查节点的值、

    悠悠悠悠/ 0 赞/ 118 阅读