【神经网络和深度学习】—— 从理论到实践深入理解RNN（Recurrent Neural Network） 基于Pytorch实现

淩亂°似流年 2023-07-22 09:21 9阅读 0赞

文章目录

  • 一、RNN的理论部分
    • 1.1 Why Recurrent Neural Network
    • 1.2 RNN 的工作原理解析
      • 1.2.1 数据的定义部分
      • 1.2.2 RNN 的具体运算过程
    • 1.2.3 几种不同类型的 RNN
  • 二、基于Pytorch的RNN实践部分
    • 2.1 在Pytorch里面对 RNN 输入参数的认识
    • 2.2 nn.RNN 里面的 forward 方法：
    • Example：利用RNN进时间序列的预测

一、RNN的理论部分

1.1 Why Recurrent Neural Network

我们之前学习的 DNN，CNN。在某一些领域都取得了显著的成效（例如 CNN 在 CV 领域的卓越成绩）。但是他们都只能单独的取处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。

但是，当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列； 当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。

所以为了解决一些这样类似的问题，能够更好的处理序列的信息，RNN就诞生了

1.2 RNN 的工作原理解析

1.2.1 数据的定义部分

首先，我们约定一个数学符号：我们用 x x x 表示输入的时间序列。举一个最常见的例子：如果我们需要进行文本人名的识别。我们将会给 RNN 输入这样一个时间序列 x x x： H a r r y P o t t e r a n d H e r m i o n e G r a n g e r i n v e n t e d a n e w s p e l l Harry\space\space Potter\space\space and\space\space Hermione\space\space Granger\space\space invented\space\space a\space\space new\space\space spell HarryPotterandHermioneGrangerinventedanewspell
我们定义 x < t > x^{} x 作为 t t t 时刻序列对应位置的输入。 T x Tx Tx 表示序列的长度。也就是说，我们现在是把这一句完整的话拆分成了 T x Tx Tx 个单词。其中每一个单词用 x < t > x^{} x 表示。例如这里的 H a r r y Harry Harry 就表示成 x < 1 > x^{<1>} x<1>、 G r a n g e r Granger Granger 就表示成 x < 5 > x^{<5>} x<5>。因此，现在整个句子就可以表示成： [ x < 1 > x < 2 > x < 3 > x < 4 > x < 5 > x < 6 > x < 7 > x < 8 > x < 9 > ] \begin{bmatrix} x^{<1>} & x^{<2>} & x^{<3>} & x^{<4>} & x^{<5>}& x^{<6>}& x^{<7>} & x^{<8>} & x^{<9>} \end{bmatrix} [x<1>x<2>x<3>x<4>x<5>x<6>x<7>x<8>x<9>]

下一步：因为我们的任务是找出这一句话里面是人名的部分，而我们知道，每一个词都有可能是人名，所以现在看起来，我们的 RNN 的输出应该要和这个句子的长度保持一致。我们用 y < t > y^{} y 来表示 RNN 在 t t t 时刻的输出。所以，RNN 的输出可以表示成： [ y < 1 > y < 2 > y < 3 > y < 4 > y < 5 > y < 6 > y < 7 > y < 8 > y < 9 > ] \begin{bmatrix} y^{<1>} & y^{<2>} & y^{<3>} & y^{<4>} & y^{<5>} & y^{<6>} & y^{<7>} & y^{<8>} & y^{<9>} \end{bmatrix} [y<1>y<2>y<3>y<4>y<5>y<6>y<7>y<8>y<9>]

用 T y Ty Ty 表示输出的长度，在这里 T x = T y Tx = Ty Tx=Ty。但是当然 ，他么两个可以不相等，这将在后面介绍。

我们用 0 表示不是人名，1 表示是人名。所以上面这个句子对应的标签 l a b e l label label 应该是： [ 1 1 0 0 1 1 0 0 0 0 ] \begin{bmatrix} 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \end{bmatrix} [1100110000]

下面，我们应该如何表示 x < t > x^{} x 呢？首先能够想到的一种方法是建立一个 V o c a b u l a r y Vocabulary Vocabulary 库，这个库尽可能包含大部分的词。例如像下面这样： [ a a b a c k ⋮ h a r r y ⋮ p o t t e r ⋮ z u l u ] \begin{bmatrix} a\\ aback\\ \vdots\\ harry\\ \vdots\\ potter\\ \vdots\\ zulu \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡aaback⋮harry⋮potter⋮zulu⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
假设这个 V o c a b u l a r y Vocabulary Vocabulary 库 是一个 10000x1 的向量。

然后我们对准备作为输入的这句话： H a r r y P o t t e r a n d H e r m i o n e G r a n g e r i n v e n t e d a n e w s p e l l Harry\space\space Potter\space\space and\space\space Hermione\space\space Granger\space\space invented\space\space a\space\space new\space\space spell HarryPotterandHermioneGrangerinventedanewspell
的每一个单词 x < t > x^{} x 都可以表示成这个 10000 x 1 的向量，其中 x < t > x^{} x 和 词汇库里面相等的那个位置记为 1 ，不相等的地方记为 0。也就是构成一个 o n e − h o t one-hot one−hot 编码。这个 10000 ，将会是我们后面将要提到的 i n p u t _ s i z e input\_size input_size

那么，这个是一个样本的情况。如果存在多个样本（也就是采用 m i n i _ b a t c h mini\_batch mini_batch 的方法，那么我们定义 X ( i ) < t > X(i)^{} X(i)表示为第 i i i 个样本在第 t t t 时刻的词。

1.2.2 RNN 的具体运算过程

首先看一个单层的 RNN 结构：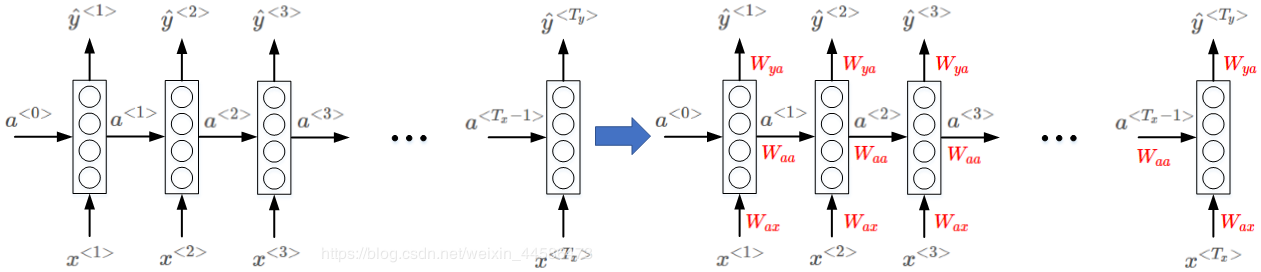
在这里插入图片描述那么大家可能会产生疑问：这里看起来不是已经好多层了吗？怎么还是单层的？—— 其实，这就是 RNN 有别于 DNN, CNN 的一点了， RNN 的拓扑结构发生了很大的改变。我们需要明确一点：对于 RNN 而言，横向对齐的就视为同一层—— 这是因为：这一层所有的参数都是共享的！

既然谈到了参数，那么我们就有必要看看 RNN 是如何进行前向传播的：

RNN 需要有两个输入：

  1. 原本该时刻的单词输入 x < t > x^{} x
  2. 上一个时刻的激活值（或者说隐藏值） a < t − 1 > a^{} a

我们这里的矩形框代表了类似于 DNN 里面的一个隐藏层，它执行的是下面的计算过程：
a < t > = t a n h ( W a a a < t − 1 > + W a x x < t > + b a ) y < t > = g ( W y a a < t > + b y ) a^{} = tanh(W_{aa}a^{} + W_{ax}x^{} + b_a)\\ \space\\ y^{}=g(W_{ya}a^{}+b_y) a=tanh(Waaa+Waxx+ba)y=g(Wyaa+by)

那么，对于第一个时刻的输入，它确实有 x < 1 > x^{<1>} x<1>，但是此时并没有上一个时刻的激活值 a < 0 > a^{<0>} a<0>（因为现在就是第一个时刻）。此时我们可以给 a < 0 > a^{<0>} a<0> 赋值成 0 向量作为输入）

下面我们就以对句子： H a r r y P o t t e r a n d H e r m i o n e G r a n g e r i n v e n t e d a n e w s p e l l Harry\space\space Potter\space\space and\space\space Hermione\space\space Granger\space\space invented\space\space a\space\space new\space\space spell HarryPotterandHermioneGrangerinventedanewspell

进行名字识别为例，假设我们对每一个词用 10000x1 的词汇表进行独热编码，那么很容易想到，我们整个句子就是一个 10000 x 9 的矩阵： [ 0 0 ⋯ 1 0 0 0 0 ⋯ 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ 1 0 ⋯ 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ 0 1 ⋯ 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ] \begin{bmatrix} 0 & 0 & \cdots & 1 &0 & 0\\ 0 & 0 & \cdots & 0 & 0 & 0\\ \vdots & \vdots & & \vdots & \vdots & \vdots\\ 1 & 0 &\cdots &0 & 0 & 0\\ \vdots & \vdots & & \vdots & \vdots & \vdots\\ 0 & 1 &\cdots &0 & 0 &0\\ \vdots & \vdots & & \vdots & \vdots & \vdots\\ \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡00⋮1⋮0⋮00⋮0⋮1⋮⋯⋯⋯⋯10⋮0⋮0⋮00⋮0⋮0⋮00⋮0⋮0⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤

假设我们的权值 W a x W_{ax} Wax 是一个维度为 100 x 10000 的矩阵。我们设 激活值的维度是 100 x 100， W a a W_{aa} Waa 的维度也是 100 x 100。根据式子： a < t > = t a n h ( W a a a < t − 1 > + W a x x < t > + b a ) a^{} = tanh(W_{aa}a^{} + W_{ax}x^{} + b_a) a=tanh(Waaa+Waxx+ba)

如果我们把这两个权值合并为一个： W a W_a Wa，那么这个 W a W_a Wa 其实就是 W a a W_{aa} Waa 和 W a x W_{ax} Wax 的合并。合并方法就是水平合并： W a a = [ W a a ∣ W a x ] W_{aa} = [W_{aa} \quad|\quad W_{ax}] Waa=[Waa∣Wax]
如果我们把输入也合并成一个矩阵，那么应该是纵向合并： [ a < t − 1 > — — x < t > ] \begin{bmatrix} a^{}\\ ——\\ x^{} \end{bmatrix} ⎣⎡a——x⎦⎤
这样一来，我们 RNN 的激活值输出就可以简化地表示成： a < t > = W a X + b a a^{} = W_aX+b_a a=WaX+ba

看到这儿，可能大家又会有疑问了：RNN 的输出 y < t > y^{} y 呢？它怎么办？

我们现在就画出 RNN 一次前向传播完整的计算图：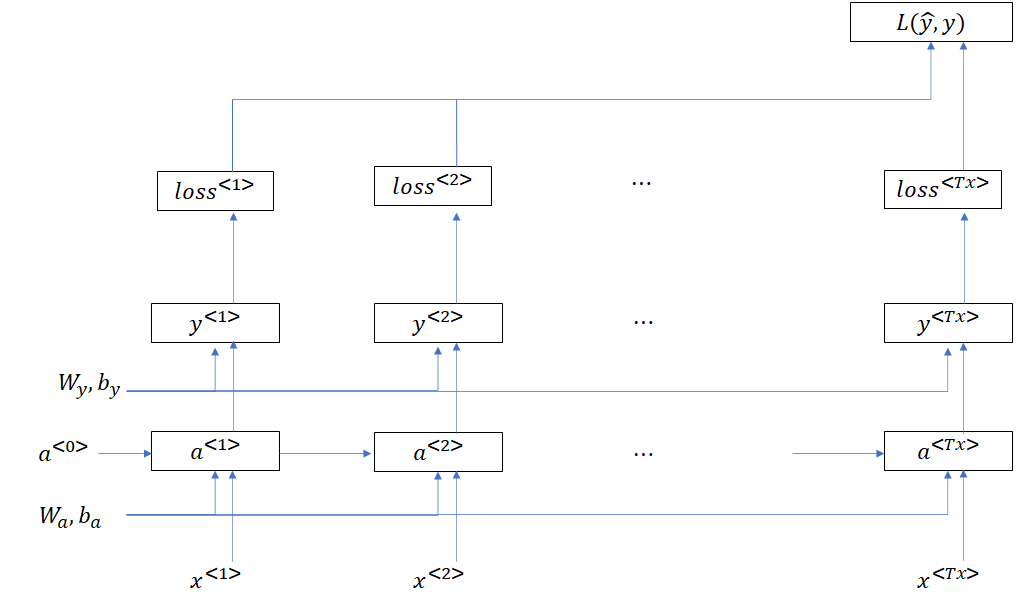
在这里插入图片描述

1.2.3 几种不同类型的 RNN

我们上面所讨论的是输入长度 T x T_x Tx 等于输出长度 T y T_y Ty 的情况，当然 也有 T x T_x Tx 不等于 T y T_y Ty 的情况——例如：多对多、多对一、一对多、一对一等等情况。我们可以根据需要再深入学习。

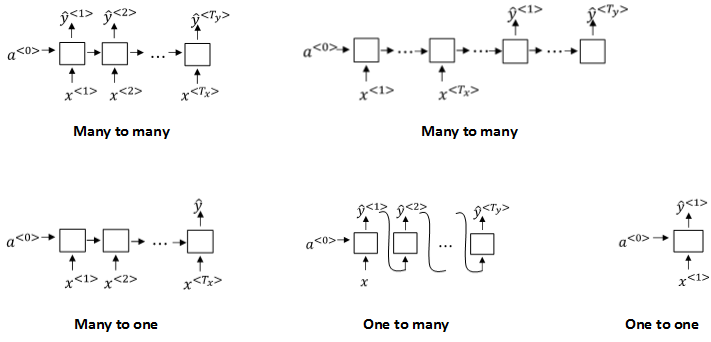
20200405185858194.png

二、基于Pytorch的RNN实践部分

2.1 在Pytorch里面对 RNN 输入参数的认识

Pytorch 里面为我们封装好了 n n . R N N nn.RNN nn.RNN，每次向网络中输入batch个样本，每个时刻处理的是该时刻的 batch 个样本。我们首先来看看 Pytorch 里面 n n . R N N nn.RNN nn.RNN 的参数：

  1. i n p u t _ s i z e input\_size input_size ：输入 x x x 的特征大小，比如说我们刚刚用一个 10000 x 1的词汇库去表示一个句子里面的其中一个词，所以，此时的 i n p u t _ s i z e input\_size input_size 就是 10000
  2. h i d d e n _ s i z e hidden\_size hidden_size： 可以理解为隐藏层神经元的数目
  3. n u m _ l a y e r s num\_layers num_layers： RNN 里面层的数量
  4. n o n l i n e a r i t y nonlinearity nonlinearity： 激活函数，默认为 t a n h tanh tanh，可以设置为 r e l u relu relu
  5. b i a s bias bias： 是否设置偏置，默认为 T r u e True True
  6. b a t c h _ f i r s t batch\_first batch_first： 默认为 f a l s e false false, 设置为 T r u e True True 之后，输入输出为 ( b a t c h _ s i z e , s e q _ l e n , i n p u t _ s i z e ) (batch\_size, seq\_len, input\_size) (batch_size,seq_len,input_size)
  7. d r o p o u t dropout dropout： 默认为0（当层数较多，神经元数目较多时， d r o p o u t dropout dropout 特别有用）
  8. b i d i r e c t i o n a l bidirectional bidirectional： 默认为 F a l s e False False ， T r u e True True 则设置 RNN 为双向

上面的参数介绍里面提到了几个词： b a t c h _ s i z e , s e q _ l e n , i n p u t _ s i z e batch\_size, seq\_len, input\_size batch_size,seq_len,input_size 这该怎么理解呢？

比如说，我们还是以找寻句子里面的人名为例，但是这次的情况是：我一次给 RNN 输入3句话，每句话10个单词，每个单词用 10000维 的向量（10000 行的词汇表）表示。那么对应的 b a t c h _ s i z e batch\_size batch_size 就是 3； s e q _ l e n seq\_len seq_len 就是 10 ； i n p u t _ s i z e input\_size input_size 就是 10000.（值得注意的是： a e q _ l e n aeq\_len aeq_len 应该就是 RNN 的时间步）

说到这里，我们再举一个例子：

  1. self.rnn = nn.RNN(
  2.             input_size=INPUT_SIZE,
  3.             hidden_size=32,     # rnn hidden unit
  4.             num_layers=1,       # number of rnn layer
  5.             batch_first=True,   # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
  6.         )

这样，我们就定义好了一个 RNN 层。

2.2 nn.RNN 里面的 forward 方法：

在对 RNN 进行前向传播时，注意这里调用的不是我们自己写的 f o r w a r d forward forward，而是 Pytorch里面 nn.RNN 的方法。具体格式如下：

  1. rnn_out, h_state = self.rnn(x, h_state)

输入的第一参数 x x x ，它是一次性将所有时刻特征喂入的，而不需要每次喂入当前时刻的 x < t > x^{} x，所以其 s h a p e shape shape 是 [ b a t c h _ s i z e , s e q _ l e n , i n p u t _ s i z e ] [batch\_size, seq\_len, input\_size] [batch_size,seq_len,input_size]

输入的第二参数 h _ s t a t e h\_state h_state 是第一个时刻空间上所有层的记忆单元的Tensor，，只是还要考虑循环网络空间上的层数，所以这里输入的 s h a p e shape shape 是 [ n u m _ l a y e r , b a t c h _ s i z e , h i d d e n _ s i z e ] [num\_layer,batch\_size ,hidden\_size] [num_layer,batch_size,hidden_size]

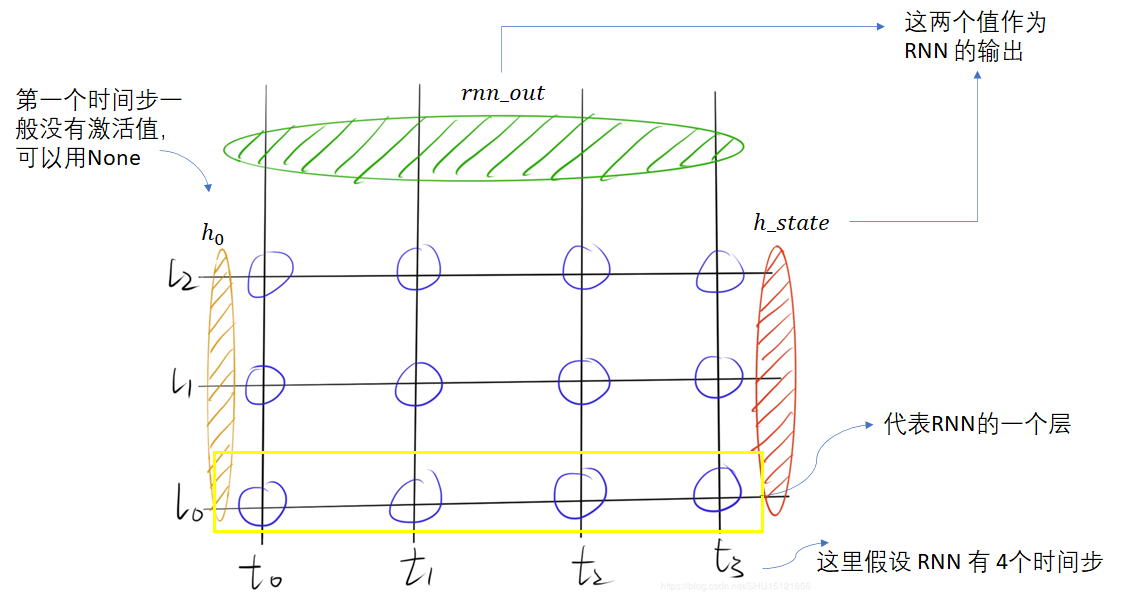
在这里插入图片描述

如上图所示，返回值有两个 r n n _ o u t rnn\_out rnn_out 和 h _ s t a t e h\_state h_state，其中，
r n n _ o u t rnn\_out rnn_out每一个时刻上空间上最后一层的输出（但是注意：这个输出不是我们所说的 y ^ \hat{y} y^，要产生 y ^ \hat{y} y^ 还需要我们再设计一个 n n . L i n e a r nn.Linear nn.Linear），所以它的shape是 [ b a t c h _ s i z e , s e q _ l e n , h i d d e n _ s i z e ] [batch\_size, seq\_len, hidden\_size] [batch_size,seq_len,hidden_size]

h _ s t a t e h\_state h_state 是最后一个时刻空间上所有层的记忆单元，它和 h 0 h_0 h0 的维度应该是一样的： [ n u m _ l a y e r , b a t c h _ s i z e , h i d d e n _ s i z e ] [num\_layer,batch\_size ,hidden\_size] [num_layer,batch_size,hidden_size]

Example：利用RNN进时间序列的预测

在本次的例子里面，我们的目的是用 s i n sin sin 函数预测 c o s cos cos 函数。主要还是为了熟悉 RNN 关于输入输出的一些细节。那么第一步就是导入必要的包啦：

  1. import torch
  2. from torch import nn
  3. from torch.autograd import Variable
  4. import numpy as np
  5. import matplotlib.pyplot as plt

下面我们定义一些超参数：

  1. # Hyper Parameters
  2. TIME_STEP = 10      # rnn time step
  3. INPUT_SIZE = 1      # 说明一下:因为在每一个时间节上我们输入的数据就只是一个数据,并不像词那样用一个词汇表编码，所以这里input size就是1 
  4. LR = 0.02           # learning rate

展示一下我们的数据：

  1. # show data
  2. steps = np.linspace(0, np.pi*2, 100, dtype=np.float32)  # float32 for converting torch FloatTensor
  3. x_np = np.sin(steps)
  4. y_np = np.cos(steps)
  5. plt.plot(steps, y_np, 'r-', label='target (cos)')
  6. plt.plot(steps, x_np, 'b-', label='input (sin)')
  7. plt.legend(loc='best')
  8. plt.show()

下面是重点部分：我们开始构造我们的 RNN model：下面细节的解释都会在注释里面

  1. class RNN(nn.Module):
  2.     def __init__(self):
  3.         super(RNN, self).__init__()
  5.         self.rnn = nn.RNN(
  6.             input_size=INPUT_SIZE,
  7.             hidden_size=32,     # rnn hidden unit
  8.             num_layers=1,       # number of rnn layer
  9.             batch_first=True,   # input & output will has batch size as 1s dimension. e.g. (batch, time_step, input_size)
  10.         )
  11.         self.out = nn.Linear(32, 1)   #说明：这里是 RNN 之外再加入的一个全连接层
  13.     def forward(self, x, h_state):
  14.         # x（输入）的维度就是(batch, time_step, input_size)
  15.         # h_state (n_layers, batch, hidden_size)
  16.         # r_out (batch, time_step, hidden_size)
  17.         r_out, h_state = self.rnn(x, h_state)  #注意：这里调用了nn.RNN的forward方法，输出两个，请看上文对它们的解释
  18.         #print('第step次迭代, RNN所有时间结点上隐藏层的输出维度:', r_out.size())   #[batch, seq_len, hidden_len]
  20.         outs = []    # save all predictions 这里我们需要定义一个空的列表，用于存放每一个时间节真正的输出（而不是r_out)
  21.         for time_step in range(r_out.size(1)):    # calculate output for each time step r_out.size(1)seq_len也即是时间节的长度
  22.             outs.append(self.out(r_out[:, time_step, :]))  #这里用[:, time_step,:]取出第time_step时刻的r_out作为nn.Linear的输入，用于计算该时刻真正的输出
  23.         return torch.stack(outs, dim=1), h_state  #最后我们需要把每一个时间节得到的output按照第二个维度拼起来

好的，在搞清楚 Pytorch 里面 RNN 的输入输出以及前向传播的计算过程之后，我们就要开始训练了：

  1. rnn = RNN()
  3. optimizer = torch.optim.Adam(rnn.parameters(), lr=LR)   # optimize all cnn parameters
  4. loss_func = nn.MSELoss()
  6. h_state = None      # for initial hidden state 因为第1个时间节没有前一时刻的激活值，这里我们可以用None作为输入
  8. plt.figure(1, figsize=(12, 5))
  9. plt.ion()           # continuously plot
  11. for step in range(100):    #训练100代
  12.     start, end = step * np.pi, (step+1)*np.pi   # time range
  13.     # use sin predicts cos
  14.     steps = np.linspace(start, end, TIME_STEP, dtype=np.float32, endpoint=False)  # float32 for converting torch FloatTensor
  15.     x_np = np.sin(steps)
  16.     y_np = np.cos(steps)
  18.     x = Variable(torch.from_numpy(x_np[np.newaxis, :, np.newaxis]))    # shape (batch, time_step, input_size) 给 x_np加上第一个和第三个维度，都是1，因为这里默认batch = 1, input_size=1
  19.     #print('x的维度:', x.shape)   [1, 10, 1]
  20.     y = Variable(torch.from_numpy(y_np[np.newaxis, :, np.newaxis]))
  21.     #print('y的维度:', y.shape)  [1, 10, 1]
  23.     prediction, h_state = rnn(x, h_state) 
  25.     #Be careful!!!!#####
  26.     h_state = Variable(h_state.data)        # repack the hidden state, break the connection from last iteration 
  27.     #上面这一步我们需要把 RNN 第n次迭代生成的激活值作为下一代训练里面的 h0 输入，要重新打包成 Variable
  29.     loss = loss_func(prediction, y)         # calculate loss
  30.     optimizer.zero_grad()                   # clear gradients for this training step
  31.     loss.backward()                         # backpropagation, compute gradients
  32.     optimizer.step()                        # apply gradients
  34.     #plotting
  35.     plt.plot(steps, y_np.flatten(), 'r-')
  36.     plt.plot(steps, prediction.data.numpy().flatten(), 'b-')
  37.     plt.draw(); 
  38.     plt.pause(0.05)
  40. plt.ioff()
  41. plt.show()

至此，我们应该对 RNN 的工作机理有了一个较为深入的了解。但是，在实际工程中，数据清洗与数据集的制作将会远远难于 RNN 本身的构造。这也需要我们有一个较深入的编程能力。虽然 Pytorch 等深度学习框架可以如此方便地自动计算梯度等等，但是数据集制作效果的好坏直接影响了我们 m o d e l model model 的表现。

然而，你以为故事到这儿就结束了吗？

如果我们现在的工作是让机器填词：假设我们给机器输入这样一段话： I a m C h i n e s e ⋯ ( 1000 w o r d s l a t e r ) ⋯ I c a n s p e a k f l u e n t _ _ _ _ _ I \space\space am\space\space Chinese \cdots (1000\space\space words\space\space later)\cdots I \space\space can \space\space speak \space\space fluent \space\space \_\_\_\_\_ IamChinese⋯(1000wordslater)⋯Icanspeakfluent_____
我们希望机器正确地填出最后一个词：当然希望是 C h i n e s e Chinese Chinese，然而假设中间这1000个词都和 C h i n e s e Chinese Chinese 没什么大关系，那么机器就需要记住句子一开始的 C h i n e s e Chinese Chinese。这无疑会给 RNN 反向传播带来极大的困难，可能会造成梯度消失。那么如何解决这个问题呢？—— 因此 L S T M LSTM LSTM 和它的变体 G R U GRU GRU 应运而生。

在之后的 B l o g Blog Blog 里面，我们会详细地学习 L S T M LSTM LSTM 的工作机理，以及如何在 P y t o r c h Pytorch Pytorch 里面实现 LSTM

发表评论

表情：
评论列表 （有 0 条评论，9人围观）

还没有评论，来说两句吧...

相关阅读