日萌社" class="reference-link">日萌社

人工智能AI：Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战（不定时更新）

Pytorch完成线性回归

目标

知道如何手动完成线性回归

1. 线性回归实现

下面，我们使用一个自定义的数据，来使用torch实现一个简单的线性回归

假设我们的基础模型就是y = wx+b，其中w和b均为参数，我们使用y = 3x+0.8来构造数据x、y，所以最后通过模型应该能够得出w和b应该分别接近3和0.8

准备数据
计算预测值
计算损失，把参数的梯度置为0，进行反向传播
更新参数

import torch
import numpy as np
from matplotlib import pyplot as plt

#1. 准备数据 y = 3x+0.8，准备参数
x = torch.rand([50])
y = 3*x + 0.8
w = torch.rand(1,requires_grad=True)
b = torch.rand(1,requires_grad=True)
def loss_fn(y,y_predict):
    loss = (y_predict-y).pow(2).mean()
    for i in [w,b]:
        #每次反向传播前把梯度置为0
        if i.grad is not None:
            i.grad.data.zero_()
    # [i.grad.data.zero_() for i in [w,b] if i.grad is not None]
    loss.backward()
    return loss.data
def optimize(learning_rate):
    # print(w.grad.data,w.data,b.data)
    w.data -= learning_rate* w.grad.data
    b.data -= learning_rate* b.grad.data
for i in range(3000):
    #2. 计算预测值
    y_predict = x*w + b
    #3.计算损失，把参数的梯度置为0，进行反向传播 
    loss = loss_fn(y,y_predict)
    if i%500 == 0:
        print(i,loss)
    #4. 更新参数w和b
    optimize(0.01)
# 绘制图形，观察训练结束的预测值和真实值
predict =  x*w + b  #使用训练后的w和b计算预测值
plt.scatter(x.data.numpy(), y.data.numpy(),c = "r")
plt.plot(x.data.numpy(), predict.data.numpy())
plt.show()
print("w",w)
print("b",b)

图形效果如下：

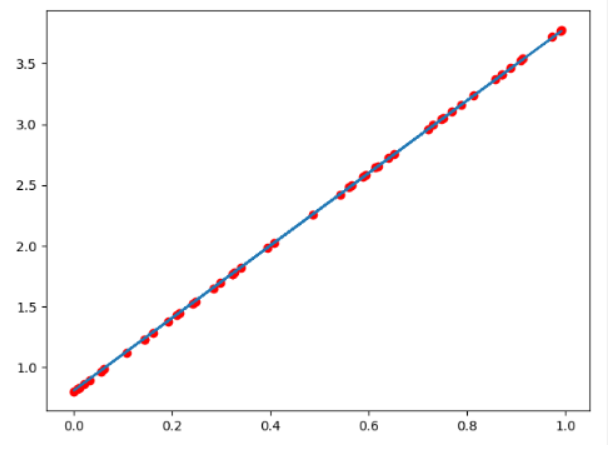
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ppbWlhbzU1MjE0NzU3Mg_size_16_color_FFFFFF_t_70

打印w和b，可有

w tensor([2.9280], requires_grad=True)
b tensor([0.8372], requires_grad=True)

可知，w和b已经非常接近原来的预设的3和0.8

Pytorch基础模型

目标

知道如何使用pytorch模型组件构建模型
知道如何在GPU上运行代码
能够说出常见的优化器及其原理

1 使用pytorch模型组件把线性回归完整代码

构建模型，最重要的有两个步骤：

找到合适的计算关系，随即初始化参数来拟合输入和输出的关系（前向计算，从输入得到输出）
选取合适的损失函数和优化器来减小损失（反向传播，得到合适的参数）

import torch
from torch import nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt

1. 定义数据
x = torch.rand([50,1])
y = x*3 + 0.8

2 .定义模型
class Lr(nn.Module):
```
def __init__(self):
    super(Lr,self).__init__()
    self.linear = nn.Linear(1,1)
def forward(self, x):
    out = self.linear(x)
    return out
```
2. 实例化模型，loss，和优化器
model = Lr()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)

3. 训练模型
for i in range(30000):
```
out = model(x) #3.1 获取预测值
loss = criterion(y,out) #3.2 计算损失
optimizer.zero_grad()  #3.3 梯度归零
loss.backward() #3.4 计算梯度
optimizer.step()  # 3.5 更新梯度
if (i+1) % 20 == 0:
    print('Epoch[{}/{}], loss: {:.6f}'.format(i,30000,loss.data))
```
4. 模型评估
model.eval() #设置模型为评估模式，即预测模式
predict = model(x)
predict = predict.data.numpy()
plt.scatter(x.data.numpy(),y.data.numpy(),c=”r”)
plt.plot(x.data.numpy(),predict)
plt.show()

输出如下：

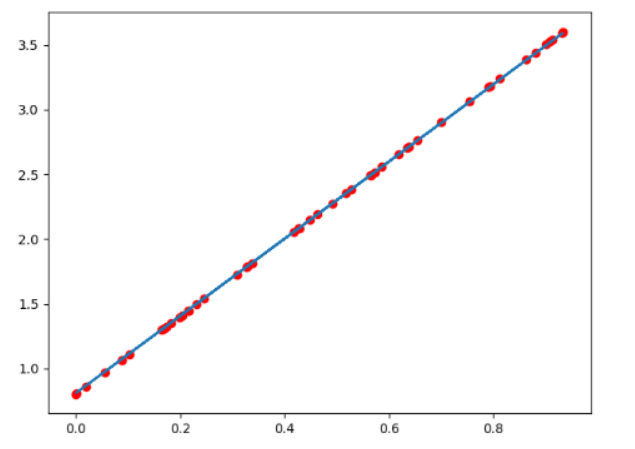
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3ppbWlhbzU1MjE0NzU3Mg_size_16_color_FFFFFF_t_70 1

注意：

model.eval()表示设置模型为评估模式，即预测模式

model.train(mode=True) 表示设置模型为训练模式

在当前的线性回归中，上述并无区别

但是在其他的一些模型中，训练的参数和预测的参数会不相同，到时候就需要具体告诉程序我们是在进行训练还是预测，比如模型中存在Dropout，BatchNorm的时候

2. 在GPU上运行代码

当模型太大，或者参数太多的情况下，为了加快训练速度，经常会使用GPU来进行训练

此时我们的代码需要稍作调整：

判断GPU是否可用torch.cuda.is_available()

torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
>>device(type='cuda', index=0)  #使用gpu
>>device(type='cpu') #使用cpu

把模型参数和input数据转化为cuda的支持类型
```
model.to(device)
x_true.to(device)
```
在GPU上计算结果也为cuda的数据类型，需要转化为numpy或者torch的cpu的tensor类型
```
predict = predict.cpu().detach().numpy()
```
detach()的效果和data的相似，但是detach()是深拷贝，data是取值，是浅拷贝

修改之后的代码如下：

import torch
from torch import nn
from torch import optim
import numpy as np
from matplotlib import pyplot as plt
import time
# 1. 定义数据
x = torch.rand([50,1])
y = x*3 + 0.8
#2 .定义模型
class Lr(nn.Module):
    def __init__(self):
        super(Lr,self).__init__()
        self.linear = nn.Linear(1,1)
    def forward(self, x):
        out = self.linear(x)
        return out
# 2. 实例化模型，loss，和优化器
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
x,y = x.to(device),y.to(device)
model = Lr().to(device)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
#3. 训练模型
for i in range(300):
    out = model(x)
    loss = criterion(y,out)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    if (i+1) % 20 == 0:
        print('Epoch[{}/{}], loss: {:.6f}'.format(i,30000,loss.data))
#4. 模型评估
model.eval() #
predict = model(x)
predict = predict.cpu().detach().numpy() #转化为numpy数组
plt.scatter(x.cpu().data.numpy(),y.cpu().data.numpy(),c="r")
plt.plot(x.cpu().data.numpy(),predict,)
plt.show()