LeetCode（Queue)950. Reveal Cards In Increasing Order

我就是我 2023-09-25 19:08 62阅读 0赞

# 1.问题 #

You are given an integer array deck. There is a deck of cards where every card has a unique integer. The integer on the ith card is deck\[i\].

You can order the deck in any order you want. Initially, all the cards start face down (unrevealed) in one deck.

You will do the following steps repeatedly until all cards are revealed:

Take the top card of the deck, reveal it, and take it out of the deck.  
If there are still cards in the deck then put the next top card of the deck at the bottom of the deck.  
If there are still unrevealed cards, go back to step 1. Otherwise, stop.  
Return an ordering of the deck that would reveal the cards in increasing order.

Note that the first entry in the answer is considered to be the top of the deck.

Example 1:

> Input: deck = \[17,13,11,2,3,5,7\]  
> Output: \[2,13,3,11,5,17,7\]  
> Explanation:  
> We get the deck in the order \[17,13,11,2,3,5,7\] (this order does not matter), and reorder it.  
> After reordering, the deck starts as \[2,13,3,11,5,17,7\], where 2 is the top of the deck.  
> We reveal 2, and move 13 to the bottom. The deck is now \[3,11,5,17,7,13\].  
> We reveal 3, and move 11 to the bottom. The deck is now \[5,17,7,13,11\].  
> We reveal 5, and move 17 to the bottom. The deck is now \[7,13,11,17\].  
> We reveal 7, and move 13 to the bottom. The deck is now \[11,17,13\].  
> We reveal 11, and move 17 to the bottom. The deck is now \[13,17\].  
> We reveal 13, and move 17 to the bottom. The deck is now \[17\].  
> We reveal 17.  
> Since all the cards revealed are in increasing order, the answer is correct.

Example 2:

> Input: deck = \[1,1000\]  
> Output: \[1,1000\]

Constraints:

*  1 <= deck.length <= 1000
 *  1 <= deck\[i\] <= 106  
    All the values of deck are unique.

# 2. 解题思路 #

**问题说明：**

> 桌子上有一副牌（a deck of cards），面朝下扣着，翻开第一张，然后拿走，并且把其后的一张牌放到这副牌的最下面，以此类推，直到把所有牌都翻开。求这副牌开始应该以什么顺序放，可以保证把所有牌翻开后，是有序的。  
> **具体解释：**  
> 目的是根据一组随机排列的数字，模拟一种洗牌和排序的操作，并最终将这些数字以递增顺序返回。  
> 以下是该问题的具体描述：  
> 给定一组随机排列的数字，例如 \[2, 13, 3, 11, 5, 17\]，你需要模拟以下操作：  
> 从牌堆顶部取出一张牌，将其放入一个新的数组中；  
> 再从牌堆顶部取出一张牌，将其放入牌堆的底部；  
> 重复上述步骤，直到牌堆为空。  
> 最终返回的数组需要以递增顺序排列，例如对于上述示例，输出应为 \[2, 3, 5, 11, 13, 17\]。

## 方法1： ##

> 1.获取牌堆的大小  
> 2.将输入数组进行排序  
> 3.创建一个队列 q，用于记录当前牌堆中每张牌的位置  
> 4.将 0 到 n-1 的数字依次加入队列中，表示牌堆中每张牌的位置  
> 5.创建一个长度为 n 的数组 res，用于存储最终排序后的结果  
> 6.从队列中弹出一个元素，该元素表示当前要填充的位置；将当前的牌放入该位置，并记录在 res 数组中  
> 7.将队列的左侧元素弹出，并将其放回队列的右侧，模拟将一张牌放到牌堆的底部的操作  
> 8.返回排序后的数组 res

## 方法2： ##

> 1.获取牌堆的大小  
> 2.将输入数组进行排序  
> 3.创建一个队列 q，用于存储排序后的结果  
> 4.如果队列不为空，将队首元素移到队尾  
> 5.将当前牌插入队首  
> 6.创建一个长度为 n 的数组 res，用于存储最终结果  
> 7.从队列中弹出元素，并将其存储在 res 数组中  
> 8.返回排序后的数组 res

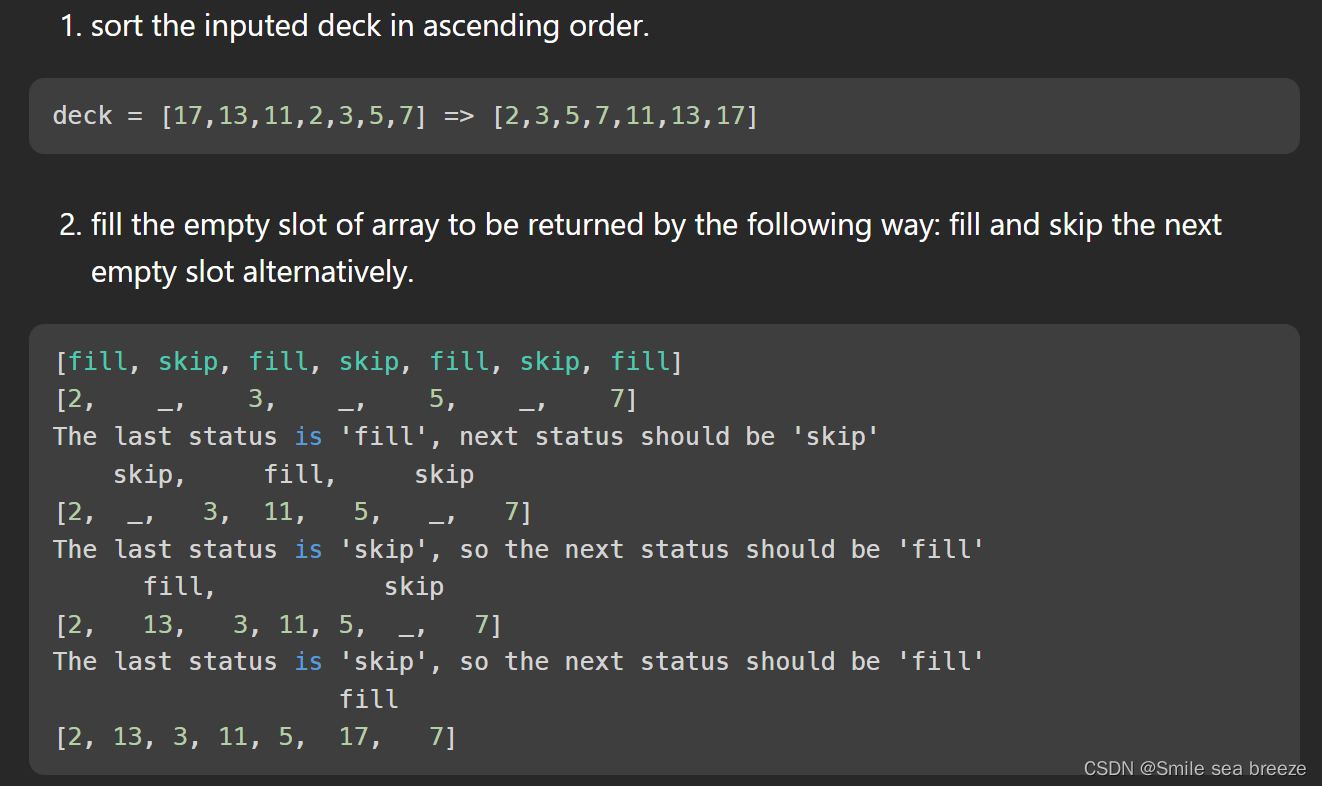
## 方法3： ##

> 1.对输入数组进行排序  
> 2.创建一个长度为 deck.length 的数组 res，用于存储最终结果  
> 3.创建一个长度为 deck.length 的布尔数组 filled，用于标记每个位置是否已经被填充  
> 4.标记当前位置是否需要跳过  
> 5.创建两个指针 i 和 j，用于遍历牌堆和结果数组  
> 6.如果当前位置已经被填充，则将 j 指向下一个位置  
> 7.如果当前位置需要跳过，则将 skip 标记置为 false  
> 8.否则将当前牌插入结果数组的 j 位置，并将 filled\[j\] 标记置为 true  
> 9.将 j 指向下一个位置  
> 10.返回结果数组 res

# 3. 代码 #

## 代码1： ##

class Solution {
        
        public int[] deckRevealedIncreasing(int[] deck) {
        
            int n = deck.length;  // 1.获取牌堆的大小
            Arrays.sort(deck);  // 2.将输入数组进行排序
            Queue<Integer> q = new LinkedList<>();  // 3.创建一个队列 q，用于记录当前牌堆中每张牌的位置
            for (int i = 0; i < n; i++) {
        
                q.add(i);  // 4.将 0 到 n-1 的数字依次加入队列中，表示牌堆中每张牌的位置
            }
            int[] res = new int[n];  // 5.创建一个长度为 n 的数组 res，用于存储最终排序后的结果
            for (int i = 0; i < n; i++) {
        
                // 6.从队列中弹出一个元素，该元素表示当前要填充的位置；将当前的牌放入该位置，并记录在 res 数组中
                res[q.poll()] = deck[i];
                // 7.将队列的左侧元素弹出，并将其放回队列的右侧，模拟将一张牌放到牌堆的底部的操作
                q.add(q.poll());
            }
            return res;  // 8.返回排序后的数组 res
        }
    }

## 代码2： ##

class Solution {
        
        public int[] deckRevealedIncreasing(int[] deck) {
        
            int n = deck.length;  // 1.获取牌堆的大小
            Arrays.sort(deck);  // 2.将输入数组进行排序
            Queue<Integer> q = new LinkedList<>();  // 3.创建一个队列 q，用于存储排序后的结果
            for (int i = n - 1; i >= 0; --i) {
        
                if (q.size() > 0) q.add(q.poll());  // 4.如果队列不为空，将队首元素移到队尾
                q.add(deck[i]);  // 5.将当前牌插入队首
            }
            int[] res = new int[n];  // 6.创建一个长度为 n 的数组 res，用于存储最终结果
            for (int i = n - 1; i >= 0; --i) {
        
                res[i] = q.poll();  // 7.从队列中弹出元素，并将其存储在 res 数组中
            }
            return res;  // 8.返回排序后的数组 res
        }
    }

## 代码3： ##

class Solution {
        
        public int[] deckRevealedIncreasing(int[] deck) {
        
            Arrays.sort(deck);  // 1.对输入数组进行排序
            int[] res = new int[deck.length];  // 2.创建一个长度为 deck.length 的数组 res，用于存储最终结果
            boolean[] filled = new boolean[deck.length];  // 3.创建一个长度为 deck.length 的布尔数组 filled，用于标记每个位置是否已经被填充
            boolean skip = false;  // 4.标记当前位置是否需要跳过
            int i = 0, j = 0;  // 5.创建两个指针 i 和 j，用于遍历牌堆和结果数组
            while(i < deck.length) {
        
                if(filled[j]) {
          // 6.如果当前位置已经被填充，则将 j 指向下一个位置
                    j = (j + 1) % deck.length;
                    continue;
                }
    
                if(skip) {
          // 7.如果当前位置需要跳过，则将 skip 标记置为 false
                    skip = false;
                } else {
          // 8.否则将当前牌插入结果数组的 j 位置，并将 filled[j] 标记置为 true
                    res[j] = deck[i++];
                    filled[j] = true;
                    skip = true;
                }
                j = (j + 1) % deck.length;  // 9.将 j 指向下一个位置
            }
    
            return res;  // 10.返回结果数组 res
        }
    }

![在这里插入图片描述][6fcef7a6a9624976925136e6ec46b8b5.png]  
[参考][Link 1]

## 代码4： ##

> 和代码1思路相同，不同的是使用了非双端队列  
> `非双端队列（non-deque）`是指只能在队列的一端插入元素，另一端删除元素的队列，也称为普通队列。  
> 在这种队列中，元素只能按照它们进入队列的顺序进行处理。在 Java 中，非双端队列通常使用 Queue 接口进行实现。LinkedList 类就是一种实现了 Queue 接口的非双端队列。其他常见的非双端队列包括 ArrayBlockingQueue 和 PriorityQueue 等。

class Solution {
        
        public int[] deckRevealedIncreasing(int[] deck) {
        
        // 获取牌堆的大小
            int n = deck.length;
            // 创建一个长度为 n 的数组 res，用于存储最终排序后的结果
            int[] res = new int[n];
            // 创建一个长度为 n 的双端队列 queue，用于记录当前牌堆中每张牌的位置
            Deque<Integer> queue = new LinkedList<>();
            // 将 0 到 n-1 的数字依次加入队列中，表示牌堆中每张牌的位置
            for (int i = 0; i < n; i++) {
        
                queue.offer(i);
            }
            // 将输入数字数组进行排序
            Arrays.sort(deck);
            // 遍历排序后的数字数组，依次将每张牌放入 res 数组中
            for (int card : deck) {
        
                // 从队列中弹出一个元素，该元素表示当前要填充的位置；将当前的牌放入该位置，并记录在 res 数组中
                res[queue.poll()] = card;
                // 如果队列非空，即还有牌需要处理，将队列的左侧元素弹出，并将其放回队列的右侧，模拟将一张牌放到牌堆的底部的操作
                if (!queue.isEmpty()) {
        
                    queue.offer(queue.poll());
                }
            }
            // 返回排序后的数组 res
            return res;
        }
    }

[6fcef7a6a9624976925136e6ec46b8b5.png]: https://img-blog.csdnimg.cn/6fcef7a6a9624976925136e6ec46b8b5.png
[Link 1]: https://leetcode.com/problems/reveal-cards-in-increasing-order/solutions/504896/java-solution-without-queue/?q=java&orderBy=most_votes