LeetCode（Stack)897. Increasing Order Search Tree

分手后的思念是犯贱 2023-09-25 22:48 63阅读 0赞

# 1.问题 #

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1: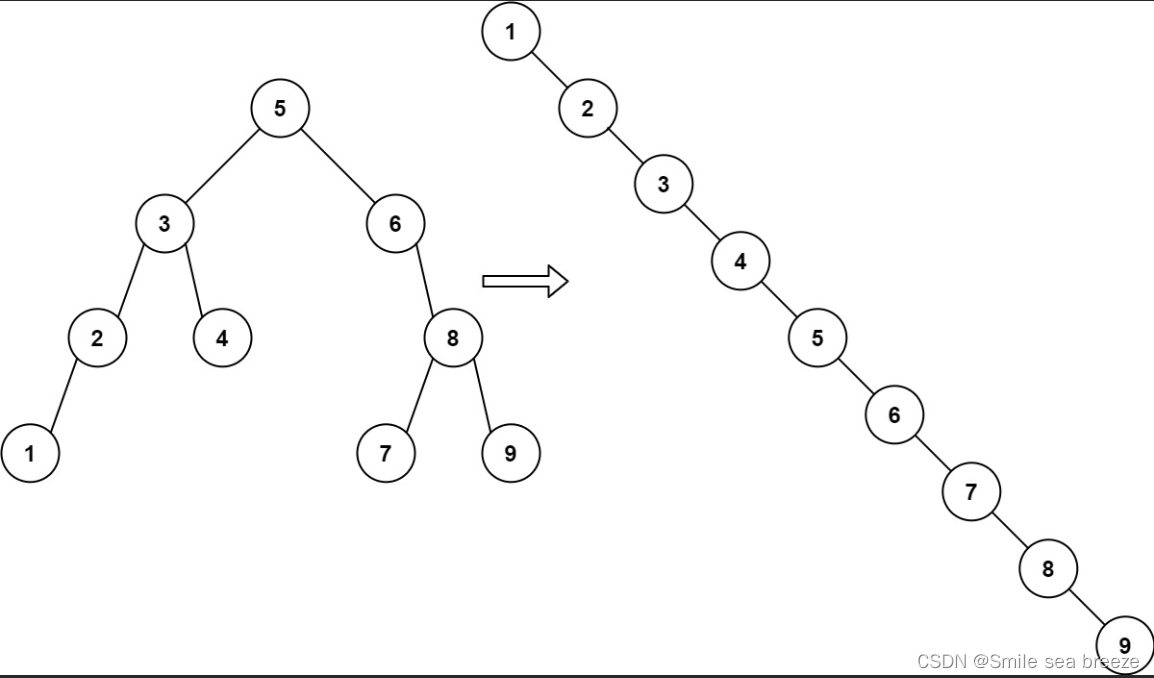  
![在这里插入图片描述][484b807f5b6744de821dee49d8e3514a.png]

> Input: root = \[5,3,6,2,4,null,8,1,null,null,null,7,9\]  
> Output: \[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9\]

Example 2:  
![在这里插入图片描述][a2e70c5481613ebb9759d52a9134188f.jpeg_pic_center]

Input: root = \[5,1,7\]  
Output: \[1,null,5,null,7\]

Constraints:

*  The number of nodes in the given tree will be in the range \[1, 100\].
 *  0 <= Node.val <= 1000

# 2. 解题思路 #

## 方法1： ##

> 对于每个节点，我们将其右子树作为单链表返回，并将其作为链表的最后一个节点。

1.对于根节点 root，将其左子树转化为只包含右子树的单链表，并将其右子树转化为只包含右子树的单链表。  
2.将左子树转化后的单链表接到根节点后面，并将根节点的左子树置为空。  
3.如果右子树转化后的单链表不为空，将其接到根节点后面。  
返回根节点。

*  时间复杂度：O(n)，其中 n 是二叉搜索树中的节点数，需要遍历所有节点一次。
 *  空间复杂度：O(h)，其中 h 是二叉搜索树的高度，需要递归 h 层，因此需要使用 O(h) 的栈空间。

## 方法2： ##

> 这道题可以使用中序遍历将二叉搜索树的所有节点按从小到大的顺序存储到一个 ArrayList 中，然后再根据 ArrayList 中的值构建一棵只包含右子树的二叉树。由于二叉搜索树的中序遍历结果是有序的，因此我们可以保证新构建的二叉树也是有序的。

具体思路如下：

1.创建一个 ArrayList，用于存储中序遍历结果。  
2.创建一个栈，用于遍历二叉搜索树。  
3.初始化当前节点为根节点。  
4.当当前节点不为空或栈不为空时，进行以下操作：  
a. 将左子树中的所有节点压入栈中。  
b. 弹出栈顶元素，即为最左侧的叶子节点。  
c. 将当前节点的值加入 ArrayList 中。  
d. 处理右子树。  
5.新建一个根节点，并用一个指针 p 指向根节点。  
6.遍历 ArrayList 中的元素：  
a. 创建一个新的节点，并将值赋为当前元素。  
b. 将指针 p 指向新创建的节点。  
7.返回根节点的右子树，即为转化后的单链表。

# 3. 代码 #

## 代码1： ##

class Solution {
        
        public TreeNode increasingBST(TreeNode root) {
        
            return convert(root, null); // 将原始的根节点作为参数传入 convert 方法，并将尾节点置为空，即可得到只包含右子树的单链表的根节点
        }
    
        private TreeNode convert(TreeNode root, TreeNode tail) {
        
            if (root == null) {
         // 递归到了空节点，返回尾节点
                return tail;
            }
            TreeNode res = convert(root.left, root); // 先递归处理左子树，并将根节点 root 作为链表的最后一个节点
            root.left = null; // 将根节点 root 的左子树置为空
            root.right = convert(root.right, tail); // 将右子树转化为只包含右子树的单链表，并将其接到 root 后面
            return res; // 返回转化后的单链表的头节点
        }
    }

> 根据中序遍历的结果，放入新建一个根节点，并用一个指针 p 指向根节点。根节点的右子树，即为转化后的单链表。

/**
     * Definition for a binary tree node.
     * public class TreeNode {
     *     int val;
     *     TreeNode left;
     *     TreeNode right;
     *     TreeNode() {}
     *     TreeNode(int val) { this.val = val; }
     *     TreeNode(int val, TreeNode left, TreeNode right) {
     *         this.val = val;
     *         this.left = left;
     *         this.right = right;
     *     }
     * }
     */
    class Solution {
        
        List<Integer> list = new ArrayList<>();
        public TreeNode increasingBST(TreeNode root) {
        
             // 如果左子树不为空，则递归遍历左子树
            if(root.left !=null) increasingBST(root.left); 
            // 将当前节点的值加入列表
            list.add(root.val);
            // 如果右子树不为空，则递归遍历右子树
            if(root.right !=null) increasingBST(root.right);
           
            TreeNode newRoot = new TreeNode(0); // 新建一个根节点
            TreeNode p = newRoot;
            for (int val : list) {
        
                p.right = new TreeNode(val); // 将 ArrayList 中的值依次赋值给根节点的右子树
                p = p.right;
            }
            return newRoot.right;
            
        }
    }

> 1.首先定义一个 TreeNode 类型的变量 prev 作为前一个节点，ans 作为答案节点。  
> 2.进入 increasingBST 方法，如果当前节点 node 为空，则返回 null。  
> 递归处理左子树 increasingBST(node.left)。  
> 3.如果答案节点 ans 为空，则当前节点 node 是答案节点，将其赋值给 ans。否则，将前一个节点 prev 的右子树指向当前节点 node，将当前节点 node 设为前一个节点 prev。  
> 4.将当前节点 node 的左子树置为空。  
> 5.递归处理右子树 increasingBST(node.right)。  
> 6.返回答案节点 ans。

class Solution {
        
        TreeNode prev; // 定义一个 TreeNode 类型的变量 prev 作为前一个节点
        TreeNode ans; // 定义答案节点
    
        public TreeNode increasingBST(TreeNode node) {
        
            if (node == null) {
         // 如果当前节点 node 为空，则返回 null
                return null;
            }
            
            increasingBST(node.left); // 递归处理左子树
            
            if (ans == null) {
         // 如果答案节点 ans 为空，则当前节点 node 是答案节点
                ans = node;
            } else {
         // 否则，将前一个节点 prev 的右子树指向当前节点 node，将当前节点 node 设为前一个节点 prev
                prev.right = node;
            }
            
            prev = node; // 将当前节点 node 设为前一个节点 prev
            node.left = null; // 将当前节点 node 的左子树置为空
    
            increasingBST(node.right); // 递归处理右子树
    
            return ans; // 返回答案节点
        }
    }

## 代码2： ##

class Solution {
        
        public TreeNode increasingBST(TreeNode root) {
        
            List<Integer> list = new ArrayList<>(); // 创建一个 ArrayList 用于存储中序遍历结果
            Stack<TreeNode> stack = new Stack<>(); // 创建一个栈，用于遍历二叉搜索树
            TreeNode cur = root; // 当前节点初始化为根节点
            while (cur != null || !stack.isEmpty()) {
         // 当当前节点不为空或栈不为空时
                while (cur != null) {
         // 将左子树中的所有节点压入栈中
                    stack.push(cur);
                    cur = cur.left;
                }
                cur = stack.pop(); // 弹出栈顶元素，即为最左侧的叶子节点
                list.add(cur.val); // 将当前节点的值加入 ArrayList 中
                cur = cur.right; // 处理右子树
            }
            TreeNode newRoot = new TreeNode(0); // 新建一个根节点
            TreeNode p = newRoot; // 用一个指针 p 指向根节点
            for (int val : list) {
         // 遍历 ArrayList 中的元素
                p.right = new TreeNode(val); // 创建一个新的节点，并将值赋为当前元素
                p = p.right; // 将指针 p 指向新创建的节点
            }
            return newRoot.right; // 返回根节点的右子树，即为转化后的单链表
        }
    }

[484b807f5b6744de821dee49d8e3514a.png]: https://img-blog.csdnimg.cn/484b807f5b6744de821dee49d8e3514a.png
[a2e70c5481613ebb9759d52a9134188f.jpeg_pic_center]: https://img-blog.csdnimg.cn/img_convert/a2e70c5481613ebb9759d52a9134188f.jpeg#pic_center