层次分析法

我会带着你远行 2023-09-28 14:01 227阅读 0赞

来源：数学建模清风 学习内容所整理

文章目录

  • 评价类模型
  • 层次分析法
    • 01 建立层次结构
    • 02 构建比较矩阵（判断矩阵）
    • 03 一致性检验
    • 04 权重排序
    • matlab代码实现
    • AHP的局限性

数据资料搜索网站 虫部落-快搜 https://www.chongbuluo.com/

搜索优先级：

1.谷歌搜索
2.微信搜索
3.知乎搜索

评价类模型

评价类问题中主要分为确定评价指标，形成评价体系，就是对目标打分排序选最优解。

（例如：选择哪种方案最好、哪位运 动员或者员工表现的更优秀）。

解决评价类问题先从三个问题入手：

①评价的目标是什么？

从题目要求中获取

②为了达到目标有哪些可选方案？

题目中所给可执行方案

③评价的指标是什么？

从背景材料、常识、及网上搜集的参考资料（文献）筛选合适指标

层次分析法

层次分析法（The Analytic Hierarchy Process 即 AHP）： 把问题分解成多个组成元素，又将这些因素按支配关系分别形成递阶层次节结构，通过两两比较的方法 （可以理解为冒泡排序） 确定决策方案相对重要度的总排序。

01 建立层次结构

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yitkwIaQ-1657161871582)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705150058435.png)\]

  • 目标层： 评价目标，也就是评价模型需要解决的问题
  • 准则层： 评价指标有哪些（从哪些方面来评价打分）
  • 方案层： 题目中给出的可选方法，从准则层中的指标进行权重打分排序，最终选出最优方案

使用层次分析法时，层次结构图需要放入论文中

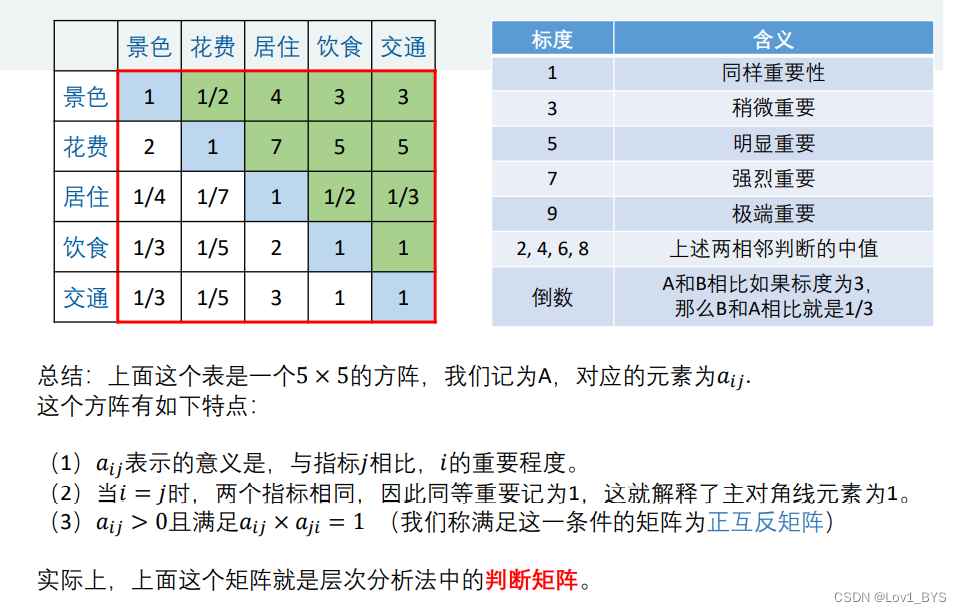
02 构建比较矩阵（判断矩阵）

  • 构建比较矩阵（判断矩阵）是为了两个两个指标进行比较，最终根据两两比较结果推算出权重构建权重表。

那如何构建比较矩阵：
在这里插入图片描述
根据上表的重要程度比较打分，比如指标一和指标二同样重要，指标三比指标一稍微重要一点，如图构建：

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NcVKViNd-1657161871585)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705160115586.png)\]
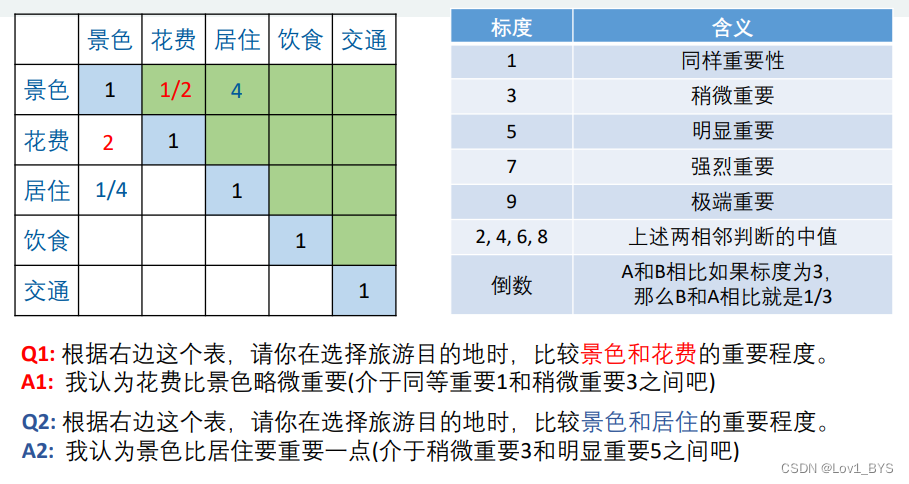
在这里插入图片描述 在这里插入图片描述

  • 什么是一致矩阵？

    \[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2JAJQFSE-1657161871587)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705194607419.png)\]
    \[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GtVU4FYc-1657161871587)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705194651187.png)\]

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kYD2mgoS-1657161871588)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705150316153.png)\]

03 一致性检验

  • 原理： 检验构造的判断矩阵和一致矩阵是否有太大区别。

  • 由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验（检验通过才能计算权重）

    一致矩阵不需要进行一致性检验，只有非一致矩阵的判断矩阵才需要进行一致性检验

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wX8H6mxt-1657161871589)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705151920869.png)\]

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4XAEedts-1657161871590)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705152132043.png)\]

04 权重排序

  • 归一化处理，计算权重

三种方法计算权重：

  1. 算术平均法
  2. 几何平均法
  3. 特征值法

特征值法最常用，但建议比赛时三种都用，避免采用单一方法所产生的偏差，得出的结论更全面、有效

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fWDmcPHr-1657161871590)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705195737705.png)\]

方法一：算术平均法求权重

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-tAaR1C67-1657161871591)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705200226299.png)\]

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hl4lXT3V-1657161871591)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705200312387.png)\]

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gbFiAKB4-1657161871592)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705200414795.png)\]

方法二：几何平均法求权重

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UwZFKWgp-1657161871593)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705200457636.png)\]

方法三：特征值法求权重

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jHgwlHN6-1657161871593)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705200539979.png)\]

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Yxlw8DKe-1657161871594)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705200557389.png)\]

matlab代码实现

  1. %% 注意：在论文写作中，应该先对判断矩阵进行一致性检验，然后再计算权重，因为只有判断矩阵通过了一致性检验，其权重才是有意义的。
  2. %% 在下面的代码中，我们先计算了权重，然后再进行了一致性检验，这是为了顺应计算过程，事实上在逻辑上是说不过去的。
  3. %% 因此大家自己写论文中如果用到了层次分析法，一定要先对判断矩阵进行一致性检验。
  4. %% 而且要说明的是，只有非一致矩阵的判断矩阵才需要进行一致性检验。
  5. %% 如果你的判断矩阵本身就是一个一致矩阵，那么就没有必要进行一致性检验。
  8. % 在每一行的语句后面加上分号(一定要是英文的哦;中文的长这个样子；)表示不显示运行结果
  9. % 多行注释:选中要注释的若干语句,快捷键Ctrl+R
  10. % 取消注释:选中要取消注释的语句,快捷键Ctrl+T
  12. disp('请输入判断矩阵A')  %matlab中disp()就是屏幕输出函数，类似于c语言中的printf（）函数
  13. % 注意，disp函数比较特殊，这里可要分号，可不要分号哦
  15. A=input('A=');
  16. % 这里输入的就是我们的判断矩阵，其为n阶方阵（行数和列数相同）
  18. % 在开始下面正式的步骤之前，我们有必要检验下A是否因为粗心而输入有误
  19. ERROR = 0;  % 默认输入是没有错误的
  21. % (1) 检查矩阵A的维数是否不大于1或不是方阵
  22. [r,c]=size(A);
  23. %size(A)函数是用来求矩阵的大小的,返回一个行向量，第一个元素是矩阵的行数，第二个元素是矩阵的列数
  24. %[r,c]=size(A)  %将矩阵A的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c
  26. if r ~= c  || r <= 1
  27.     % 注意哦，不等号是 ~=  (~是键盘Tab上面那个键，要和Shift键同时按才会出来)，别和C语言里面的!=搞混了
  28.     % ||表示逻辑运算符‘或’（在键盘Enter上面，也要和Shift键一起按） 逻辑运算符且是 && （&读and，连接符号，是and的缩写。 ）
  29.     ERROR = 1;
  30. end
  31. % Matlab的判断语句，if所在的行不需要冒号，语句的最后一定要以end结尾 ；中间的语句要注意缩进。
  33. % (2) 检验是否为正互反矩阵  a_ij > 0 且 a_ij * a_ji = 1
  34. if ERROR == 0
  35.     [n,n] = size(A);
  36.     % 因为我们的判断矩阵A是一个非零方阵，所以这里的r和c相同，我们可以就用同一个字母n表示
  37.     % 判断是否有元素小于0
  38.     %    for i = 1:n
  39.     %        for j = 1:n
  40.     %            if A(i,j)<=0
  41.     %                ERROR = 2;
  42.     %            end
  43.     %        end
  44.     %    end
  45.     if sum(sum(A <= 0)) > 0
  46.         ERROR = 2;
  47.     end
  48. end
  50. %顺便检验n是否超过了15，因为RI向量为15维
  51. if ERROR == 0
  52.     if n > 15
  53.         ERROR = 3;
  54.     end
  55. end
  57. if ERROR == 0
  58.     % 判断  a_ij * a_ji = 1 是否成立
  59.     if sum(sum(A' .* A ~=  ones(n))) > 0
  60.         ERROR = 4;
  61.     end
  62.     % A' 表示求出 A 的转置矩阵，即将a_ij和a_ji互换位置
  63.     % ones(n)函数生成一个n*n的全为1的方阵, zeros(n)函数生成一个n*n的全为0的方阵
  64.     % ones(m,n)函数生成一个m*n的全为1的矩阵
  65.     % MATLAB在矩阵的运算中，“/”号和“*”号代表矩阵之间的乘法与除法，对应元素之间的乘除法需要使用“./”和“.*”
  66.     % 如果a_ij * a_ji = 1 满足， 那么A和A'对应元素相乘应该为1
  67. end
  70. if ERROR == 0
  72.    % % % % % % % % % % % % %   方法1： 算术平均法求权重   % % % % % % % % % % % % %
  74.    % 第一步：将判断矩阵按照列归一化（每一个元素除以其所在列的和）
  75.     % 第二步：将归一化的各列相加
  76.     % 第三步：将相加后的向量除以n即可得到权重向量
  78.     Sum_A = sum(A);
  79.     % matlab中的sum函数的用法
  80.     % a=sum(x);%按列求和
  81.     % a=sum(x,2);%按行求和
  82.     % a=sum(x(:));%对整个矩阵求和
  84.     % % 基础：matlab中如何提取矩阵中指定位置的元素？
  85.     % % （1）取指定行和列的一个元素（输出的是一个值）
  86.     % %     A(2,1)  A(3,2)
  87.     % % （2）取指定的某一行的全部元素（输出的是一个行向量）
  88.     % %     A(2,:)  A(5,:)
  89.     % % （3）取指定的某一列的全部元素（输出的是一个列向量）
  90.     % %     A(:,1)  A(:,3)
  91.     % % （4）取指定的某些行的全部元素（输出的是一个矩阵）
  92.     % %    A([2,5],:)      只取第二行和第五行（一共2行）
  93.     % %    A(2:5,:)        取第二行到第五行（一共4行）
  94.     % % （5）取全部元素(按列拼接的，最终输出的是一个列向量)
  95.     % %    A(:)
  97.     SUM_A = repmat(Sum_A,n,1);
  98.     % B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。
  99.     % 另外一种替代的方法如下：
  100.     % SUM_A = [];
  101.     % for i = 1:n  %循环哦，不需要加冒号，这里表示循环n次
  102.     %     SUM_A = [SUM_A;Sum_A];
  103.     % end
  105.     Stand_A = A ./ SUM_A;
  106.     % MATLAB在矩阵的运算中，“*”号和“/”号代表矩阵之间的乘法与除法，对应元素之间的乘除法需要使用“./”和“.*”
  107.     % 这里我们直接将两个矩阵对应的元素相除即可
  109.     disp('算术平均法求权重的结果为：');
  110.     disp(sum(Stand_A,2) / n)
  111.     % 首先对标准化后的矩阵按照行求和，得到一个列向量，然后再将这个列向量的每个元素同时除以n即可（注意这里也可以用./哦）
  114.     % % % % % % % % % % % % %   方法2： 几何平均法求权重   % % % % % % % % % % % % %
  116.     % 第一步：将A的元素按照行相乘得到一个新的列向量
  117.     Prduct_A = prod(A,2);
  118.     % prod函数和sum函数类似，一个用于乘，一个用于加
  120.     % 第二步：将新的向量的每个分量开n次方
  121.     Prduct_n_A = Prduct_A .^ (1/n);
  122.     % 这里对元素操作，因此要加.号哦。  ^符号表示乘方哦  这里是开n次方，所以我们等价求1/n次方
  124.     % 第三步：对该列向量进行归一化即可得到权重向量
  125.     % 将这个列向量中的每一个元素除以这一个向量的和即可
  126.     disp('几何平均法求权重的结果为：');
  127.     disp(Prduct_n_A ./ sum(Prduct_n_A))
  130.     % % % % % % % % % % % % %   方法3： 特征值法求权重   % % % % % % % % % % % % %
  132.     % 计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法：
  133.     % （1）E=eig(A)：求矩阵A的全部特征值，构成向量E。
  134.     % （2）[V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。（V的每一列都是D中与之相同列的特征值的特征向量）
  135.     [V,D] = eig(A);    %V是特征向量, D是由特征值构成的对角矩阵（除了对角线元素外，其余位置元素全为0）
  136.     Max_eig = max(max(D)); %也可以写成max(D(:))哦~
  138.     % 那么怎么找到最大特征值所在的位置了？ 需要用到find函数，它可以用来返回向量或者矩阵中不为0的元素的位置索引。
  139.     % 下面例子来自博客：https://www.cnblogs.com/anzhiwu815/p/5907033.html
  140.     % 关于find函数的更加深入的用法可参考原文
  141.     % >> X = [1 0 4 -3 0 0 0 8 6];
  142.     % >> ind = find(X)
  143.     % ind =
  144.     %    1     3     4     8     9
  145.     % 其有多种用法，比如返回前2个不为0的元素的位置：
  146.     % >> ind = find(X,2)
  147.     % >> ind =
  148.     %     1     3
  149.     %若X是一个矩阵，索引该如何返回呢？
  150.     %  >> X = [1 -3 0;0 0 8;4 0 6]
  151.     %  X =
  152.     %   1    -3     0
  153.     %   0     0     8
  154.     %   4     0     6
  155.     %  >> ind = find(X)
  156.     % ind =
  157.     %      1
  158.     %      3
  159.     %      4
  160.     %      8
  161.     %      9
  162.     % 这是因为在Matlab在存储矩阵时，是一列一列存储的，我们可以做一下验证：
  163.     %  >> X(4)
  164.     %  ans =
  165.     %     -3
  166.     % 假如你需要按照行列的信息输出该怎么办呢？
  167.     % [r,c] = find(X)
  168.     % r =
  169.     %      1
  170.     %      3
  171.     %      1
  172.     %      2
  173.     %      3
  174.     % c =
  175.     %      1
  176.     %      1
  177.     %      2
  178.     %      3
  179.     %      3
  180.     % [r,c] = find(X,1) %只找第一个非0元素
  181.     % r =
  182.     %      1
  183.     % c =
  184.     %      1
  186.     % 那么问题来了，我们要得到最大特征值的位置，就需要将包含所有特征值的这个对角矩阵D中，不等于最大特征值的位置全变为0
  187.     % 这时候可以用到矩阵与常数的大小判断运算，共有三种运算符：大于> ;小于< ;等于 ==  （一个等号表示赋值；两个等号表示判断）
  188.     % 例如：A > 2 会生成一个和A相同大小的矩阵，矩阵元素要么为0，要么为1（A中每个元素和2比较，如果大于2则为1，否则为0）
  189.     [r,c]=find(D == Max_eig , 1);
  190.     % 找到D中第一个与最大特征值相等的元素的位置，记录它的行和列。
  192.     disp('特征值法求权重的结果为：');
  193.     disp( V(:,c) ./ sum(V(:,c)) )
  194.     % 我们先根据上面找到的最大特征值的列数c找到对应的特征向量，然后再进行标准化。
  197.     % % % % % % % % % % % % %  下面是计算一致性比例CR的环节  % % % % % % % % % % % % %
  199.     % 当CR<0.10时，我们认为判断矩阵的一致性可以接受；否则应对其进行修正。
  200.     CI = (Max_eig - n) / (n-1);
  201.     RI=[0 0.00001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
  202.     % 这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
  203.     CR=CI/RI(n);
  204.     disp('一致性指标CI=');disp(CI);
  205.     disp('一致性比例CR=');disp(CR);
  206.     if CR<0.10
  207.         disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
  208.     else
  209.         disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
  210.     end
  211. elseif ERROR == 1
  212.     disp('请检查矩阵A的维数是否不大于1或不是方阵')
  213. elseif ERROR == 2
  214.     disp('请检查矩阵A中有元素小于等于0')
  215. elseif ERROR == 3
  216.     disp('A的维数n超过了15，请减少准则层的数量')
  217. elseif ERROR == 4
  218.     disp('请检查矩阵A中存在i、j不满足A_ij * A_ji = 1')
  219. end
  221. % % 注意：代码文件仅供参考，一定不要直接用于自己的数模论文中
  222. % % 国赛对于论文的查重要求非常严格，代码雷同也算作抄袭

代码降重方法：

  1. 增加注释（甚至可以每一行都加注释）
  2. 替换变量名
  3. 增加恶心字符（emmmm…不作说明）
  4. 附录代码块变为图片

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HjW9JWi4-1657161871594)(D:\\软件\\Typora\\文件夹\\image-20220705152724644.png)\]

AHP的局限性

\[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RBwgNY66-1657161871595)(C:\\Users\\nzd\_mbl\\AppData\\Roaming\\Typora\\typora-user-images\\image-20220705152939907.png)\]

如果决策层中的指标数据是已知的，那可以选择TOPSIS法（优劣解距离法）

发表评论

表情：
评论列表 （有 0 条评论，227人围观）

还没有评论，来说两句吧...

相关阅读

    相关 层次分析法笔记

    层次分析法 什么时候用？ 层次分析法是将决策问题按目标层、决策层（可含多个决策层）、方案层的顺序分为不同的层次结构，然后用求解判断矩阵特征向量的办法，求得每一层次的各元素

    - 日理万妓- 日理万妓/ 0 赞/ 138 阅读

    相关 pandas实现层次分析法

    使用到了特征向量的和积法求出了数值解，避免了使用numpy自带函数产生复数解的缺点。因为在大部分情况下，决策者得到的判断矩阵都不是对称的，必然会运行出复数解。 算例使用的是

    左手的ㄟ右手左手的ㄟ右手/ 0 赞/ 316 阅读