B树、B+树、B*树-蒲公英云

B树、B+树、B*树

B树及其变种是数据库存储主要数据形式之一

二叉搜索树

在说明B树之前，先说明一下B树的基础——二叉搜索树

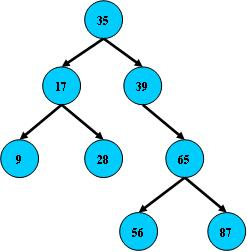
所有非叶子结点至多拥有两个儿子（Left 和 Right）；
所有结点存储一个关键字；
非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；
如图所示：

使用

二叉搜索树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；

优势

如果二叉搜索树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么 B 树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变二叉搜索树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；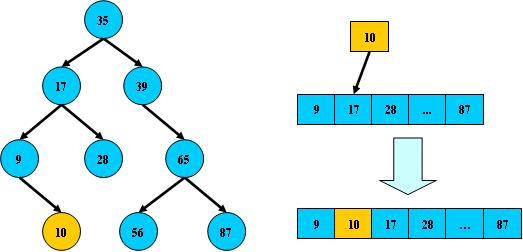
在这里插入图片描述

限制

二叉搜索树在经过多次插入与删除后，有可能导致线性结构：

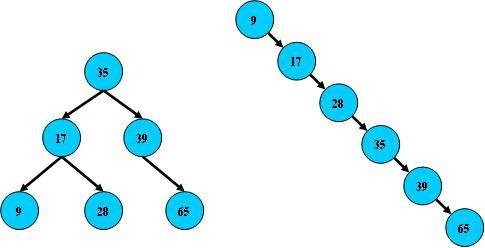
在这里插入图片描述

实际使用的二叉搜索树都是在原二叉搜索树的基础上加上平衡算法，即 “平衡二叉树” ，这就是B树，当然，在实际使用过程，树不仅仅限于二叉，通常都是多叉的

B树

定义任意非叶子结点最多只有 M 个儿子；且 M>2；
根结点的儿子数为 [2, M]；
除根结点以外的非叶子结点的儿子数为 [M/2, M]；
每个结点存放至少 M/2-1（取上整）和至多 M-1 个关键字；（至少 2 个关键字）
非叶子结点的关键字个数 = 指向儿子的指针个数 - 1；
非叶子结点的关键字：K [1], K [2], …, K [M-1]；且 K [i] < K [i+1]；
非叶子结点的指针：P [1], P [2], …, P [M]；其中 P [1] 指向关键字小于 K [1] 的子树，P [M] 指向关键字大于 K [M-1] 的子树，其它 P [i] 指向关键字属于 (K [i-1], K [i]) 的子树；
所有叶子结点位于同一层；

如：（M=3）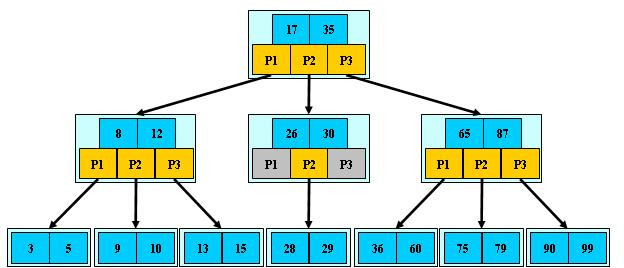
在这里插入图片描述

使用

B - 树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

特性：

关键字集合分布在整颗树中；
任何一个关键字出现且只出现在一个结点中；
搜索有可能在非叶子结点结束；
其搜索性能等价于在关键字全集内做一次二分查找；
自动层次控制；

B+树

B + 树是 B - 树的变体，也是一种多路搜索树：

其定义基本与 B - 树同，除了：
非叶子结点的子树指针与关键字个数相同；
非叶子结点的子树指针 P [i]，指向关键字值属于 [K [i], K [i+1]) 的子树，B - 树是开区间
为所有叶子结点增加一个链指针；
所有关键字都在叶子结点出现；

如：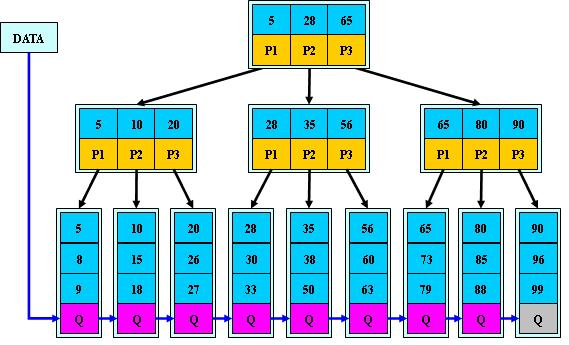
在这里插入图片描述

使用

B + 的搜索与 B - 树也基本相同，区别是 B + 树只有达到叶子结点才命中（B - 树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

特性

所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
不可能在非叶子结点命中；
非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
更适合文件索引系统；

B*树

是 B + 树的变体，在 B + 树的非根和非叶子结点再增加指向兄弟的指针；

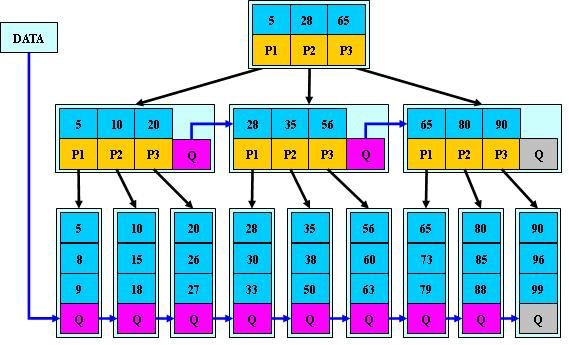
在这里插入图片描述

B * 树定义了非叶子结点关键字个数至少为 (2/3)*M，即块的最低使用率为 2/3（代替 B + 树的 1/2）；

B + 树的分裂：当一个结点满时，分配一个新的结点，并将原结点中 1/2 的数据复制到新结点，最后在父结点中增加新结点的指针；B + 树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B * 树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制 1/3 的数据到新结点，最后在父结点增加新结点的指针；

所以，B * 树分配新结点的概率比 B + 树要低，空间使用率更高；