动态规划凑硬币问题

Dear 丶 2021-10-01 11:34 333阅读 0赞

# 凑硬币问题 #

**假设有 1 元，3 元，5 元的硬币若干（无限），现在需要凑出 11 元，问如何组合才能使硬币的数量最少？**  
用数组d来存储当前每个面值可以对应的合成的最小数量  
d(i) = d(j) + 1  
这里 j < i。通俗地讲，我们需要凑出 i 元，就在凑出 j 的结果上再加上某一个硬币就行了。  
那这里加上的哪个硬币呢。把每个硬币试一下就行了：  
1.假设最后加上的是 1 元硬币，那 d(i) = d(j) + 1 = d(i - 1) + 1。  
2.假设最后加上的是 3 元硬币，那 d(i) = d(j) + 1 = d(i - 3) + 1。  
3.假设最后加上的是 5 元硬币，那 d(i) = d(j) + 1 = d(i - 5) + 1。  
我们分别计算出 d(i - 1) + 1，d(i - 3) + 1，d(i - 5) + 1 的值，取其中的最小值，即为最优解，也就是 d(i)。  
状态转移方程 d(i)=min\{d(j)+1\},if i>j  
d(0)=0;  
d(1)=1;  
d(2)=d(1)+1=2;  
d(3)=min\{d(2)+1,d(0)+1\}=1;  
d(4)=min\{d(3)+1,d(1)+1\}=2;  
d(5)=min\{d(4)+1,d(2)+1,d(0)+1\}=1;  
d(6)=min\{d(5)+1,d(3)+1,d(1)+1\}=2;

public class test1430 {
    
            private int[] d; // 储存结果
            private int[] coins = {1,3,5}; // 硬币种类
    
            private void d_func(int i, int num) {
                if (i == 0) {
                    d[i] = 0;
                    d_func(i + 1, num);
                }
                else {
                    int min = 1000000; // 初始化一个很大的数值。当最后如果得出的结果是这个数时，说明凑不出来。
                    for (int coin : coins) {
                        if (i >= coin && d[i - coin] + 1 < min) {//比较得到最小值
                            min = d[i - coin] + 1;
                        }
                    }
                    d[i] = min;
    
                    if (i < num) {
                        d_func(i + 1, num);
                    }
                }
            }
    
    
            @Test
            public void test() throws Exception {
                int sum = 11; // 需要凑 11 元
                d = new int[sum + 1]; // 初始化数组
    
                d_func(0, sum); // 计算需要凑出 0 ～ sum 元需要的硬币数量
                for (int i = 0; i <= sum; i++) {
                    System.out.println("凑齐 " + i + " 元需要 " + d[i] + " 个硬币");
                }
            }
    }

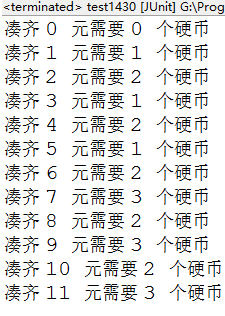
![5057999-e72e53dbeb5bcbd2.png][]

运行结果

当测试数据换成3、10、12.发现无法合成的数据也可以表示出来。因为其无法参与赋值，所以结果还是设置的Min=1000000

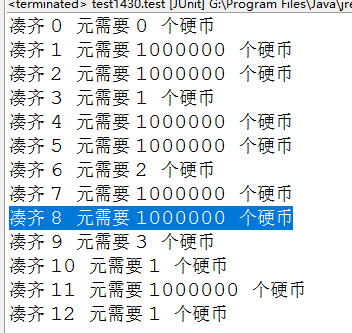
![5057999-42b16e14279f2265.png][]

### 思考：如果要求得需要的最大硬币数 应该如何处理 ###

这里花了我好久的时间 感觉自己真的是蠢 智商不够 想了一种方法 就是用t数组存最大数值，然后每次和max比较，将最大的留下。当然考虑到有的没办法获得，则没办法获得的赋值为0。结合前面的进行更改。写的不好，如果有好一点的方法希望能说一下。

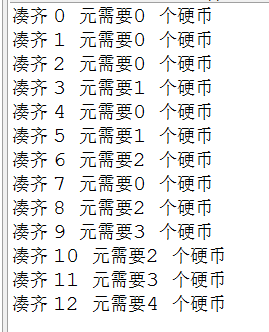
private static int[] d; // 储存结果
            private static int[] t;
            private static int[] coins = {3,5,6}; // 硬币种类
    
       private static void d_func_max(int i, int num) {
                if (i == 0) {
                    d[i] = 0;
                    t[i]=0;
                    d_func_max(i + 1, num);
                }
                else {
                    int min = 1000000; // 初始化一个很大的数值。当最后如果得出的结果是这个数时，说明凑不出来。
                    
                    for (int coin : coins) {
                        if (i >= coin && d[i - coin] + 1 < min) {
                            min = d[i - coin] + 1;
                        }
                    }
                    d[i] = min;
                    
                    int max=0;
                    for (int coin : coins) {
                        if(d[i]==1000000){
                            break;
                        }
                        if (i >= coin && t[i - coin] + 1 > max) {
                            max = t[i - coin] + 1;
                        }
                    }
                    t[i]=max;
                    
                    if (i < num) {
                        d_func_max(i + 1, num);
                    }
                }
            }
            
    
    
            
            public static void main(String[] args){
                int sum = 12; // 需要凑 11 元
                d = new int[sum + 1]; // 初始化数组
                t= new int[sum+1];
                d_func_max(0, sum); // 计算需要凑出 0 ～ sum 元需要的硬币数量
                for (int i = 0; i <= sum; i++) {
                    System.out.println("凑齐 " + i + " 元最多需要"+t[i] + " 个硬币");
                }
            }
    }

测试数据3、5、6。结果如图

![5057999-c9972396b339bd4f.png][]

[5057999-e72e53dbeb5bcbd2.png]: /images/20210811/1d17b88d02254aa397328c7ca8f50204.png
[5057999-42b16e14279f2265.png]: /images/20210811/bb618332cb8740b2aee2c5689e597a38.png
[5057999-c9972396b339bd4f.png]: /images/20210811/9e7589faa35e462f8666e2f06691e2b9.png