无向图的动态规划——硬币问题-蒲公英云

无向图的动态规划——硬币问题

以你之姓@ 2022-05-08 12:36 338阅读 0赞

题目描述：
硬币找零问题描述：现存在一堆面值为 V1、V2、V3 … 个单位的硬币
问最多和最少需要多少个硬币才能找出总值为T个单位的零钱？
输入：
第一行为n，T，表示硬币个数，需要凑的面额，第二行有n个数，表示硬币的面额
输出：
一行，分别为最大最小的数目，用空格分开
示例：
输入 5 63
1、2、5、21、25
输出 63 3
解题思路：
运用动态规划，将 Max【T】和Min【T】用来存储总面额为T时所需要的最多和最少
的硬币，Max【T】=max{Max【T-Vi】+1，Max【T】}，Min【T】=min{Min【T-vi】+1，
Min【T】}，将min【Vi】初始化为1，将max【vi】初始化为1

-—————————— 作者：braveryCHR 来源：CSDN 原文：https://blog.csdn.net/bravery\_again/article/details/72458067?utm\_source=copy

贪心解决：

关于最少硬币的数目，可以用贪心算法——每次选尽可能大的硬币，直至满足条件。

证明：见参考文章

代码：

#include<iostream>
#include<vector>
#include<stack>
#include<algorithm>
using namespace std;
const int maxnum=100;
int find_less(vector<int> &type,stack<int> &money,int s)
{
    int sum=0,bakesum;
    int len=type.size();
    int i;
    for(i=len-1;i>=0;i--)
    {
        while(sum<s)
        {
            sum+=type[i];
            money.push(type[i]);
            if(sum==s)
                return 1;
        }
        sum-=type[i];
        money.pop();
    }
    return 0;
}
int main()
{
    vector<int> type;//存钱的种类 
    stack<int> money;//存已经放入的钱
    int i,n,s;//用于记数，钱的种类数，总金额
    int tmp;
    //输入 
    cin>>n; 
    for(i=0;i<n;i++)
    {
        cin>>tmp;
        type.push_back(tmp);
    }
    cin>>s;
    sort(type.begin(),type.end());//将面额从小到大排序
    if(find_less(type,money,s))
    {
        while(!money.empty())
        {
            tmp=money.top();
            cout<<tmp<<" ";
            money.pop();
        }
    }
    else
        cout<<"no way";
    return 0;
}

动态规划——图：

开始的时候，怎么也想不出来咋可以用图来解决。后来想通了（如下图所示）。

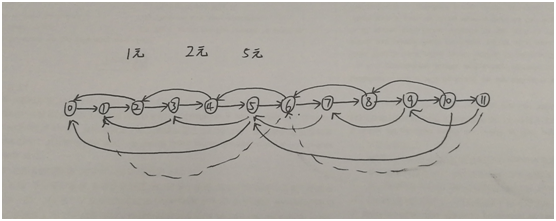
用递归的方式：

#include<iostream>
#include<vector>
#include<algorithm>
#include<climits>
using namespace std;
const int INF=10000;
const int maxmoney=100;
int Max[maxmoney];
int Min[maxmoney];
vector<int> type;
int n;
int minnum(int s)
{
    if(Min[s]!=-1)
        return Min[s];
    Min[s]=INF;
    for(int i=0; i<n; i++)
        if(s>=type[i])
            Min[s]=min(Min[s],minnum(s-type[i])+1);
    return Min[s];
}
int maxnum(int s)
{
    if(Max[s]!=-1)
        return Min[s];
    Max[s]=-INF;
    for(int i=0; i<n; i++)
        if(s>=type[i])
            Max[s]=max(Max[s],maxnum(s-type[i])+1);
    return Max[s];
}
int main()
{
    int i,m;
    cin>>n>>m;//n表示零钱的种类，m表示总金额
    int tmp;
    for(i=0;i<n;i++)
    {
        cin>>tmp;
        type.push_back(tmp);
    }
    sort(type.begin(),type.end());
    Max[0]=0;Min[0]=0;
    for(i=1;i<=m;i++)
    {
        Max[i]=-1;
        Min[i]=-1;
    }
    cout<<minnum(m)<<" "<<maxnum(m);
}

用递推的方式：

#include<iostream>
#include<vector>
#include<algorithm>
#include<climits>
using namespace std;
const int INF=10000;
const int maxmoney=100;
int Max[maxmoney];
int Min[maxmoney];
int main()
{
    int i,n,m;
    vector<int> type;
    cin>>n>>m;//n表示零钱的种类，m表示总金额 
    int tmp;
    for(i=0;i<n;i++)
    {
        cin>>tmp;
        type.push_back(tmp);
    }
    sort(type.begin(),type.end());
    Max[0]=0;Min[0]=0;
    for (int i=1;i<=m;++i)
    {
        Min[i]=INF;  //初始化为最大 
        Max[i]=-INF; //初始化为最小 
    }
    int t;
    for(t=1;t<=m;t++)
    {
        for(i=0;i<n;i++)
            if(t>=type[i])
            {
                Max[t]=max(Max[t],Max[t-type[i]]+1);
                Min[t]=min(Min[t],Min[t-type[i]]+1);
            }
    }
    cout<<Max[m]<<" "<<Min[m]<<endl;
    return 0;
}