877. 石子游戏 and 174. 地下城游戏-蒲公英云

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。每回合，玩家从行的开始或结束处取走整堆石头。这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

分析：由于题目的限制条件是石头的堆数是偶数，且石头的总数是奇数，因此Alex可以选择一种策略总是选偶数堆或者奇数堆的石头，则一定可以胜过Lee。简单说，Alex在题目的条件限制下是必胜的。但这里我们需要进行更一般化的分析，例如石头堆数不一定是偶数，石头总数也不一定是奇数，且不但要判断Alex是否能赢，还要判断最多赢多少分，如果输，能不能提供最少输多少分。这里的分数是指多拿的石头数量。

我们每次只能拿两端的石头堆的石头，但我们又不知道拿完后剩下的石头堆的情况，因此我们考虑先解决子问题。例如我们求出2个相邻石头堆的胜负情况，我们可以根据求出的数据求出相邻3个石头堆的胜负情况，以此类推，我们可以根据n-1个相邻石头堆的胜负情况，求出n个相邻石头堆的胜负情况，即我们的原问题。
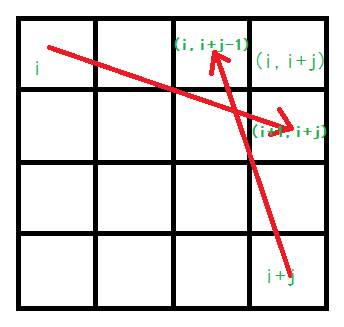
根据我们的类推我们可以设dp[i][j]为piles[i]~piles[j]Alex最多可以赢Lee的分数。每次取石头堆只能从两端取，因此:dp[i][j] = max(piles[i] - dp[i+1][j], piles[j] - dp[i][j-1])。其中
piles[i] - dp[i+1][j]表示Alex取走i上的石头堆，piles[j] - dp[i][j-1]表示Alex取走的是j上的石头堆。注意，为什么dp[i+1][j]表示piles[i+1]~piles[j]之间Alex最多可以赢Lee的分数，而piles[i]要减去该值而不是加上该值呢？由于我们的要求是每一步Alex和Lee采取的都是最优策略，当取piles[i]时，piles[i+1]~piles[j]中Alex和Lee的走法会调换。意即Lee走Alex的走法，Alex走Lee的走法，因此这里要做减法。

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MTMxODQwNQ_size_16_color_FFFFFF_t_70

public boolean stoneGame(int[] piles) {
        // dp其实就是存储了递归过程中的数值
        // dps[i][j]代表从i到j所能获得的最大的绝对分数
        // （比如为1就说明亚历克斯从i到j可以赢李1分）
        // 如何计算dps[i][j]呢:max(piles[i]-dp[i+1][j],piles[j]-dp[i][j-1]);
        // 这里减去dps数组是因为李也要找到最大的
        int n = piles.length;
        int[][] dps = new int[n][n];
        // dps[i][i]存储当前i的石子数
        for (int i = 0; i < n; i++)
            dps[i][i] = piles[i];
        // d=1,其实代表，先算两个子的时候
        // 此处为自己推导的执行流程，和正确答案一样！！！！！！！！！！！！！！！！！！！！！！
        for (int i = n - 1; i >= 0; i--) {
            for (int j = i + 1; j < n; j++) {
                dps[i][j] = Math.max(piles[i] - dps[i + 1][j], piles[j] - dps[i][j - 1]);
            }
        }
//        for (int d = 1; d < n; d++) {
//            // 有多少组要比较
//            for (int j = 0; j < n - d; j++) {
//                // 比较j到d+j
//                dps[j][d + j] = Math.max(piles[j] - dps[j + 1][d + j], piles[d + j] - dps[j][d + j - 1]);
//            }
//        }
        return dps[0][n - 1] > 0;
}

一些恶魔抓住了公主（P）并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士（K）最初被安置在左上角的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快到达公主，骑士决定每次只向右或向下移动一步。

编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。

例如，考虑到如下布局的地下城，如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下，则骑士的初始健康点数至少为 7。

分析：由于题目不知道左上角（刚开始）的健康点数，所以想到可以逆着推，从右下角往回推。dp[i][j]表示在进入（i，j）格子的初始时刻所应拥有的最小生命值。比如右下角的格子值为-5，则dp[m-1][n-1]应该等于6. 考虑一般状态，因为只能向下或向右行走，所以若知道在进入下面或右面的格子初始时刻所需要的最小生命值，只要用两者之间最小值减去当前格子内的值，即可得到进入当前格子初始时刻所应拥有的最小生命值。需要注意，若计算得到的结果小于等于零，则必须将结果设为1，因为一旦生命值小于1就会死亡。得到递推关系式：dp[i][j]=max(1, min(dp[i][j+1] , dp[i][j+1]) - dungeon[i][j] ); 另外需要特殊处理右边界和下边界：

public int calculateMinimumHP(int[][] dungeon) {
        int M = dungeon.length;
        if(M == 0)
            return 0;
        int N = dungeon[0].length;
        if(N == 0)
            return 0;
        int[][] dp =  new int[M][N];
        dp[M-1][N-1] = Math.max(1, 1-dungeon[M-1][N-1]);
        for(int i=N-2; i>=0; i--) {
            dp[M-1][i] = Math.max(1 , dp[M-1][i+1]-dungeon[M-1][i]);
        }
        for(int i=M-2; i>=0; i--) {
            dp[i][N-1] = Math.max(1 , dp[i+1][N-1]-dungeon[i][N-1]);
        }
        for(int i=M-2; i>=0; i--) {
            for(int j=N-2; j>=0; j--) {
                dp[i][j] = Math.max(1 , Math.min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]);
            }
        }
        return dp[0][0];
    }