leetcode 174. Dungeon Game | 174. 地下城游戏（暴力递归-＞傻缓存-＞dp）-蒲公英云

leetcode 174. Dungeon Game | 174. 地下城游戏（暴力递归-＞傻缓存-＞dp）

男娘i 2022-09-14 09:07 199阅读 0赞

题目

https://leetcode.com/problems/dungeon-game/
在这里插入图片描述

题解

方法1：4个参数的递归+缓存，TLE

今日结论：转换成dp之前，递归的参数设计很重要，参数越少越好

我第一版递归有4个参数，心想，加个缓存吧，当我写出4个map嵌套的时候，内心是绝望的。。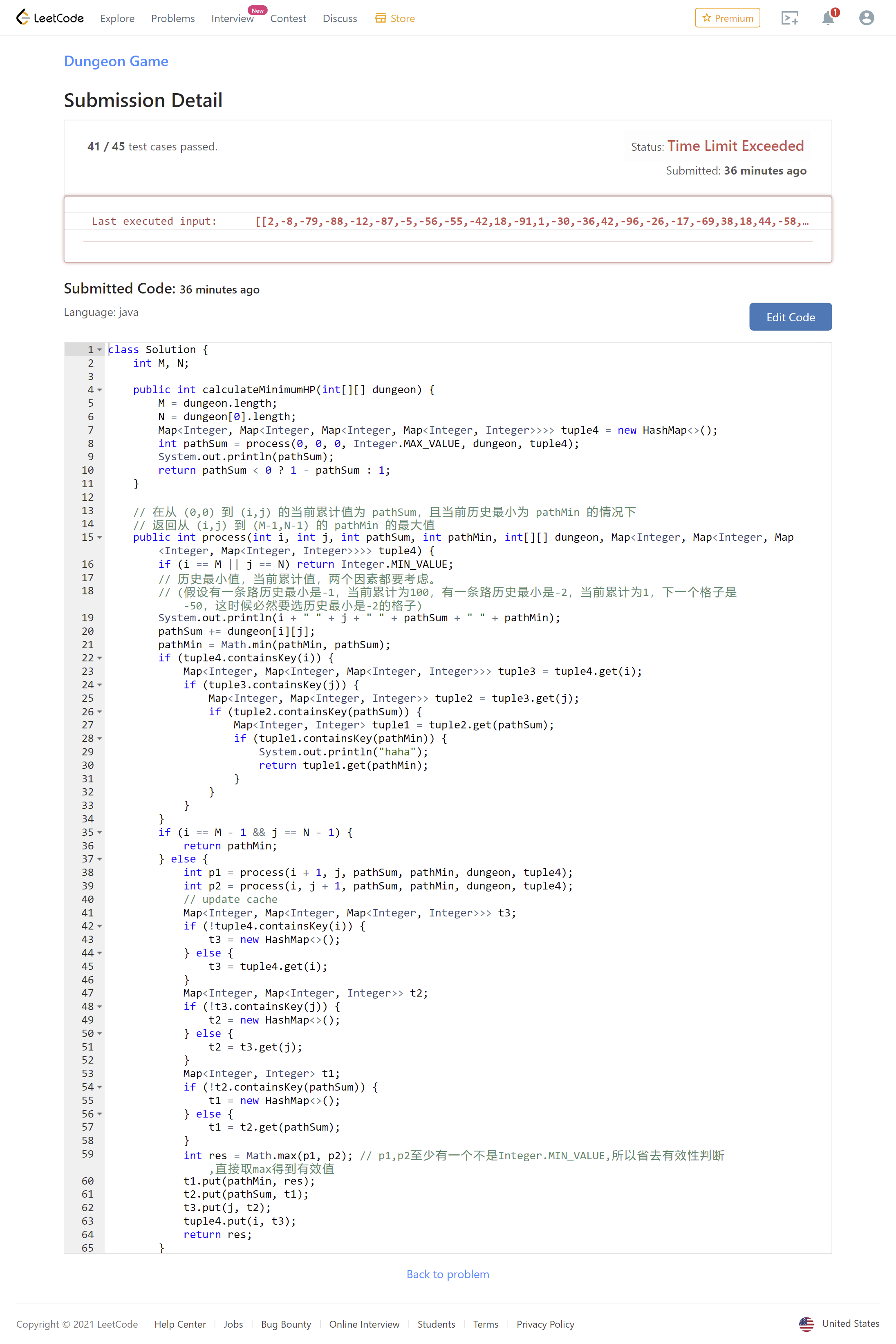
在这里插入图片描述

方法2：两个参数的dp

方法 1 超时，于是看了答案的递归版本：
https://leetcode.com/problems/dungeon-game/discuss/745340/post-Dedicated-to-beginners-of-DP-or-have-no-clue-how-to-start

然后用暴力递归->傻缓存->dp 的套路，转化成的自底向上的 dp。

class Solution { 
    int M, N;
    public int calculateMinimumHP(int[][] dungeon) { 
        M = dungeon.length;
        N = dungeon[0].length;
        int[][] dp = new int[M + 1][N + 1];
        // 【Solution 1】傻缓存
       // return process(0, 0, dungeon, dp);
        // 【Solution 2】dp
        for (int i = 0; i <= M; i++) { 
            dp[i][N] = Integer.MAX_VALUE;
        }
        for (int i = 0; i <= N; i++) { 
            dp[M][i] = Integer.MAX_VALUE;
        }
        dp[M - 1][N - 1] = dungeon[M - 1][N - 1] > 0 ? 1 : 1 - dungeon[M - 1][N - 1];
        for (int i = M - 1; i >= 0; i--) { 
            for (int j = N - 1; j >= 0; j--) { 
                if (i == M - 1 && j == N - 1) continue;
                int p1 = dp[i + 1][j];
                int p2 = dp[i][j + 1];
                int minReq = Math.min(p1, p2) - dungeon[i][j];
                dp[i][j] = minReq <= 0 ? 1 : minReq;
            }
        }
        return dp[0][0];
    }
    // return min requirement
    // public int process(int i, int j, int[][] dungeon, int[][] dp) { 
    // if (i == M || j == N) return Integer.MAX_VALUE;
    // if (dp[i][j] != 0) return dp[i][j];
    // if (i == M - 1 && j == N - 1) { 
    // return dungeon[i][j] > 0 ? 1 : 1 - dungeon[i][j];
    // } else { 
    // int p1 = process(i + 1, j, dungeon, dp);
    // int p2 = process(i, j + 1, dungeon, dp);
    // int minReq = Math.min(p1, p2) - dungeon[i][j];
    // dp[i][j] = minReq <= 0 ? 1 : minReq;
    // return dp[i][j];
    // }
    // }
}