动态规划
算法题中动态规划是真的难,写一篇总结,彻底解决动态规划。参考:https://blog.csdn.net/u013309870/article/details/75193592#commentsedit
核心:记住已经解决过的子问题。
A * "1+1+1+1+1+1+1+1 =?" *A : "上面等式的值是多少"B : *计算* "8!"A *在上面等式的左边写上 "1+" *A : "此时等式的值为多少"B : *quickly* "9!"A : "你怎么这么快就知道答案了"A : "只要在8的基础上加1就行了"A : "所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"
动态规划有两种方式(自顶向下和自底向上)以斐波那契为例。
自顶向下:
//自顶向下public static int Fibonacci(int n){if(n<=0)return n;int []Memo=new int[n+1];for(int i=0;i<=n;i++)Memo[i]=-1;return fib(n, Memo);}public static int fib(int n,int []Memo){if(Memo[n]!=-1)return Memo[n];//如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中。if(n<=2)Memo[n]=1;else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);return Memo[n];}
自底向上:
public static int feibo(int n){if(n<=0){return n;}int[] temp=new int[n+1];temp[0]=0;temp[1]=1;for(int i=2;i<=n;i++) {temp[i] = temp[i - 1] + temp[i - 2];}return temp[n];}
例题: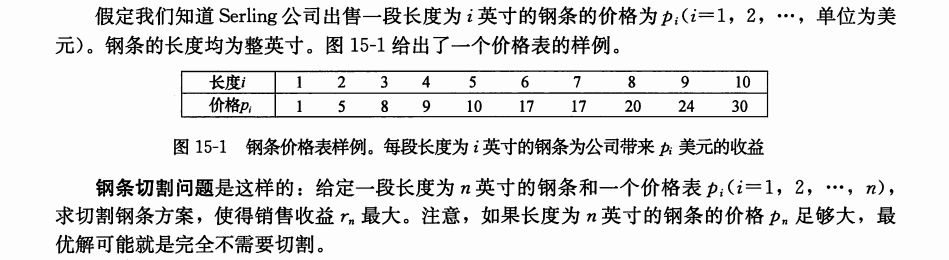





























还没有评论,来说两句吧...