动态规划-蒲公英云

动态规划

短命女 2022-05-17 09:45 443阅读 0赞

等我有时间了，一定要把《算法导论》啃完，这本书的印刷质量实在太好了，就是烧脑子，滑稽。

适合应用动态规划求解的最优化问题应该具备两个要素：

最优子结构：一个问题的最优解包含其子问题的最优解；

子问题重叠：子问题的空间足够小，问题的递归算法会反复求解相同的子问题，而不是一直生成新的子问题。

常见的可以用动态规划解决的问题有：

① 0-1背包问题

② 最长公共子序列

③ 最短路径

④ 最优二叉搜索树

① 0-1背包问题

问题描述：给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi 。问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

思路分析：动态规划的出发点就是要把问题分解为子问题，并找到子问题之间的递推关系式。

对于背包问题，一个物品要么放进包里要么不放进包里，就是说对于第i 个物品，能不能放进包里。第i 个物品能放进去的时候，是放进去收益大还是把空间流出来收益大。根据这个分割，可以找到这个背包对前i 种物品的解与对前i-1 种物品的解之间的关系。

Java实现如下

public static int DP01(int[] weight, int[] value, int capcity) {
        int[][] best = new int[value.length+1][capcity+1];
        for(int i=0;i<value.length+1;i++) best[i][0]=0;
        for(int i=0;i<capcity+1;i++) best[0][i]=0;
        for(int i=1;i<value.length+1;i++){
            for(int j=1;j<capcity+1;j++){
                if(weight[i-1]>j){
                    best[i][j] = best[i-1][j];
                }else{
                    best[i][j] = Math.max(value[i-1]+best[i-1][j-weight[i-1]], best[i-1][j]);
                }
            }
        }
        return best[value.length][capcity];
    }

② 最长公共子序列（LCS）

问题描述：设两个序列X={x1,x2,…,xm}，Y={y1,y2,…,yn}，求XY的最长公共子序列。

思路分析：这个问题的分解的入手点是看xm是不是等于yn，而问题规模大小来自两个序列的长度。

若xm=yn，那么Xm 与Yn 的LCS 为Xm-1 与Yn-1 的LCS + xm，长度为后者的长度+1；

若xm!=yn，那么 Xm 与Yn 的LCS 为Xm-1 与Yn 的LCS 或者Xm 与Yn-1 的LCS，从这两者中选出较长的一个，我们定义c[i,j] 为Xi 和Yj 的LCS 长度，即Xm 的前 i 项和Yn 的前 j 项的LCS长度，得到一个递推的关系式。

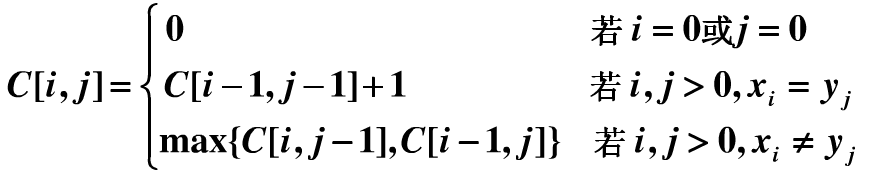
分析的时候自顶向下，发现求解过程是递归的，但用递归求解的话因为子问题的重叠，会导致重复计算，增加时间复杂度（因为i,j 的取值，会导致重复计算c[i-1,j-1]、c[i,j-1]、c[i-1,j]），所以在求解的时候采用自底向上循环求解，也就是动态规划。

Java实现如下

public static int LCS(char[] x, char[] y) {
        int[][] lcs  = new int[x.length+1][y.length+1];
        int[][] direction = new int[x.length+1][y.length+1];//1-左上角，2-上面，3左边
        lcs[0][0] = 0;
        lcs[0][1] = 0;
        lcs[1][0] = 0;
        for(int i=1;i<=x.length;i++){
            for(int j=1;j<=y.length;j++){
                if(x[i-1]==y[j-1]){
                    lcs[i][j] = lcs[i-1][j-1]+1;
                    direction[i][j] = 1;
                }else if(lcs[i-1][j]> lcs[i][j-1]){
                    lcs[i][j] = lcs[i-1][j];
                    direction[i][j] = 2;
                }else{
                    lcs[i][j] = lcs[i][j-1];
                    direction[i][j] = 3;
                }
            }
        }
        StringBuilder result = new StringBuilder();
        for(int i=x.length,j=y.length;i>0&&j>0;){//沿着路径往回找
            switch(direction[i][j]){
                case 1:
                result.append(x[i-1]);//相同的字符
                i--;
                j--;
                break;
                case 2:
                i--;break;
                case 3:
                j--;break;
                default:
                break;
            }
        }
        System.out.println(result.reverse());
        return lcs[x.length][y.length];
    }