递推(二):递推法的应用
下面通过一些典型实例及其扩展来讨论递推法的应用。
【例2】骨牌铺方格
在2×n的一个长方形方格中,用一种2×1的骨牌铺满方格。输入n(n<=40),输出铺放方案的总数。例如n=3时,为2×3方格,骨牌的铺放方案有三种,如下图1所示。
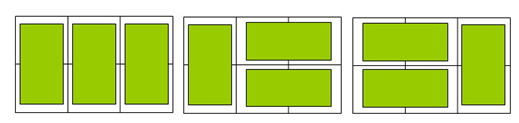
图1 2×3方格的骨牌铺放方案
(1)编程思路。设f\[i\]为铺满2\*n方格的方案数,则有 f\[i\]=f\[i-1\]+f\[i-2\]。其中,f\[i-1\]为铺满2\*(n-1)方格的方案数(既然前面的2\*(n-1)的方格已经铺满,那么最后一个只能是竖着放)。f\[i-2\]为铺满2\*(n-2)方格的方案数(如果前面的2\*(n-2)的方格已经铺满,那么最后的只能是横着放两块,否则会重复)。初始情况为:f\[1\]=1,f\[2\]=2。(2)源程序。
#include
using namespace std;
int main()
{
int i,n,f\[41\];cin>>n;f\[1\]=1;f\[2\]=2;for(i=3;i<=n;i++)f\[i\]=f\[i-1\]+f\[i-2\]; // 按递推关系实施递推cout<<f\[n\]<<endl;return 0;
}
(3)问题扩展。有一个大小是2×n的长方形方格,现用2种规格的骨牌铺满,骨牌规格分别是 2×1和2×2。输入n(n<=30),输出铺放方案的总数。(4)扩展问题编程思路。铺方格的骨牌规格多了一种,递推公式做相应变化。设f\[i\]为铺满2\*n方格的方案数,则有 f\[i\]=f\[i-1\]+2\*f\[i-2\]。其中,f\[i-1\]为铺满2\*(n-1)方格的方案数(既然前面的2\*(n-1)的方格已经铺满,那么最后一个只能是竖着放)。f\[i-2\]为铺满2\*(n-2)方格的方案数(如果前面的2\*(n-2)的方格已经铺满,那么最后的2\*2方格或者横着放两块2\*1的骨牌,或者放1块2\*2的骨牌)。初始情况为:f\[1\]=1,f\[2\]=3。(5)扩展问题的源程序。
#include
using namespace std;
int main()
{
int i,n,f\[31\];cin>>n;f\[1\]=1;f\[2\]=3;for(i=3;i<=n;i++)f\[i\]=f\[i-1\]+2\*f\[i-2\]; // 按递推关系实施递推cout<<f\[n\]<<endl;return 0;
}
【例3】上台阶
设有一个共有n级的台阶,某人上台阶一步可上1级,也可上2级。编写一个程序,输入台阶的级数n(n<=40),输出某人从底层上到台阶顶层的走法的种数。(1)编程思路。先考虑最简单的情况。如果只有1级台阶,那显然只有一种上法。如果有2级台阶,那就有两种上的方法了:一种是分两次上,每次上1级;另外一种就是一次上2级。再来讨论一般情况。设把n级台阶时的上法看成是n的函数,记为f(n)。当n>2时,第一次上的时候就有两种不同的选择:一是第一次只上1级,此时上法数目等于后面剩下的n-1级台阶的上法数目,即为f(n-1);另外一种选择是第一次上2级,此时上法数目等于后面剩下的n-2级台阶的上法数目,即为f(n-2)。因此n级台阶时的不同上法的总数f(n)=f(n-1)+(f-2)。由此推导出递推公式 f(n)=f(n-1)+(f-2) (n>2)初始情况:f(1)=1; f(2)=2。(2)源程序。
#include
using namespace std;
int main()
{
int k,n,f\[41\];cout<<"请输入台阶总数n:";cin>>n;f\[1\]=1;f\[2\]=2;for(k=3;k<=n;k++)f\[k\]=f\[k-1\]+f\[k-2\]; // 按递推关系实施递推cout<<"上法总数为 "<<f\[n\]<<endl;return 0;
}
(3)扩展1。设一个台阶有n级,一步有m种跨法,一步跨多少级均从键盘输入(输入的级数从小到大)。求从底层上到台阶顶层的走法的种数。(4)扩展1的编程思路。例如,设有10级台阶,输入的m依次为2、4、7。递推式可写成f(n)=f(n-2)+f(n-4)+f(n-7) (n>=8)。但由于事先不知输入的是2、4、7,所以递推初始情况f(1)~f(7)无法直接赋初值,也就无法用一个这个单纯的递推式直接递推。必须先采用某种方法根据输入的m个一步上的台阶数将初始条件求取出来。实际上,可以将上台阶的递推分成多级递推,这样初始条件可在分级递推中求取。
当第1次输入2时,f(1)=0,f(2)=1。(初始条件)
当第2次输入4时,第1级递推:
f(3)=f(3-2)=0, f(4)=f(4-2)+1=2。(因为4本身即为一个一步到位的上法)
当第3次输入7时,第2级递推:
f(5)=f(5-2)+f(5-4)=0,f(6)=f(6-2)+f(6-4)=3,f(7)=f(7-2)+f(7-4)+1=1。
为求第10级台阶上法,采用三级递推:
f(8)=f(8-2)+f(8-4)+f(8-7)=5,f(9)=f(9-2)+f(9-4)+f(9-7)=2,
f(10)=f(10-2)+f(10-4)+f(10-7)=8。
下面探讨一般情况。
设上n级台阶的不同上法为f(n),从键盘输入一步跨多少级的m个整数分别为x(1)、x(2)、…、x(m),输入时约定1<=x(1) <x(2) <…<x(m)。
当1<=n<x(1) 时,f(n)=0; f(x(1))=1。(初始条件)
当x(1)<n<x(2) 时,第1级递推:f(n)=f(n−x(1));
f(x(2))=f(n-x(1))+1 (存在x2这个一步到位的上法)。
当x(2)<n<x(3) 时,第2级递推:f(n)=f(n−x(1))+f(n−x(2));
f(x(3))=f(n-x(1))+ f(n−x(2)) +1 (存在x3这个一步到位的上法)。
……
当x(m-1)<n<x(m),有第m-1级递推:f(n)=f(n−x(1))+f(n−x(2))+…+f(n−x(m-1));
f(x(m))=f(n−x(1))+f(n−x(2))+…+f(n-x(m-1))+1。
当x(m)<n时,第m级递推: f(n)=f(n−x(1))+f(n−x(2))+…+f(n−x(m))
为了便于统一处理,不妨附设一个x(m+1),使得x(m+1)=max(x(m),n)+1。
这样第m级递推统一描述为:
当x(m)<n<x(m+1) 时,第m级递推: f(n)=f(n−x(1))+f(n−x(2))+…+f(n−x(m))f(x(m+1))= f(n−x(1))+f(n−x(2))+…+f(n−x(m))+1。(5)扩展1的源程序。
#include
using namespace std;
int main()
{
int i,j,k,m,n,t,x\[10\],f\[51\];cout<<"请输入总台阶数:";cin>>n;cout<<"一次有几种跳法:";cin>>m;cout<<"请从小到大输入一步跳几级。"<<endl;for(i=1; i<=m; i++)cin>>x\[i\];for(i=1;i<x\[1\];i++) f\[i\]=0;f\[x\[1\]\]=1;x\[m+1\]=(x\[m\]>n?x\[m\]:n)+1;for(k=1;k<=m;k++)for(t=x\[k\]+1;t<=x\[k+1\];t++)\{f\[t\]=0;for(j=1;j<=k;j++) // 按公式累加实现分级递推f\[t\]=f\[t\]+f\[t-x\[j\]\];if(t==x\[k+1\])f\[t\]=f\[t\]+1;\}cout<<"共有不同的跳法种数为 "<<f\[n\]<<endl;return 0;
}
(6)扩展2。例3中的递推式实际上就是斐波那契数列的递推式。这个数列的增长很快,46项以后就会超过整型数据的表数范围。现设台阶有1000级,按一步可上1级,也可上2级的上法,不同的上法种数是一个209位的整数,如何正确求得这个种数。(7)扩展2的编程思路。由于要求的数据超过了整数表示的范围,需要进行高精度计算。如何表示和存放大数呢?一个简单的方法就是:用数组存放和表示大数。一个数组元素,存放大数中的一位。我们日常书写一个大整数,左侧为其高位,右侧为其低位,在计算中往往会因进位(carry)或借位(borrow)导致高位增长或减少,因此可以定义一个整型数组(int bignum\[maxlen\])从低位向高位实现大整数的存储,数组的每个元素存储大整数中的一位。显然,在C++中,int类型(4个字节/32位计算机)数组元素存储十进制的一位数字非常浪费空间,并且运算量也非常大,因此可将存储优化为万进制,即数组的每个元素存储大整数数字的四位。(为什么选择万进制,而不选择更大的进制呢?这是因为万进制中的最大值9999相乘时得到的值是99980001,不会超过4个字节的存储范围,而十万进制中的最大值99999相乘时得到的值是9999800001,超过4个字节的存储范围而溢出,从而导致程序计算错误。)在编写程序代码过程中作如下定义:
const int base=10000;
const int maxlen=50+1;
int bignum[maxlen];
说明:base表示进制为万进制,maxlen表示大整数的长度,1个元素能存储4个十进制位,50个元素就存储200个十进制位,而加1表示下标为0的元素另有它用,程序用作存储当前大整数的位数。下面讨论大整数的加法运算的实现。可以采用小学中曾学习的竖式加法。两个大整数98240567043826400046和3079472005483080794进行加法运算,如图2所示。
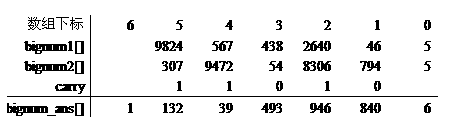
图2 加法的计算过程
从图2中可以得知,做加法运算是从低位向高位进行,如果有进位,下一位进行相加时要加上进位,如果最高位已计算完还有进位,就要增加存储结果的位数,保存起进位来。关于进位的处理,一般定义单独变量carry进行存储。(8)扩展2的源程序。
#include
using namespace std;
const int base=10000;
const int maxlen=60+1;
void addition(int *bignum1, int *bignum2, int *bignum_ans);
void printbignum(int *bignum);
int main()
{
int k,n,f\[1001\]\[maxlen\];cout<<"请输入台阶总数n:";cin>>n;f\[1\]\[0\]=1; f\[1\]\[1\]=1;f\[2\]\[0\]=1; f\[2\]\[1\]=2;for(k=3;k<=n;k++)addition(f\[k-1\],f\[k-2\],f\[k\]); // 按递推关系实施递推cout<<"上法总数为 ";printbignum(f\[n\]);return 0;
}
void addition(int *bignum1, int *bignum2, int *bignum_ans)
{
int carry=0;memset(bignum\_ans,0,sizeof(int)\*maxlen);bignum\_ans\[0\]=bignum1\[0\]>bignum2\[0\]?bignum1\[0\]:bignum2\[0\];for(int pos=1; pos<=bignum\_ans\[0\]; pos++)\{carry+=bignum1\[pos\]+bignum2\[pos\];bignum\_ans\[pos\]=carry%base;carry/=base;\}if(carry)bignum\_ans\[++bignum\_ans\[0\]\]=carry;
}
void printbignum(int *bignum)
{
int \*p=\*bignum+bignum;cout<<\*p--;cout.fill('0'); // 定义填充字符'0'while(p>bignum)\{ cout.width(4); cout<<\*p--; \}cout<<endl;
}
如果要求2000级台阶的不同上法种数(是一个418位的整数),上面的程序如何修改?如果求5000级甚至10000级的台阶呢?请读者自己动手做一做。在修改过程中,定义的二维数组造成栈溢出怎么办?(9)扩展3——第39级台阶。小明刚刚看完电影《第39级台阶》,离开电影院的时候,他数了数礼堂前的台阶数,恰好是39级! 站在台阶前,他突然又想着一个问题:如果我每一步只能迈上1个或2个台阶。先迈左脚,然后左右交替,最后一步是迈右脚,也就是说一共要走偶数步。那么,上完39级台阶,有多少种不同的上法呢?(10)扩展3的编程思路。由于在上台阶的过程中需要考虑不同的迈脚情况,因此需要定义二维数组c\[40\]\[2\],数组元素c\[i\]\[0\]表示上到第i级台阶时最后一步是左脚的方法数,c\[i\]\[1\] 表示上到第i级台阶时最后一步是右脚的方法数。
由于每一步能上一级或两级台阶,因此可得递推式:
c[i][0] = c[i-1][1]+c[i-2][1] (因为最后一步为左脚,倒数第二步肯定为右脚)
c[i][1] = c[i-1][0]+c[i-2][0] (因为最后一步为右脚,倒数第二步肯定为左脚)
初始情况为:
c[1][0]=1,第一步左脚直接迈一级台阶。
c[1][1]=0,因为先迈左脚,右脚不可能落在第1级台阶。
c[2][0]=1,第一步左脚直接迈两级台阶。
c[2][1]=1,左右脚各迈一级台阶,右脚正好落在第2级台阶。
(11)扩展3的源程序。
#include
using namespace std;
int main()
{
int i;int c\[40\]\[2\];c\[1\]\[1\] = 0; c\[1\]\[0\]=1;c\[2\]\[1\] = 1; c\[2\]\[0\]=1;for(i = 3; i <= 39; ++i)\{c\[i\]\[0\] = c\[i - 1\]\[1\] + c\[i - 2\]\[1\];c\[i\]\[1\] = c\[i - 1\]\[0\] + c\[i - 2\]\[0\];\}cout<<c\[39\]\[1\]<<endl;return 0;
}
例2和例3采用的都是顺推,下面看一个采用倒推求解的实例。【例4】猴子吃桃有一个猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了一个。第二天早上又将剩下的桃子吃掉一半,又多吃了一个。以后每天早上都吃了前一天剩下的一半后又多吃一个。到第10天早上想再吃时,见只剩下一个桃子了。
求第一天共摘了多少个桃子?
(1)编程思路。
设x[n]表示第n天吃桃子前的桃子数,则有x[10]=1。
由于, x[i]=x[i-1]-x[i-1]/2-1,
因此,递推关系式为: x[i-1]=2*(x[i]+1)。倒推求得x[1]就是猴子所摘的桃子数。
(2)源程序。
#include
using namespace std;
int main()
{
int a\[11\],i;a\[10\]=1;for (i=9;i>=1;i--)a\[i\]=2\*(a\[i+1\]+1);cout<<a\[1\]<<endl;return 0;
}
(3)问题扩展。有一猴子第一天摘下若干个桃子,当即吃了一半,还不过瘾,又多吃了m个。第二天早上又将剩下的桃子吃掉一半,又多吃了m个。以后每天早上都吃了前一天剩下的一半后又多吃m个。到第n天早上想再吃时,见只剩下d个桃子了。求第一天共摘了多少个桃子(m,n,d均由键盘输入,且1<=n,m,d<=20)?(4)扩展问题的源程序。
#include
using namespace std;
int main()
{
int i,m,n,d;cin>>n>>m>>d;int \*a;a=new int \[n+1\];a\[n\]=d;for (i=n-1;i>=1;i--)a\[i\]=2\*(a\[i+1\]+m);cout<<a\[1\]<<endl;return 0;
}
【例5】过河卒
如图3,在棋盘的A点有一个过河卒,需要走到目标B点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如图4-4的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如,图4-4中C点上的马可以控制9个点(图中的P1,P2,…,P8 和C)。卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n,m)(n,m为不超过50的整数,并由键盘输入),同样马的位置坐标通过键盘输入,并约定C<>A,同时C<>B。编写程序,计算出卒从A点能够到达B点的路径的条数。例如,输入6 6 3 2,输出为17。
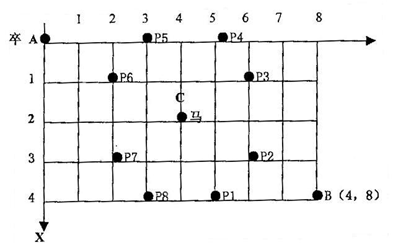
图3 棋盘上的过河卒和对方的控制马
(1)编程思路。
在棋盘的A点(0,0)的过河卒要到达棋盘上的任意一点,只能从左边和上边两个方向过来。因此,要到达某一点的路径数,等于和它相邻的左、上两个点的路径数和:F\[i\]\[j\] = F\[i-1\]\[j\] + F\[i\]\[j-1\]。可以使用逐列(或逐行)递推的方法来求出从起始顶点到终点的路径数目,即使有障碍(将马的控制点称为障碍),这一递推方法也完全适用,只要将到达该点的路径数目设置为0即可,用F\[i\]\[j\]表示到达点(i,j)的路径数目,g\[i\]\[j\]表示点(i,j)有无障碍,递推方程如下:
F[0][0] = 1 初始点直接可达。
F[i][0] = F[i-1][0] (i > 0,g[i][0] =0) // 左边界
F[0][j] = F[0][j-1] (j > 0,g[0][j] = 0) // 上边界
F[i][j] = F[i-1][j] + F[i][j-1] (i > 0,j > 0,g[x, y] = 0) // 递推式
(2)源程序。
#include
using namespace std;
int main()
{
int i,j,x,y,n,m,forbidden\[51\]\[51\];int ans\[51\]\[51\];int dx\[8\]=\{-2,-1,1,2,2,1,-1,-2\};int dy\[8\]=\{1,2,2,1,-1,-2,-2,-1\};cin>>n>>m>>x>>y;for (i=0;i<=n;i++)for (j=0;j<=m;j++)\{forbidden\[i\]\[j\]=0;ans\[i\]\[j\]=0;\}ans\[0\]\[0\]=1;forbidden\[x\]\[y\]=1;for (i=0;i<8; i++)if (x+dx\[i\]>=0 && x+dx\[i\]<=n && y+dy\[i\]>=0 && y+dy\[i\]<=m)forbidden\[x+dx\[i\]\]\[y+dy\[i\]\]=1;for (i=1; i<=n; i++)if (forbidden\[i\]\[0\]==0)ans\[i\]\[0\]=1;else break;for (i=1; i<=m; i++)if (forbidden\[0\]\[i\]==0)ans\[0\]\[i\]=1;else break;for (i=1; i<=n; i++)for (j=1; j<=m; j++)if (forbidden\[i\]\[j\]==0)ans\[i\]\[j\]=ans\[i-1\]\[j\]+ans\[i\]\[j-1\];cout<<ans\[n\]\[m\]<<endl;return 0;
}
【例6】学生队列。
There are many students in PHT School. One day, the headmaster whose name is PigHeader wanted all students stand in a line. He prescribed that girl can not be in single. In other words, either no girl in the queue or more than one girl stands side by side.
The case n=4 (n is the number of children) is like FFFF, FFFM, MFFF, FFMM, MFFM, MMFF, MMMM Here F stands for a girl and M stands for a boy. The total number of queue satisfied the headmaster’s needs is 7.
Can you make a program to find the total number of queue with n children?
(1)编程思路。设满足要求的n个学生的队列数为F(n)表示。简单枚举n较小的情况为:F(0)=1 (没有人也是合法的,这个可以特殊处理,就像0的阶乘定义为1一样);F(1)=1(一个男生M);F(2)=2;(两个男生MM或两个女生FF);F(3)=4(MMM、MFF、FFM或FFF)。当人数n大于3时,n个学生排队可以看成是由n-1个学生排好队后再加一个学生。按最后加的学生的性别分两种情况:1)当加的最后一个学生是男孩M时候,前面n-1个随便排出来,只要符合要求就可以,即方案数为F(n-1)。2)当加的最后一个学生是女孩F时候,第n-1个学生肯定是女孩F,这时候又有两种情况:① 前面n-2个学生按满足要求的方法排好队,后面加两个女生一定也满足要求,此时方案数为F(n-2)。② 前面n-2个人不是满足要求的队列,加上两个女生也有可能是合法的。当第n-2个学生是女孩而第n-3个学生是男孩时,后面加上两个女孩可能合法。此时前n-4个学生的队列必须满足要求,即方案数为F(n-4)。综上所述:总数F(n)= F(n-1)+ F(n-2)+ F(n-4)。(2)源程序。
#include
using namespace std;
int main()
{
int i,n,f\[31\];f\[0\]=1; f\[1\]=1; f\[2\]=2; f\[3\]=4;for(i=4;i<=30;i++)f\[i\]=f\[i-1\]+f\[i-2\]+f\[i-4\]; // 按递推关系实施递推while (cin>>n && n!=-1)\{cout<<f\[n\]<<endl;\}return 0;
}
【例7】栈
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。栈有两种最重要的操作,即pop(从栈顶弹出一个元素)和push(将一个元素进栈)。栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。晶晶宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而她自己无法给出答案,所以需要你的帮忙。晶晶考虑的是这样一个问题:一个操作数序列,从1,2,一直到n(图4-5所示为1到3的情况),栈A的深度大于n。
现在可以进行两种操作,
1)将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的push操作)。
2)将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的pop操作)。
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列。设栈的原始状态如图4所示,由123生成序列231的过程如图5所示。
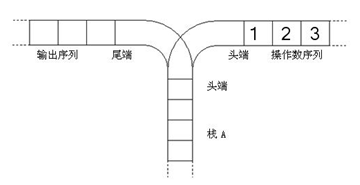
图4 栈的原始状态
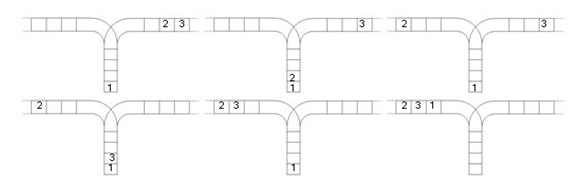
图5 采用栈生成序列231的过程
请编写程序,对输入的n,计算并输出由操作数序列1,2,…,n经过栈操作可能得到的输出序列的总数。(1)编程思路。先模拟入栈、出栈操作,看看能否找出规律,设f(n)表示n个数通过栈操作后的排列总数,当n很小时,很容易模拟出f(1)=1,f(2)=2,f(3)=5。通过观察,看不出它们之间的递推关系,再分析n=4的情况,假设入栈前的排列为“4123”,按第一个数“4”在出栈后的位置进行分情况讨论:1)若“4”最先输出,刚好与n=3相同,总数为f(3)。2)若“4”第二个输出,则在“4”的前只能是“1”,“23”在“4”的后面,这时可以分别看作是n=1和n=2时的两种情况,排列数分别为f(1)和f(2),所以此时的总数为f(1)\*f(2)。3)若“4”第三个输出,则“4”的前面二个数为“12”,后面一个数为“3”,组成的排列总数为f(2)\*f(1)。4)若“4”第四个输出,与情况(1)相同,总数为f(3)。所以有:f(4)=f(3)+f(1)\*f(2)+f(2)\*f(1)+f(3)。若设0个数通过栈后的排列总数为:f(0)=1;上式可变为:f(4)=f(0)\*f(3)+f(1)\*f(2)+f(2)\*f(1)+f(3)\*f(0)。
再进一步推导,不难推出递推式:
f(n)=f(0)*f(n-1)+f(1)*f(n-2)+…+f(n-1)*f(0);
即f(n)= (n>=1)
初始值:f(0)=1;
有了以上递推式,就很容易用递推法写出程序。
(2)源程序。
#include
using namespace std;
int main()
{
int a\[19\]=\{0\},n,i,j;cin>>n;a\[0\]=1;for (i=1;i<=n;i++)for (j=0;j<=i-1;j++)a\[i\]=a\[i\]+a\[j\]\*a\[i-j-1\];cout<<a\[n\]<<endl;return 0;
}
(3)用公式直接求解。实际上,一个栈的入栈序列为1,2,3,…,n,其不同的出栈序列的种数是一个卡特兰数。卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。该数列如下:
C0=1,C1=1,C2=2,C3=5,C4=14,C5=42,C6=132,C7=429,C8=1430,
C9=4862,C10=16796,C11=58786,C12=208012,……。
卡塔兰数的一般项公式为:
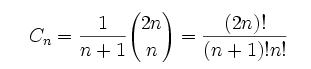
Cn的另一个表达形式为:
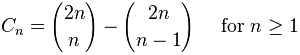
下面简要描述一下这个公式的推导情况。
对于1~n中的每一个数来说,必须入栈一次、出栈一次。设入栈为状态“1”,出栈为状态“0”。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1~n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目等于由左至右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左至右扫描,0的累计数大于1的累计数)的方案数即为所求。不符合要求的数的特征是由左至右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如果把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。 即不符合要求的方案数为c(2n,n+1)。由此得出,输出序列的总数目= c(2n,n)-c(2n,n+1)=c(2n,n)/(n+1)。(4)采用公式直接求解的源程序。
#include
using namespace std;
int combin(int n,int m) // 求组合数C(n,m)
{
int p=1,i,t;t=n;for (i=1;i<=m;i++)\{p=p\*t/i;t--;\}return p;
}
int main()
{
int n;cin>>n;cout<<combin(2\*n,n)/(n+1)<<endl;return 0;
}
【例8】整数划分问题
正整数s(简称为和数)的划分(又称拆分)是把s分成为若干个正整数(简称为零数或部分)之和,划分式中允许零数重复,且不记零数的次序。试求s=12共有多少个不同的划分式?展示出所有这些划分式。
(1)编程思路。
整数划分问题可采用多种方法解决,下面我们采用递推的法来完成。
为了建立递推关系,先对和数k较小时的划分式作观察归纳:
k=2:1+1;2 2种划分式
k=3:1+1+1;1+2;3 3种划分式
k=4:1+1+1+1;1+1+2;1+3;2+2;4 5种划分式
k=5:1+1+1+1+1;1+1+1+2;1+1+3;1+2+2;1+4;2+3;5 7种划分式
由以上各划分看到,除和数本身k=k这一特殊划分式外,其它每一个划分式至少为两项之和。约定在所有划分式中零数作非降序排列,探索和数k的划分式与和数k−1的划分式存在以下递推关系:1)在所有和数k−1的划分式前加零数1都是和数k的划分式。2)和数k−1的划分式的前两个零数作比较,如果第1个零数x1小于第2个零数x2,则把第1个零数加1后成为和数k的划分式。
定义一个三维数组a,a[k][j][i]表示为和数k的第j个划分式的第i个数。
递推的初始条件为:a[2][1][1]=1; a[2][1][2]=1; a[2][2][1]=2。
根据递推关系,实施递推:
1)实施在k−1所有划分式前加1操作。
a[k][j][1]=1;
for (t=2;t<=k;t++)
a\[k\]\[j\]\[t\]=a\[k−1\]\[j\]\[t−1\]; // k−1的第t−1项变为k的第t项
2)若k−1划分式第1项小于第2项,第1项加1,变为k的第i个划分式
if(a\[k-1\]\[j\]\[1\]<a\[k-1\]\[j\]\[2\]) // 若k-1划分式第1项小于第2项\{ i++; // 第1项加1为k的第i个划分式的第1项a\[k\]\[i\]\[1\]=a\[k-1\]\[j\]\[1\]+1;for(t=2;t<=k-1;t++)a\[k\]\[i\]\[t\]=a\[k-1\]\[j\]\[t\];\}
(2)源程序及运行结果。
#include
#include
using namespace std;
int main()
{
int s,i,j,k,t,cnt;static int a\[21\]\[800\]\[21\]=\{0\};cout<<"input s(s<=20):";cin>>s;a\[2\]\[1\]\[1\]=1; a\[2\]\[1\]\[2\]=1; a\[2\]\[2\]\[1\]=2;cnt=2;for(k=3;k<=s;k++)\{for(j=1;j<=cnt;j++)\{a\[k\]\[j\]\[1\]=1;for(t=2;t<=k;t++) // 实施在k-1所有划分式前加1操作a\[k\]\[j\]\[t\]=a\[k-1\]\[j\]\[t-1\];\}for(i=cnt,j=1;j<=cnt;j++)if(a\[k-1\]\[j\]\[1\]<a\[k-1\]\[j\]\[2\]) // 若k-1划分式第1项小于第2项\{i++; // 第1项加1为k的第i个划分式的第1项a\[k\]\[i\]\[1\]=a\[k-1\]\[j\]\[1\]+1;for(t=2;t<=k-1;t++)a\[k\]\[i\]\[t\]=a\[k-1\]\[j\]\[t\];\}i++; a\[k\]\[i\]\[1\]=k; // k的最后一个划分式为:k=kcnt=i;\}for(j=1;j<=cnt;j++) // 输出s的所有划分式\{cout<<setw(4)<<j<<": "<<s<<"="<<a\[s\]\[j\]\[1\];i=2;while (a\[s\]\[j\]\[i\]>0)\{cout<<"+"<<a\[s\]\[j\]\[i\];i++;\}cout<<endl;\}return 0;
}
(3)整数划分的优化。上面递推算法的时间复杂度与空间复杂度为O(n2u),其中u为n划分式的个数。由于u随n增加非常快,难以估算其数量级,因此算法的时间复杂度与空间复杂度是很高的。下面我们对整数划分进行集智。分析上面使用三维数组a\[k\]\[j\]\[i\]完成的递推过程。当由k−1的划分式推出k的划分式时,k−1以前的数组单元已完全闲置。因此,可以考虑把三维数组a\[k\]\[j\]\[i\]改进为二维数组a\[j\]\[i\]。进行和数为k的递推前,数组元素a\[j\]\[i\]表示和数是k−1的已有划分式。根据递推关系推出和数为k的划分式:1)把a\[j\]\[i\]依次存储到a\[j\]\[i+1\],加上第一项a\[j\]\[1\]=1;这样完成在k−1的所有划分式前加1的操作,转化为k的划分式。
for(t=i;t>=1;t−−)
a\[j\]\[t+1\]=a\[j\]\[t\];
a[j][1]=1;
2)对已转化的cnt个划分式逐个检验,若其第2个数小于第3个数(相当于k−1时的第1个数小于第2个数),则把第2个数加1,去除第一个数后,作为k时增加的一个划分式,为第t个(t从cnt开始,每增加一个划分式,t增1)划分式。
for(t=u,j=1;j<=u;j++)
if(a(j,2)<a(j,3)) // 若k−1划分式第1项小于第2项
\{t++;a(t,1)=a(j,2)+1; // 第1项加1 作为k的第t个划分式的第1项i=3;while(a(j,i)>0)\{a(t,i−1)=a(j,i);i++;\}\}(4)优化后的源程序。
#include
#include
using namespace std;
int main()
{
int s,i,j,k,t,cnt;static int a\[1600\]\[25\]=\{0\};cout<<"input s(s<=24):";cin>>s;a\[1\]\[1\]=1;a\[1\]\[2\]=1;a\[2\]\[1\]=2;cnt=2;for(k=3;k<=s;k++)\{for(j=1;j<=cnt;j++)\{i=k-1;for(t=i;t>=1;t--) // 实施在k-1所有划分式前加1操作a\[j\]\[t+1\]=a\[j\]\[t\];a\[j\]\[1\]=1;\}for(t=cnt,j=1;j<=cnt;j++)if(a\[j\]\[2\]<a\[j\]\[3\]) // 若k-1划分式第1项小于第2项\{t++;a\[t\]\[1\]=a\[j\]\[2\]+1; // 第1项加1i=3;while(a\[j\]\[i\]>0)\{a\[t\]\[i-1\]=a\[j\]\[i\];i++;\}\}t++; a\[t\]\[1\]=k; // 最后一个划分式为:k=kcnt=t;\}for(j=1;j<=cnt;j++) // 输出s的所有划分式\{cout<<setw(4)<<j<<": "<<s<<"="<<a\[j\]\[1\];i=2;while (a\[j\]\[i\]>0)\{cout<<"+"<<a\[j\]\[i\];i++;\}cout<<endl;\}return 0;
}
改进的递推程序把原有的三维数组优化为二维数组,降低了算法的空间复杂度,拓展了算法的求解范围。但是,由于划分式的数量cnt随和数s增加得相当迅速。例如,和数为24时有1575种划分。因此尽管改进为二维数组,求解的和数s也不可能太大。
转载于 //www.cnblogs.com/cs-whut/p/11022612.html
//www.cnblogs.com/cs-whut/p/11022612.html





























还没有评论,来说两句吧...