最小生成树

Jungle Roads

http://poj.org/problem?id=1251

Description

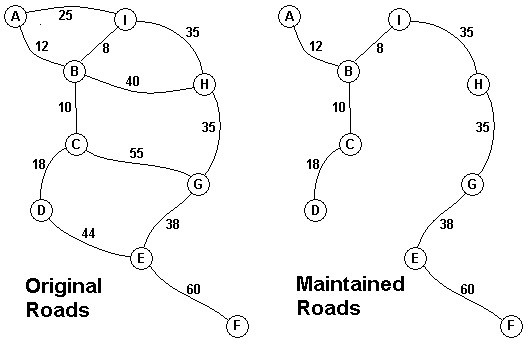
The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems.

Input

The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above.

Output

The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit.

Sample Input

9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0

Sample Output

216
30

标准最小生成树，用了简化版的Prim算法，也可以用Kruskal算法

1 #include <stdio.h>
 2 #include <string.h>
 3 #include <algorithm>
 4 #define maxn 65535
 5 using namespace std;
 6 int MG[1005][1005];
 7 int F[1005];
 8 
 9 int main()
10 {
11     //freopen("sample.txt","r",stdin);
12     int n;
13     while(~scanf("%d",&n)&&n)
14     {
15         int sum=0,i;
16         memset(MG,0,sizeof(MG));
17         for(i=0;i<n-1;i++)
18         {
19             char c;
20             scanf(" %c",&c);
21             int a;
22             scanf("%d",&a);
23             for(int j=0;j<a;j++)
24             {
25                 char k;
26                 int b;
27                 scanf(" %c",&k);
28                 scanf("%d",&b);
29                 MG[c-'A'][k-'A']=b;
30                 MG[k-'A'][c-'A']=b;
31             }
32             F[i]=maxn;
33         }
34         F[i]=maxn;
35         F[0]=0;
36         for(i=1;i<n;i++)
37         {
38             if(MG[0][i])
39             {
40                 F[i]=MG[0][i];
41             }
42         }
43         for(i=1;i<n;i++)
44         {
45             int m=maxn,t;
46             for(int g=0;g<n;g++)
47             {
48                 if(F[g]&&F[g]<m)
49                 {
50                     t=g;
51                     m=F[g];
52                 }
53             }
54             sum+=F[t];
55             F[t]=0;
56             for(int j=1;j<n;j++)
57             {
58                 if(F[j]&&MG[t][j])
59                 {
60                     F[j]=min(MG[t][j],F[j]);
61                 }
62             }
63         }
64         printf("%d\n",sum);
65     }
66     return 0;
67 }