最小生成树-蒲公英云

最小生成树

末蓝、 2022-09-20 15:18 310阅读 0赞

最小生成树定义：

在一给定的无向图 G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即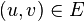 $(u, v)\\in E$ ），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即 $T\\subseteq E$ ）且为无循环图，使得 $w(T) = \\sum\_\{(u,v)\\in T\} w(u,v)$ 的 w(T) 最小，则此 T 为 G 的最小生成树。

最小生成树其实是最小权重生成树的简称。

性质：

最小生成树的边数必然是顶点数减一，|E| = |V| - 1。
最小生成树不可以有循环。
最小生成树不必是唯一的。

算法；

Prim算法与Kruskal算法是寻找最小生成树的经典方法，两者皆为贪心法，通常使用二元堆积，时间复杂度为 $O(E\\lg V)$ 。若使用斐波那契堆，Prim算法可加速至 $O(E + V\\lg V)$ 。
注：以上内容来自维基百科（为2014年6月19日 (星期四) 12:01修订后结果）

接下来，博主采用的是prim算法，用的是邻接矩阵，算法复杂度为o（V^2)（V为点组成的集合），具体的prim算法请点“Prim算法”

后面博主又补充了Kruskal算法，其实还有Borůvka’s algorithm，后续补充吧…..

源代码如下：

以下代码图中的点不得超过104个，单边权值不得超过1000000

#include<stdio.h>
#define N 105
#define INF 1000000
int map[N][N],visit[N],dis[N];
int main()
{
    int n,x,y,value,i,j;
    scanf("%d",&n);//输入的图的点不超过104个 
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        map[i][j]=INF;
        visit[i]=0;
    }
    while(scanf("%d%d%d",&x,&y,&value)==3&&x&&y&&value）//输入图中点的关系 
    {
        map[x][y]=value;
        map[y][x]=value;//输入的图中的点的关系默认为双向的 
    }
    visit[1]=1;//默认从点1开始，把点1移向集合V 
    int m_coor=0,min=INF;
    for(i=2;i<=n;i++)
    {
        dis[i]=map[1][i];
        if(min>dis[i])
        {
            min=dis[i];
            m_coor=i;//找出下一个移向集合V的点的坐标    
        }
    }
    visit[m_coor]=1;//标记该点移到了集合V 
    if(min==INF)
    {    
        printf("No minimum spanning tree!\n");
        return 0;
    }//集合V中的点与集合E中的点不连接，图不是连通的，因此不存在最小生成树 
    int count=n-1;
    while(count-->0)//将右侧集合中的点依次移到左侧集合 
    {
        for(i=2;i<=n;i++)
        if(visit[i]==0)
        {
            if(dis[i]>map[m_coor][i])
            dis[i]=map[m_coor][i];
        }
        min=INF;
        for(i=2;i<=n;i++)
        if(visit[i]==0&&min>dis[i])
        {
            min=dis[i];
            m_coor=i;    
        }
        if(min==INF)
        {    
            printf("No minimum spanning tree!\n");
            return 0;
        }
        visit[m_coor]=1;
    }
    int sum=0;
    for(i=2;i<=n;i++)
    sum+=dis[i];
    printf("%d\n",sum);//输出最小生成树 
    return 0;
}

改进后的prim，更整齐

#include<cstdio>                                                                    
#include<cstring>                                                                   
#include<iostream>                                                                  
#define mini 1000005                                                                
#define N 105                                                                       
using namespace std;                                                                
int dis[N][N],dist[N],sign[N];                                                      
void intial()                                                                       
{                                                                                   
    for(int i=0;i<N;i++)                                                               
    {                                                                                  
        dist[i]=mini;                                                                     
        sign[i]=0;                                                                        
    }                                                                                  
}                                                                                   
int main()                                                                          
{                                                                                   
    int n;                                                                             
//    freopen("in.txt","r",stdin);                                                     
//    freopen("out1.txt","w",stdout);                                                  
    while(scanf("%d",&n)!=EOF)                                                         
    {                                                                                  
        int i,j;                                                                          
        for(i=0;i<n;i++)                                                                  
        for(j=0;j<n;j++)                                                                  
        scanf("%d",&dis[i][j]);                                                           
        intial();                                                                         
        int min,m_coor=0,coor=0,time=n-1,sum=0;sign[0]=1;                                 
        while(time--)        //一定是n-1次循环，不然就会出错                                                             
        {                                                                                 
            min=mini;                                                                        
            for(i=1;i<n;i++)                                                                 
            if(!sign[i])                                                                     
            {                                                                                
                if(dist[i]>dis[m_coor][i])dist[i]=dis[m_coor][i];                               
                if(min>dist[i])                                                                 
                {                                                                               
                    min=dist[i];coor=i;                                                            
                }                                                                               
            }                                                                                
            sign[coor]=1;                                                                    
            m_coor=coor;                                                                     
            sum+=min;                                                                        
        }                                                                                 
        printf("%d\n",sum);                                                               
    }                                                                                  
    return 0;                                                                          
}

kruskal算法求最小生成树

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
using namespace std;
const int maxn=1000000;
int pa[maxn];
struct Eage
{
    int x,y,longth;
    void read()
    {
        scanf("%d%d%d",&x,&y,&longth);
    }
    bool operator < (const Eage &t)const 
    {
        return longth<t.longth;
    }
};
Eage eage[maxn];
void initial(int n)
{
    for(int i=0;i<=n;i++)
    pa[i]=i;
}
int find(int x)
{
    return x==pa[x]? x:(pa[x]=find(pa[x]));
}
bool Merge(int x,int  y)
{
    int px=find(x),py=find(y);
    if(px!=py)
    {
        pa[px]=py;
        return true;
    }
    return false;
}
/*bool cmp(Eage a,Eage b)
{
    return a.longth<b.longth;
}*/
int main()
{
    int n,m;
    while(scanf("%d%d",&n)==2&&n)
    {
        initial(n);
        for(int i=0;i<m;i++)
        eage[i].read();
        //scanf("%d%d%d",&eage[i].x,&eage[i].y,&eage[i].longth);
        int sum=0,count=0;
        sort(eage,eage+m);
        for(int i=0;i<m;i++)
        {
            if(Merge(eage[i].x,eage[i].y))
                {
                    sum+=eage[i].longth;
                    count++;
                }
        }
        if(count!=n-1)printf("No minimum spaning tree!\n");
        else printf("%d\n",sum);    
    }    
    return 0;
}