最小生成树
kruskal算法基本思路:先对边按权重从小到大排序,先选取权重最小的一条边,如果该边的两个节点均为不同的分量,则加入到最小生成树,否则计算下一条边,直到遍历完所有的边。
prim算法基本思路:所有节点分成两个group,一个为已经选取的selected_node(为list类型),一个为candidate_node,首先任取一个节点加入到selected_node,然后遍历头节点在selected_node,尾节点在candidate_node的边,选取符合这个条件的边里面权重最小的边,加入到最小生成树,选出的边的尾节点加入到selected_node,并从candidate_node删除。直到candidate_node中没有备选节点(这个循环条件要求所有节点都有边连接,即边数要大于等于节点数-1,循环开始前要加入这个条件判断,否则可能会有节点一直在candidate中,导致死循环)。
class Graph(object):def __init__(self, maps):self.maps = mapsself.nodenum = self.get_nodenum()self.edgenum = self.get_edgenum()def get_nodenum(self):return len(self.maps)def get_edgenum(self):count = 0for i in range(self.nodenum):for j in range(i):if self.maps[i][j] > 0 and self.maps[i][j] < 9999:count += 1return countdef kruskal(self):res = []if self.nodenum <= 0 or self.edgenum < self.nodenum-1:return resedge_list = []# 先对于所有的边按照权重大小进行排序for i in range(self.nodenum):for j in range(i+1,self.nodenum):if self.maps[i][j] < 9999:edge_list.append([i, j, self.maps[i][j]])#按[begin, end, weight]形式加入edge_list.sort(key=lambda a:a[2])#已经排好序的边集合# 对排序好的数组从小到大进行排序,如果没有存在,那么添加到最后的列表中# 如果已经连通了,那么不执行操作group = [[i] for i in range(self.nodenum)]for edge in edge_list:for i in range(len(group)):if edge[0] in group[i]:m = iif edge[1] in group[i]:n = iif m != n:res.append(edge)group[m] = group[m] + group[n]group[n] = []print(group)return resdef prim(self):res = []if self.nodenum <= 0 or self.edgenum < self.nodenum-1:return resres = []# 设置已经存在的结点集合和待用的结点集合# 找到已经存在的结点到待用结点集合中的所有结点的权重的最小值# 执行相应的删除和添加操作seleted_node = [0]candidate_node = [i for i in range(1, self.nodenum)]while len(candidate_node) > 0:begin, end, minweight = 0, 0, 9999for i in seleted_node:for j in candidate_node:if self.maps[i][j] < minweight:minweight = self.maps[i][j]begin = iend = jres.append([begin, end, minweight])seleted_node.append(end)candidate_node.remove(end)return resmax_value = 9999row0 = [0,7,max_value,max_value,max_value,5]row1 = [7,0,9,max_value,3,max_value]row2 = [max_value,9,0,6,max_value,max_value]row3 = [max_value,max_value,6,0,8,10]row4 = [max_value,3,max_value,8,0,4]row5 = [5,max_value,max_value,10,4,0]maps = [row0, row1, row2,row3, row4, row5]graph = Graph(maps)print('邻接矩阵为\n%s'%graph.maps)print('节点数据为%d,边数为%d\n'%(graph.nodenum, graph.edgenum))print('------最小生成树kruskal算法------')print(graph.kruskal())print('------最小生成树prim算法')print(graph.prim())
初始图片:
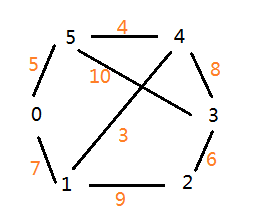
文章转载,原博客地址:https://blog.csdn.net/mashijia986/article/details/79100925
































还没有评论,来说两句吧...