树状数组板子-蒲公英云

树状数组板子

r囧r小猫 2022-03-15 15:22 387阅读 0赞

树状数组重点是在树状的数组

大家都知道二叉树吧

叶子结点代表A数组A[1]~A[8]

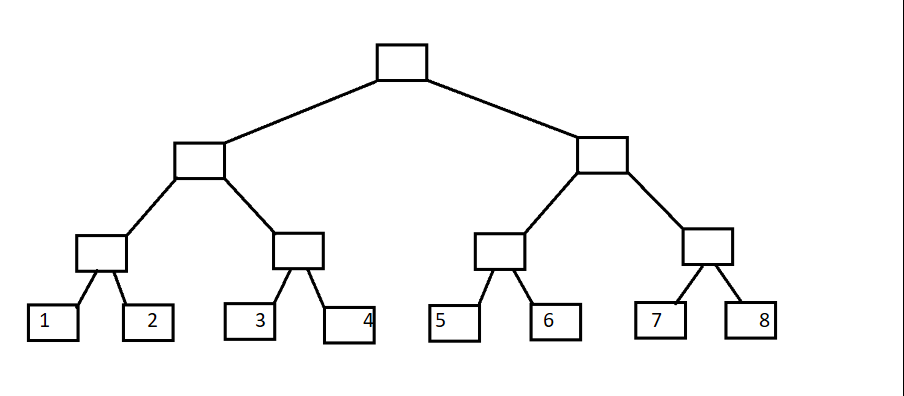
现在变形一下

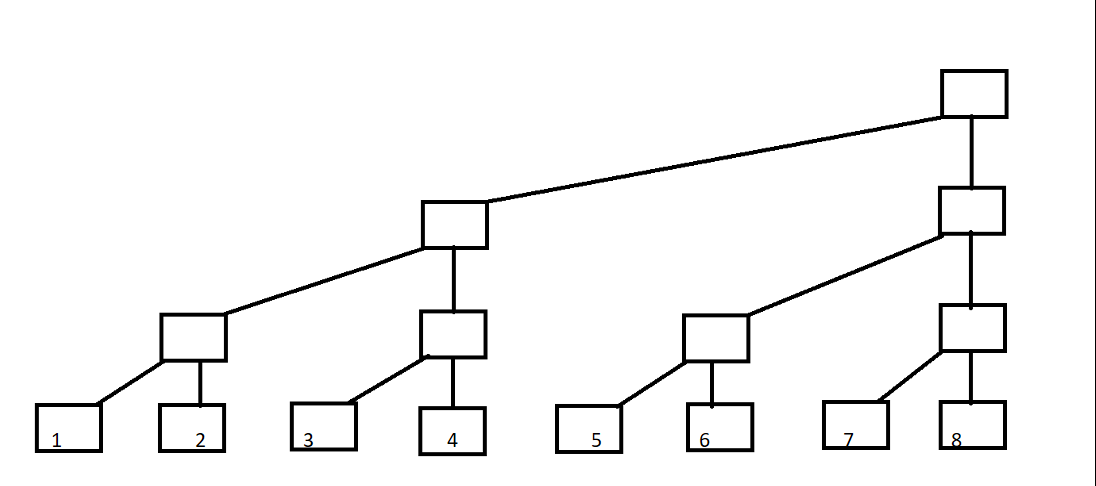
现在定义每一列的顶端结点C[]数组

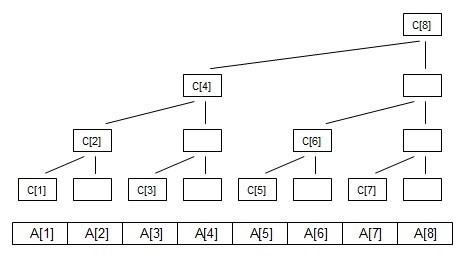
如下图

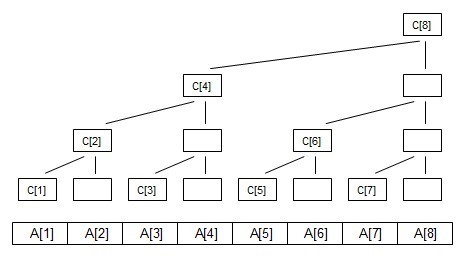
C[i]代表子树的叶子结点的权值之和// 这里以求和举例

如图可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

下面观察如下图

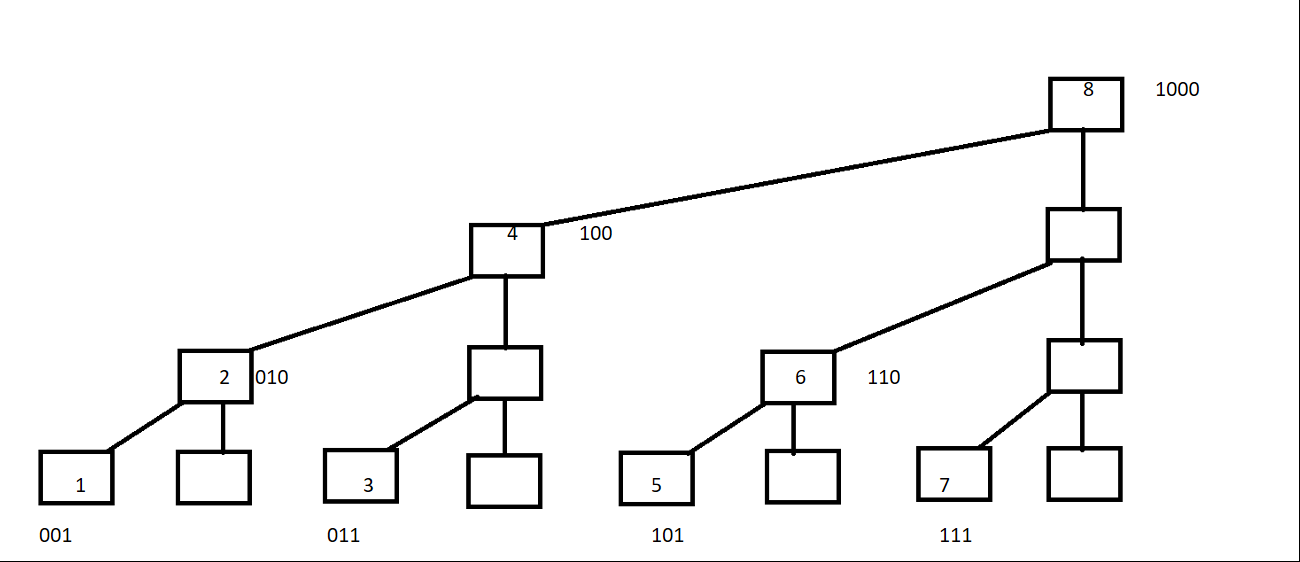
将C[]数组的结点序号转化为二进制

1=(001) C[1]=A[1];

2=(010) C[2]=A[1]+A[2];

3=(011) C[3]=A[3];

4=(100) C[4]=A[1]+A[2]+A[3]+A[4];

5=(101) C[5]=A[5];

6=(110) C[6]=A[5]+A[6];

7=(111) C[7]=A[7];

8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

对照式子可以发现 C[i]=A[i-2^k+1]+A[i-2^k+2]+……A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8时，k=3;

可以自行带入验证;

现在引入lowbit(x)

lowbit(x) 其实就是取出x的最低位1 换言之 lowbit(x)=2^k k的含义与上面相同理解一下

下面说代码

int lowbit(int t)
{
return t&(-t);
}
//-t 代表t的负数计算机中负数使用对应的正数的补码来表示
//例如 :
// t=6（0110）此时 k=1
//-t=-6=(1001+1)=(1010)
// t&(-t)=(0010)=2=2^1

C[i]=A[i-2^k+1]+A[i-2^k+2]+……A[i];

C[i]=**A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+……A[i];**

*************************************************分割线

区间查询

ok 下面利用C[i]数组，求A数组中前i项的和

举个例子 i=7;

sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ; 前i项和

C[4]=A[1]+A[2]+A[3]+A[4]; C[6]=A[5]+A[6]; C[7]=A[7];

可以推出: sum[7]=C[4]+C[6]+C[7];

序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];

再举个例子 i=5

sum[5]=A[1]+A[2]+A[3]+A[4]+A[5] ; 前i项和

C[4]=A[1]+A[2]+A[3]+A[4]; C[5]=A[5];

可以推出: sum[5]=C[4]+C[5];

序号写为二进制: sum[(101)]=C[(100)]+C[(101)];

细细观察二进制树状数组追其根本就是二进制的应用

结合代码

int getsum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=C[i];
return ans；
}

对于i=7 进行演示

                              7(111)     **     ans+=C\[7\]**

lowbit(7)=001 7-lowbit(7)=6(110) ans+=C[6]

lowbit(6)=010 6-lowbit(6)=4(100) ans+=C[4]

lowbit(4)=100 4-lowbit(4)=0(000)

对于i=5 进行演示

                              5(101)     **      ans+=C\[5\]**

lowbit(5)=001 5-lowbit(5)=4(100) ans+=C[4]

lowbit(4)=100 4-lowbit(4)=0(000)

*************************************************分割线

单点更新

当我们修改A[]数组中的某一个值时应当如何更新C[]数组呢？

回想一下区间查询的过程，再看一下上文中列出的图

结合代码分析

void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
tree[i]+=y;
}
//可以发现更新过程是查询过程的逆过程
//由叶子结点向上更新C[]数组

如图：

当更新A[1]时需要向上更新C[1] ,C[2],C[4],C[8]

                 C\[1\],   C\[2\],    C\[4\],     C\[8\]

写为二进制 C[(001)],C[(010)],C[(100)],C[(1000)]

                                  1(001)        **C\[1\]+=A\[1\]**

lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]

lowbit(2)=010 2+lowbit(2)=4(100) C[4]**+=A[1]**

lowbit(4)=100 4+lowbit(4)=8(1000) C[8]**+=A[1]**

洛谷3374模板

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3个整数，表示一个操作，具体如下：

操作1：格式：1 x k 含义：将第x个数加上k

操作2：格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1： 复制

输出样例#1： 复制

14
16
#include<bits/stdc++.h>
using namespace std;
int d[500005],tree[2000005],n,m;
int lowbit(int i){
    return i&-i;
}
void add(int x,int v){
    while(x<=n){
        tree[x]+=v;
        x+=lowbit(x);
    }
}
int sum(int x){
    int ans=0;
    while(x!=0){
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d",&d[i]); 
        add(i,d[i]);
    }
    int a,b,c;
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&a,&b,&c);
        if(a==1)add(b,c);
        else printf("%d\n",sum(c)-sum(b-1));
    }
    return 0;
}