树状数组
目录:
- 概念
- 应用
- 充分性
- 建立树状数组
- 典题分析
一.概念
数组来模拟树形结构。那么、为什么不直接建树?没必要,因为树状数组能处理的问题就没必要建树。和Trie树的构造方式有类似之处。
树状数组介绍
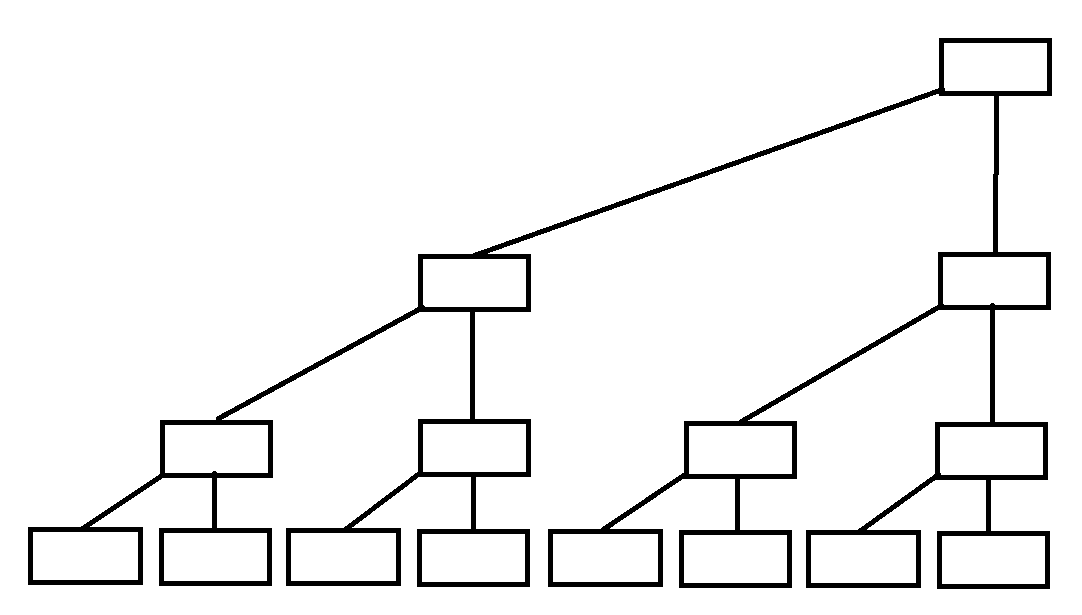
如果每个父亲都存的是两个儿子的值,是不是就可以解决这类区间问题了呢。是的没错,但是这样的树形结构,叫做线段树。
那真的的树形结构是怎样的,和上图类似,但省去了一些节点,以达到用数组建树。
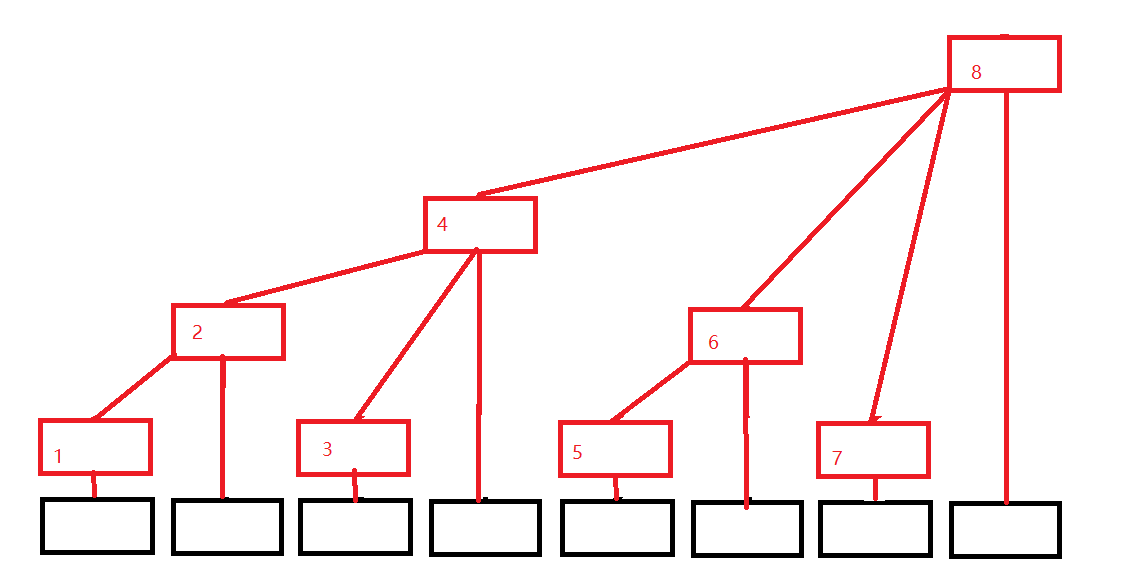
黑色数组代表原来的数组(下面用A[i]代替),红色结构代表我们的树状数组(下面用C[i]代替),发现没有,每个位置只有一个方框,令每个位置存的就是子节点的值的和,则有
- C[1] = A[1];
- C[2] = A[1] + A[2];
- C[3] = A[3];
- C[4] = A[1] + A[2] + A[3] + A[4];
- C[5] = A[5];
- C[6] = A[5] + A[6];
- C[7] = A[7];
- C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
这里有一个有趣的性质:
设节点编号为x,那么这个节点管辖的区间为2^k个元素(其中k为x二进制末尾0的个数)。因为这个区间最后一个元素必然为Ax,所以很明显:Cn = A(n – 2^k + 1) + … + An
例如i = 8(1000)时候,k = 3,可自行验证。C[8]=C[7] + C[6] + C[4];
这个怎么实现求和呢,比如我们要找前7项和,那么应该是SUM = C[7] + C[6] + C[4];
而根据上面的式子,容易的出SUMi = C[i] + C[i-2k1] + C[(i - 2k1) - 2k2] + …..;
其实树状数组就是一个二进制上面的应用。
现在新的问题来了2^k该怎么求呢,不难得出2^k = i&(i^(i-1));但这个还是不好求出呀,前辈的智慧就出来了,2^k = i&(-i);
为什么呢?
这里利用的负数的存储特性,负数是以补码存储的,对于整数运算 x&(-x)有
● 当x为0时,即 0 & 0,结果为0;
●当x为奇数时,最后一个比特位为1,取反加1没有进位,故x和-x除最后一位外前面的位正好相反,按位与结果为0。结果为1。
●当x为偶数,且为2的m次方时,x的二进制表示中只有一位是1(从右往左的第m+1位),其右边有m位0,故x取反加1后,从右到左第有m个0,第m+1位及其左边全是1。这样,x& (-x) 得到的就是x。
●当x为偶数,却不为2的m次方的形式时,可以写作x= y * (2^k)。其中,y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时,x的二进制表示最右边有k个0,从右往左第k+1位为1。当对x取反时,最右边的k位0变成1,第k+1位变为0;再加1,最右边的k位就又变成了0,第k+1位因为进位的关系变成了1。左边的位因为没有进位,正好和x原来对应的位上的值相反。二者按位与,得到:第k+1位上为1,左边右边都为0。结果为2^k。
总结一下:x&(-x),当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。而且这个有一个专门的称呼,叫做lowbit,即取2^k。
#
二.应用
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
这种数据结构(算法)并没有C++和Java的库支持,需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组和线段树很像,但能用树状数组解决的问题,基本上都能用线段树解决,而线段树能解决的树状数组不一定能解决。相比较而言,树状数组效率要高很多。
三.充分性
很容易知道C8表示A1~A8的和,但是C6却是表示A5~A6的和,为什么会产生这样的区别的呢?或者说发明她的人为什么这样区别对待呢?
答案是,这样会使操作更简单!看到这相信有些人就有些感觉了,为什么复杂度被log了呢?可以看到,C8可以看作A1~A8的左半边和+右半边和,而其中左半边和是确定的C4,右半边其实也是同样的规则把A5~A8一分为二……继续下去都是一分为二直到不能分树状数组巧妙地利用了二分,树状数组并不神秘,关键是巧妙!
四.建立树状数组
import java.util.Arrays;public class BinaryIndexTree {static int[] c;int n;public BinaryIndexTree(int n) {this.n = n;c = new int[n+1];}int lowbit(int x) {return x & (x ^ (x-1));}/*** 更新一个元素,初始数组c都是0,所以可以用这个方法初始化c,这时候增加与更新是等价的* @param p 更新第p个元素,索引从1开始* @param d 增加的值,不是更新后的值*/void update(int p, int d) {while (p <= n) {c[p] += d;p += lowbit(p);}}/*** 计算从第一个元素到第p个元素的和* @param p* @return*/int sum(int p) {int ret = 0;while (p > 0) {ret += c[p];p -= lowbit(p);}return ret;}/*** 计算从第s个元素到第e个元素的和* @param s* @param e* @return*/int sum(int s, int e){if(s > n || e < 1 || s > e || s < 1 || e > n){System.out.println("input error!");return -1;}return sum(e) - sum(s - 1);}public static void main(String[] args) {int[] numbers = {1,2,3,4,5,6,7,8,9};BinaryIndexTree bit = new BinaryIndexTree(numbers.length);for (int i=0; i<numbers.length; i++) {bit.update(i+1, numbers[i]);}System.out.println( Arrays.toString(c));System.out.println("1-6的和为:"+bit.sum(6));//第三个元素 +4后bit.update(3, 4);System.out.println( "第三个元素 +4后:"+Arrays.toString(c));System.out.println("第三个元素 +4后.2-6的和为:"+bit.sum(2,6));}}
测试结果如下:
[0, 1, 3, 3, 10, 5, 11, 7, 36, 9]1-6的和为:21第三个元素 +4后:[0, 1, 3, 7, 14, 5, 11, 7, 40, 9]第三个元素 +4后.2-6的和为:24
五.典题分析
- 给定一个初始值都为0的序列,动态地修改一些位置上的数字,加上一个数,减去一个数,或者乘上一个数,然后动态地提出问题,问题的形式是求出一段数字的和.
- 求n个数中 k组提问 从t到t1个数字之和
































还没有评论,来说两句吧...