图像的矩

r囧r小猫 2022-03-21 02:11 250阅读 0赞

## 原理 ##

*  图像的矩是对图像特征描述的一个量，大小为  M × N M \\times N M×N 图像可以看成二维的随机变量 ( x , y ) (x,y) (x,y)

从而定义二维的 ( p + q ) (p+q) (p\+q)的空间矩为： m p q = ∑ 0 M − 1 ∑ 0 N − 1 x p y q f ( x , y )            其 中 p ， q 是 0 , 1 , 2... 整 数 m\_\{pq\}=\\sum\_\{0\}^\{M-1\} \\sum\_\{0\}^\{N-1\} \{x^py^qf(x,y)\} \\space \\space \\space \\space \\space \\space \\space \\space \\space \\space 其中p，q是0,1,2...整数 mpq=0∑M−10∑N−1xpyqf(x,y)          其中p，q是0,1,2...整数

m 00 = ∑ 0 M − 1 ∑ 0 N − 1 f ( x , y )    相 当 于 总 质 量 m\_\{00\}=\\sum\_\{0\}^\{M-1\} \\sum\_\{0\}^\{N-1\} \{f(x,y)\}\\space\\space 相当于总质量 m00=0∑M−10∑N−1f(x,y)  相当于总质量  
 m 01 = ∑ 0 M − 1 ∑ 0 N − 1 y f ( x , y ) ，    m 10 = ∑ 0 M − 1 ∑ 0 N − 1 x f ( x , y ) ， x ˉ = m 10 m 00      y ˉ = m 01 m 00      ( x ˉ , y ˉ ) 相 当 于 质 心 m\_\{01\}=\\sum\_\{0\}^\{M-1\} \\sum\_\{0\}^\{N-1\} y\{f(x,y)\}，\\space \\space m\_\{10\}=\\sum\_\{0\}^\{M-1\} \\sum\_\{0\}^\{N-1\} x\{f(x,y)\}，\\bar\{x\}=\\frac\{m\_\{10\}\}\{m\{\_\{00\}\}\}\\space \\space \\space \\space \\bar\{y\}=\\frac\{m\_\{01\}\}\{m\{\_\{00\}\}\} \\space \\space \\space \\space(\\bar\{x\},\\bar\{y\})相当于质心 m01=0∑M−10∑N−1yf(x,y)，  m10=0∑M−10∑N−1xf(x,y)，xˉ=m00m10    yˉ=m00m01    (xˉ,yˉ)相当于质心

相应的 ( p + q ) (p+q) (p\+q)阶中心矩： μ p q = ∑ 0 M − 1 ∑ 0 N − 1 ( x − x ˉ ) p ( y − y ˉ ) q f ( x , y )            其 中 p ， q 是 0 , 1 , 2... 整 数 \\mu\_\{pq\}=\\sum\_\{0\}^\{M-1\} \\sum\_\{0\}^\{N-1\}\{(x-\\bar\{x\})^p(y-\\bar\{y\})^q\}f(x,y) \\space \\space \\space \\space \\space \\space \\space \\space \\space \\space 其中p，q是0,1,2...整数 μpq=0∑M−10∑N−1(x−xˉ)p(y−yˉ)qf(x,y)          其中p，q是0,1,2...整数  x ˉ = m 10 m 00      y ˉ = m 01 m 00        ( x ˉ , y ˉ ) 相 当 于 质 心 \\bar\{x\}=\\frac\{m\_\{10\}\}\{m\{\_\{00\}\}\}\\space \\space \\space \\space \\bar\{y\}=\\frac\{m\_\{01\}\}\{m\{\_\{00\}\}\} \\space \\space \\space \\space \\space \\space(\\bar\{x\},\\bar\{y\})相当于质心 xˉ=m00m10    yˉ=m00m01      (xˉ,yˉ)相当于质心

归一化的中心矩  η p q \\eta\_\{pq\} ηpq ： η p q = μ p q μ 00 γ         其 中   γ = p + q 2 + 1 ，      p + q = 2 , 3... \\eta\_\{pq\}=\\frac\{\\mu\_\{pq\}\}\{\\mu\_\{00\}^\{\\gamma\}\} \\space \\space \\space \\space \\space \\space \\space 其中 \\space \\gamma=\\frac\{p+q\}\{2\}+1，\\space \\space\\space \\space p+q=2,3... ηpq=μ00γμpq       其中 γ=2p\+q\+1，    p\+q=2,3...

由二阶矩和三阶矩推出以下7个不变矩组（Hu不变矩）：

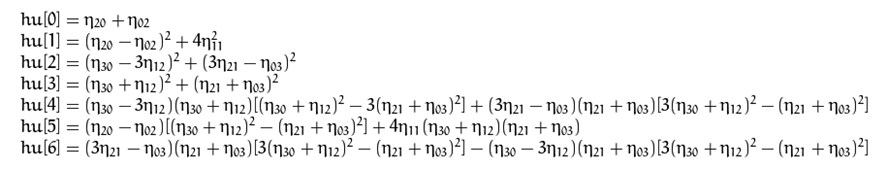
![在这里插入图片描述][20190130100028248.png]  
Hu不变矩对平移、尺度变化、镜像（ h u \[ 6 \] hu\[6\] hu\[6\]符号改变）、和旋转是不变的，可以作为很好的图像的特征。

--------------------

## 代码 ##

#include <opencv2/opencv.hpp>
    #include <iostream>
    
    using namespace cv;
    using namespace std;
    
    Mat src_gray;
    int thresh = 100;
    RNG rng(12345);
    
    void thresh_callback(int, void*);
    
    int main(void)
    { 
    	
        Mat src = imread("../res/test.png");
        if(src.empty())
        { 
    	cout << "can't load the image" << endl;
    	return -1;
        }
    
    
        cv::cvtColor(src, src_gray, cv::COLOR_RGB2GRAY);
        blur(src_gray, src_gray, Size(3,3));
    
        const char* sourec_window = "Source";
        namedWindow(sourec_window);
        imshow(sourec_window, src);
    
        const int MAX_THRESH = 255;
        createTrackbar("Canny thresh:", sourec_window, &thresh, MAX_THRESH, thresh_callback);
        thresh_callback(0,0);
    
    
        waitKey();
    	
    
    	return 0;
    };
    
    
    void thresh_callback(int, void*)
    { 
        Mat canny_output;
        Canny(src_gray, canny_output, thresh, thresh*2, 3);
        vector<vector<Point>> contours;
        cv::findContours(canny_output, contours, cv::RETR_TREE, cv::CHAIN_APPROX_SIMPLE);
    
        vector<Moments> mu(contours.size());
        for(size_t i=0; i<contours.size(); i++)
        { 
    	mu[i] = cv::moments(contours[i]);  //得到每个轮廓的moments ，记录在mu中
        }
    
        vector<Point2f> mc(contours.size());  //每个轮廓的质心
        for(size_t i=0; i<contours.size(); i++)
        { 
    	mc[i] = Point2f(
    		        static_cast<float>(mu[i].m10 / (mu[i].m00 + 1e-5)),
    	        	static_cast<float>(mu[i].m01 / (mu[i].m00 + 1e-5))
    		       ); //利用空间矩来计算质心
    	cout << "mc[" << i << "]=" << mc[i] << endl;
        }
    
        Mat drawing = Mat::zeros(canny_output.size(), CV_8UC3);
        for(size_t i=0; i<contours.size(); i++)
        { 
    	Scalar color = Scalar(rng.uniform(0,256), rng.uniform(0,256), rng.uniform(0,256));
    	cv::drawContours(drawing, contours, (int)i, color, 2); //画出轮廓
    	cv::circle(drawing, mc[i], 4,color,-1);//画出质心
        }
    
        imshow("contours", drawing);
    
    
        for(size_t i=0; i<contours.size(); i++) //打印出由cv::contourArea 和cv::arcLength 计算出来的轮廓面积和周长
        { 
    	cout << "contours[" << i << "]" << "Area(M_00): " << std::fixed << std::setprecision(2) << mu[i].m00 << " " 
    	     << "Area OpenCV API: " << cv::contourArea(contours[i]) << " "<< "length: " << arcLength(contours[i],true)
    	     << endl; 
        }
    
    
    
    }

结果：在中间的部分，质心基本正确，靠近边界的轮廓，质心明显往反向移，这是因为canny处理之后的图，靠近边界的只剩下一弧线，检测轮廓的时候findContours出错，将紧贴弧的**周围一个像素组成的圈**当成轮廓(类似于下图)，所以结果出错。

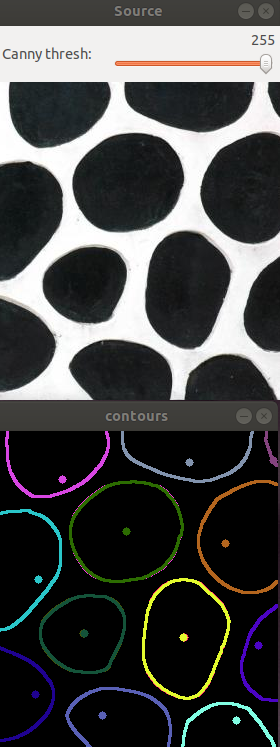
![20190130165133128.png][]![20190129221700963.png][]

质心：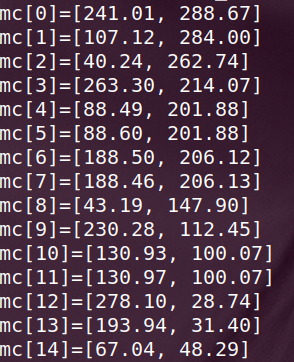  
![在这里插入图片描述][20190129221823257.png]

面积、长度：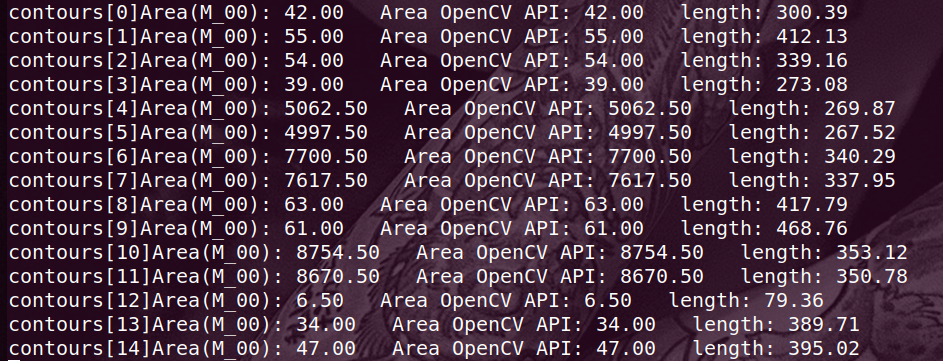  
![在这里插入图片描述][20190129221923766.png]分析：cv::moments函数，传入的是一组点，则算出的M00其实就是面积，和OpenCV API算出来的一样

--------------------

## OpenCV API ##

1.  计算图像的矩(最高到三阶)

[Moments cv::moments][Moments cv_moments]

( 	    InputArray  	array,     //single-channel, 8-bit or floating-point 2D array 或者 an array ( 1×N or N×1 ) of 2D points (Point or Point2f )，图像的话，以像素为基础，比如计算M00:所有像素之和； 点组成的多边形的话，计算M00等于面积，所以上面例子，M00和OpenCV api算出来一样面积结果
    		bool  	binaryImage = false  // 如果是true，非0图像像素即使1，此参数只针对图像而言
    )

返回  m o m e n t s moments moments 的成员变量：  
空间矩：m00、m01、 m02、m03、 m10、m11 、m12、m20、m21、m30  
中心矩：mu02、mu03、mu11、mu12、mu20、mu21、mu30  
归一化中心距：nu02、nu03、nu11、nu12、nu20、nu21、nu30

1.  通过上面得到的moments 得到hu矩

void cv::HuMoments

( 	    const Moments &  	moments, //由上面函数得到
    		double  	hu[7]  //得到7个不变矩
    )

1.  计算轮廓面积

[double cv::contourArea ][double cv_contourArea]

( 	    InputArray  	contour,  // 一组点（不是图像），可以存在vector<Point>或者Mat
    		bool  	oriented = false  // false：返回是面积绝对值，true: 返回面积有正负，这样通过正负来判断轮廓点的方向（顺时针、逆时针）
    )

1.  计算轮廓周长、弧的长度

[double cv::arcLength][double cv_arcLength]

( 	    InputArray  	curve,  // 一组点（不是图像），可以存在vector<Point>或者Mat
    		bool  	closed    // 点之间是否是closed
    ) 	
    
    （已经验证）比如： 三个点(0,0) ，(10,0)，(10,10); closed:true 结果是34.1421，closed:false结果是20

实例

vector<Point> contour; //创建一个由四个点组成的轮廓
    contour.push_back(Point(0,0));
    contour.push_back(Point(10,0));
    contour.push_back(Point(10,10));
    contour.push_back(Point(5,4));
    
    Mat src(2,2,CV_8UC1, 10); //创建一个2*2 的图像
    
    
    
    double area0 = contourArea(contour);  //计算四个点组成轮廓的面积
    cv::Moments moment1 = cv::moments(contour);// 计算轮廓的矩
    
    
    vector<Point> approx;
    approxPolyDP(contour, approx, 5, true);  //由轮廓近似得到 多边形 approx
    cv::Moments moment2 = cv::moments(approx); // 计算 approx的矩
    double area1 = contourArea(approx); // 计算 approx的面积
    
    cv::Moments moments3 = cv::moments(src); //计算Mat src的矩
    
    cout << "Mat src M00: " << moments3.m00 << endl; //输出src矩的m00 ，相当于所有像素之和
    cout << endl;
    
    cout << "contour M00: " << moment1.m00 << endl; //contour的矩m00，
    cout << "approx M00: " << moment2.m00 << endl;  //approx的矩m00，
    cout << endl;
    
    cout << "area of contourArea(contour): "<< area0 << endl; //ontourArea(contour)计算由四个点组成的面积
    cout << "area of contourArea(approx): "<< area1 << endl; //contourArea(approx)计算由三个点（由轮廓近似而得到）组成面积
    cout << "approx poly vertices： " << approx.size() << endl; //由轮廓contour四个点近似得到多边形approx的多少个点

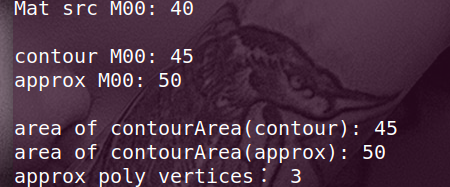
![在这里插入图片描述][20190130111133822.png]

分析： 可以看出，当cv::moments()传入的参数不同，结果不同，如果传入是：

1.  Mat src：二维图像，单通道8bit，则空间矩M00计算的是所有像素之和，
2.  contour 或者是approx：由点组成的多边形，M00计算的是由点组成的面积，且和contourArea函数计算结果一样

[20190130100028248.png]: /images/20220321/6132783c1c5445f4b5a3add742f3d031.png
[20190130165133128.png]: https://img-blog.csdnimg.cn/20190130165133128.png
[20190129221700963.png]: /images/20220321/fb6fc7d8db40421a82bca531fdaef845.png
[20190129221823257.png]: /images/20220321/938bcde3f9af47b99f643d15a2739cd3.png
[20190129221923766.png]: /images/20220321/587afce0b6474a199a9fd0ac004ff13c.png
[Moments cv_moments]: https://docs.opencv.org/master/d3/dc0/group__imgproc__shape.html#ga556a180f43cab22649c23ada36a8a139
[double cv_contourArea]: https://docs.opencv.org/master/d3/dc0/group__imgproc__shape.html#ga2c759ed9f497d4a618048a2f56dc97f1
[double cv_arcLength]: https://docs.opencv.org/master/d3/dc0/group__imgproc__shape.html#ga8d26483c636be6b35c3ec6335798a47c
[20190130111133822.png]: /images/20220321/34675e1785704c518691d36d6ccf05d5.png