图像得矩-蒲公英云

图像得矩

图像的矩

零阶矩： M00
这里的图像是单通道图像，表示图像在点上的灰度值。
我们可以发现，当图像为二值图时，就是这个图像上白色区域的总和，因此，可以用来求二值图像（轮廓，连通域）的面积。

一阶矩： M01 / M10
当图像为二值图时, 只有 0（黑），1（白）两个值。就是图像上所以白色区域 x 坐标值的累加。因此，一阶矩可以用来求二值图像的重心

二阶矩 M20 / M02 / M11
二阶矩可以用来求物体形状的方向。

几何矩公式

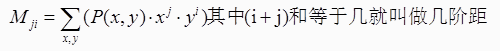
在这里插入图片描述

P(x,y) 表示 x，y 处的灰度值 x,y 表示图像二维中的坐标（i=0,j=0时表示零阶矩， i=1,j=0或i=0,j=1表示 1阶矩…….以此类推）

目前 opencv 支持求 0-3阶矩

利用矩求图像的重心，方向

Mat image = imread(imagename, 0);//读入灰度图
Mat binary;
//二值，椭圆是黑色的，所以反色下
threshold(image, binary, 200, 255, CV_THRESH_BINARY_INV);
Moments m = moments(binary, true);//moments()函数计算出三阶及一下的矩
Point2d center(m.m10 / m.m00, m.m01 / m.m00);//此为重心
//计算方向
double a = m.m20 / m.m00 - center.x*center.x;
double b = m.m11 / m.m00 - center.x*center.y;
double c = m.m02 / m.m00 - center.y*center.y;
double theta = fastAtan2(2*b,(a - c))/2;//此为形状的方向
//其中：fastAtan2()为OpenCV的函数，输入向量，返回一个0-360的角度。

20160331211012268

矩的计算及特性

opencv Momets 数据结构

class Moments
{
public:
    Moments();
    Moments(double m00, double m10, double m01, double m20, double m11,
            double m02, double m30, double m21, double m12, double m03 );
    Moments( const CvMoments& moments );
    operator CvMoments() const;
    // spatial moments空间矩
    double  m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;
    // central moments中心矩
    double  mu20, mu11, mu02, mu30, mu21, mu12, mu03;
    // central normalized moments归一化的中心矩
    double  nu20, nu11, nu02, nu30, nu21, nu12, nu03;
}

2.1空间矩（0-3阶）

空间矩的实质为面积或者质量。可以通过一阶矩计算质心/重心。

watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTE4MDg2NzM_size_16_color_FFFFFF_t_70

2.2中心矩（0-3阶）

中心矩体现的是图像强度的最大和最小方向（中心矩可以构建图像的协方差矩阵），其只具有平移不变性，所以用中心矩做匹配效果不会很好。

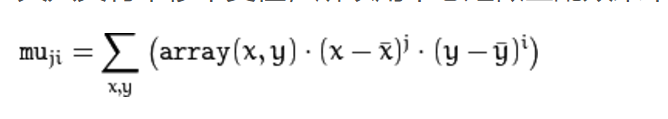
2.3归一化的中心矩（0-3阶）

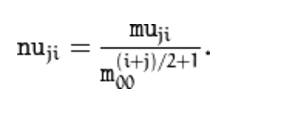
归一化后具有了平移和尺度不变性。

2.4 Hu矩Hu矩由于具有尺度、旋转、平移不变性，可以用来做匹配。
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTE4MDg2NzM_size_16_color_FFFFFF_t_70 1

opencv hu_moments() 获取图像的 Hu 矩

小结

图像的矩通常描述了该图像形状的全局特征，并被广泛的应用在各种图像处理、计算机视觉和机器人技术领域的目标识别与方位估计中。一阶矩与形状有关，二阶矩显示曲线围绕直线平均值的扩展程度，三阶矩则是关于平均值的对称性的测量。不变矩是图像的统计特性，满足平移、伸缩、旋转均不变的不变性。
如果把图像看成是一块质量密度不均匀的薄板，其图像的灰度分布函数f(x,y)就是薄板的密度分布函数，则其各阶矩有着不同的含义，如零阶矩表示它的总质量；一阶矩表示它的质心；二阶矩又叫惯性矩，表示图像的大小和方向。事实上，如果仅考虑阶次为2的矩集，则原始图像等同于一个具有确定的大小、方向和离心率，以图像质心为中心且具有恒定辐射率的椭圆。
由三阶矩以下矩构成的七个矩不变量具有平移、旋转和尺度不变性等等。当密度分布函数发生改变时，图像的实质没有改变，仍然可以看做一个薄板，只是密度分布有所改变。虽然此时各阶矩的值可能发生变化，但由各阶矩计算出的不变矩仍具有平移、旋转和尺度不变性。通过这个思想，可对图像进行简化处理，保留最能反映目标特性的信息，再用简化后的图像计算不变矩特征，可减少计算量。
研究表明，只有基于二阶矩的不变矩对二维物体的描述才是真正的与旋转、平移和尺度无关的。较高阶的矩对于成像过程中的误差，微小的变形等因素非常敏感，所以相应的不变矩基本上不能用于有效的物体识别。即使是基于二阶矩的不变矩也只能用来识别外形相差特别大的物理，否则他们的不变矩会因为很相似而不能识别