JS实现图的深度优先遍历(DFS)和广度优先遍历(BFS)
1 建立测试图(邻接矩阵和邻接表存储形式)
首先建立一个图用于后续代码的测试,在此以无向图为例,且所有边的权值都为1。存储方式分别为邻接矩阵和邻接表(见上一篇介绍)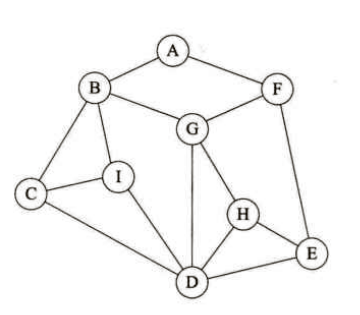
邻接矩阵:
class Graph{constructor(v,vr){let len = v.lengththis.vexs = [].slice.apply(v);let arcs = [];for (let i=0;i<len;i++){arcs[i] = new Array(len);for (let j=0;j<len;j++){arcs[i][j] = i===j ? 0 : 65535;}}for (let arc of vr){let v1 = v.indexOf(arc[0]);let v2 = v.indexOf(arc[1]);arcs[v1][v2] = arcs[v2][v1] = arc[2] || 1;}this.arcs = arcs;}}let a = new Graph(['A','B','C','D','E','F','G','H','I'],[['A','B',1],['A','F',1],['B','G',1],['F','G',1],['B','C',1],['B','I',1],['G','H',1],['C','I',1],['I','D',1],['H','D',1],['F','E',1],['H','E',1],['C','D',1]]);console.log(a);
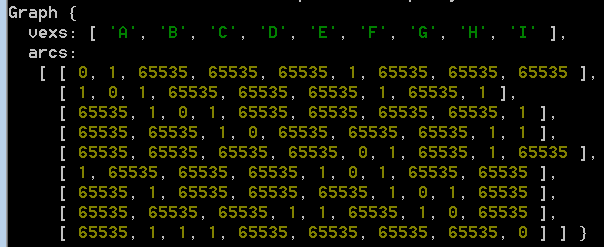
邻接表:
class vex{constructor(value){this.data = value;this.firstEdge = null;}}class adjvex{constructor(node,weight){this.node = node;this.weight = weight;this.next = null;}}class Graph{constructor(v,vr){let len = v.length;let vexs = new Array(len);let v1=0,v2=0;let newvex = null;for (let i=0;i<len;i++){vexs[i] = new vex(v[i]);}for (let arc of vr){v1 = v.indexOf(arc[0]);v2 = v.indexOf(arc[1]);newvex = new adjvex(v1,arc[2]);newvex.next = vexs[v2].firstEdge;vexs[v2].firstEdge = newvex;newvex = new adjvex(v2,arc[2]);newvex.next = vexs[v1].firstEdge;vexs[v1].firstEdge = newvex;}this.adjList = vexs;}}let a = new Graph(['A','B','C','D','E','F','G','H','I'],[['A','B',1],['A','F',1],['B','G',1],['F','G',1],['B','C',1],['B','I',1],['G','H',1],['C','I',1],['I','D',1],['H','D',1],['F','E',1],['H','E',1],['C','D',1]]);console.log(a);
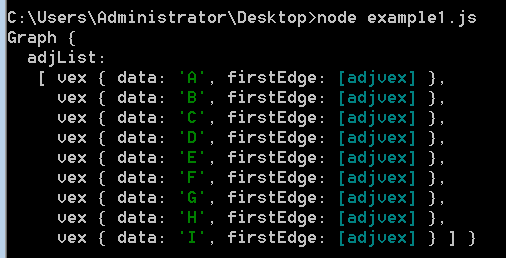
2 深度优先遍历
深度优先遍历是一个递归过程,其从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发,深度优先遍历图,直至图中所有点都被访问到,类似于树的前序遍历。
邻接矩阵:
function DFSTraverse(G){let visited = new Array(G.vexs.length); //用于标记顶点是否被访问过for (let i=0;i<G.vexs.length;i++){ //初始化visited[i] = false;}for (let i=0;i<G.vexs.length;i++){ //从第一个点开始递归访问if (visited[i] === false){visited[i] = true;DFS(i);}}function DFS(i){console.log(G.vexs[i]);for (let j=0;j<G.vexs.length;j++){if (G.arcs[i][j] === 1 && visited[j] === false){ //访问未访问过的邻接点visited[j] = true;DFS(j);}}}}

邻接表:
function DFSTraverse(G){let visited = new Array(G.adjList.length); //用于标记顶点是否被访问过for (let i=0;i<G.adjList.length;i++){ //初始化visited[i] = false;}for (let i=0;i<G.adjList.length;i++){ //从第一个点开始递归访问if (visited[i] === false){visited[i] = true;DFS(i);}}function DFS(i){console.log(G.adjList[i].data);let adjvex = G.adjList[i].firstEdge;while(adjvex){if (visited[adjvex.node] === false){ //访问未访问过的邻接点visited[adjvex.node] = true;DFS(adjvex.node);}adjvex = adjvex.next;}}}
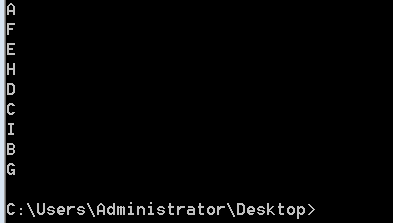
3 广度优先遍历
广度优先遍历类似于树的层序遍历,其从图中某顶点v出发,访问了v之后一次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,且先被访问的顶点的邻接点先于后被访问的顶点的邻接点,直至图中所有顶点都被访问。
邻接矩阵:
function BFSTraverse(G){let queue = []; //使用队列进行层序遍历let visited = new Array(G.vexs.length);let vexnum = 0;for (let i=0;i<G.vexs.length;i++){visited[i] = false;}for (let i=0;i<G.vexs.length;i++){if (visited[i] === false){visited[i] = true;queue.push(i);while(queue.length > 0){vexnum = queue.shift(); //弹出队列头部序号,并访问节点console.log(G.vexs[vexnum]);for (let j=0;j<G.vexs.length;j++){ //将当前节点未访问过的的邻接点序号推入队列if (G.arcs[vexnum][j] === 1 && visited[j] === false){visited[j] = true;queue.push(j);}}}}}}
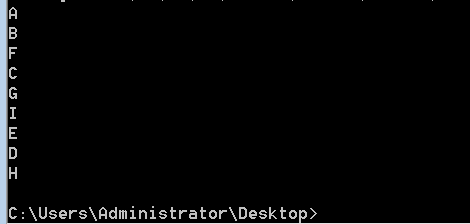
邻接表:
function BFSTraverse(G){let queue = [];let visited = new Array(G.adjList.length);let vexnum = 0;let adjvex = null;for (let i=0;i<G.adjList.length;i++){visited[i] = false;}for (let i=0;i<G.adjList.length;i++){if (visited[i] === false){visited[i] = true;queue.push(i);}while(queue.length > 0){vexnum = queue.shift(); //弹出队列头部序号,并访问节点console.log(G.adjList[vexnum].data);adjvex = G.adjList[vexnum].firstEdge;while(adjvex){ //将当前节点未访问过的的邻接点序号推入队列if (visited[adjvex.node] === false){visited[adjvex.node] = true;queue.push(adjvex.node);}adjvex = adjvex.next;}}}}
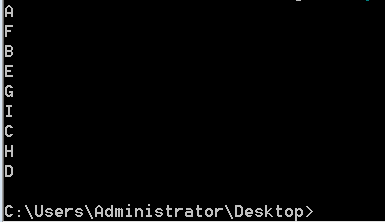
如果觉得这篇文章帮助了您,请打赏一个小红包鼓励作者继续创作哦!!!
































还没有评论,来说两句吧...