(C/C++)-图的深度优先遍历(DFS)和广度优先遍历(BFS)
(C/C++)-图的深度优先遍历(DFS)和广度优先遍历(BFS)
1、图的深度优先遍历(DFS)
图的深度优先遍历与树的先序遍历类似,即尽可能深的遍历图
这里采取邻接矩阵存储图,存储的图如下:
ps: 这个图沿用我的上一篇文章(最小生成树和单源最短路径),有兴趣的伙伴可以看看——点击传送门
基本思想:
- 先访问图的某一顶点v,然后由顶点v出发,访问与顶点v邻接并且未被访问的任一顶点w1;
- 在由w1出发,访问与顶点w1邻接并且未被访问的任一顶点w2;
- 重复上述过程,直到所有顶点被访问;
具体实现:
图遍历所需的基本函数:
int visited[N] = {0};//标记顶点是否被访问,初始为0int s[N] = {0 };//标记顶点是否被访问,初始为0(NextNeighbor():这里用辅助数组s[i],防止无限套娃-_-)//返回图G中顶点v的一个邻接顶点,若不存在则返回-1int FirstNeighbor(int G[N][N], int v){int i;for (i = 1; i < N; i++)if (G[v][i] != maxint)return i;return -1;}//返回图G中顶点v的一个不是w的邻接顶点,若不存在则返回-1int NextNeighbor(int G[N][N], int v, int w){int i;for (i = 1; i < N; i++)if (G[v][i] != maxint && i != w && !s[i])//这里用辅助数组s[i],防止无限套娃-_-{s[i] = 1;return i;}return -1;}
深度优先遍历过程:
//从顶点v开始做深度优先遍历void DFS(int G[N][N], int v){printf("%d ", v);//先访问顶点vvisited[v] = 1;//标记顶点v已经访问//深度优先遍历for (int w = FirstNeighbor(G, v); w >= 1; w = NextNeighbor(G, v, w))if (!visited[w])DFS(G, w);}//从每个顶点进行深度优先遍历,防止非连通图void DFSTraverse(int G[N][N]){for (int v = 1; v < N; v++)if (!visited[v])DFS(G, v);}
接下来在main()函数中测试一下
int main(){int G[N][N] = {{0},//0号下标不使用{0,maxint,10,maxint,maxint,5},{0,maxint,maxint,1,maxint,2},{0,maxint,maxint,maxint,4,maxint},{0,7,maxint,6,maxint,maxint},{0,maxint,3,9,2,maxint}};//5个顶点,0号下标不使用DFSTraverse(G);return 0;}
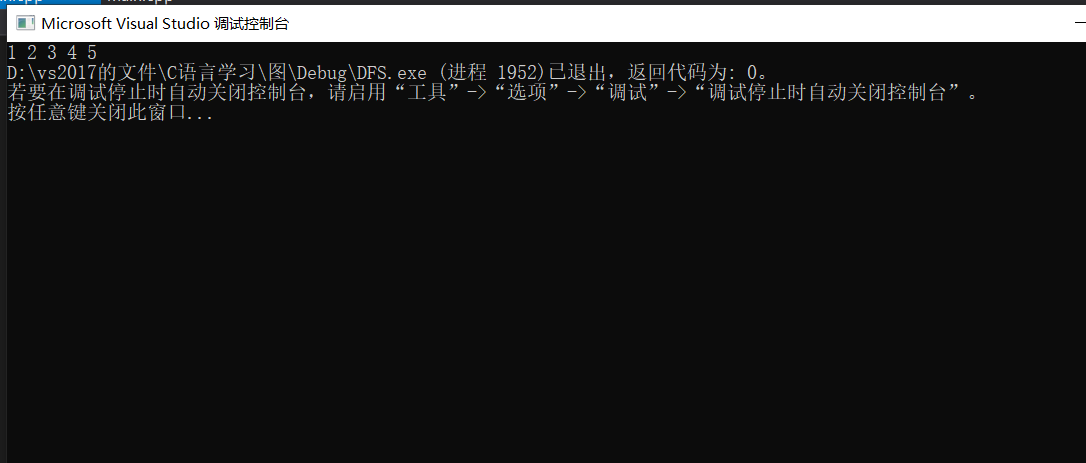
2、图的广度优先遍历(BFS)
图的广度优先遍历与树的层次遍历类似,需要借助队列来实现
ps:沿用上图
基本思想:
- 首先访问某一顶点v,并由v出发,依次访问顶点v未被访问过的所有邻接顶点w1,w2…wi;
- 再依次访问w1,w2…wi未被访问过的所有邻接顶点;
- 重复上述过程,直到所有顶点被访问;
具体实现:
//从顶点v开始做广度优先遍历void BFS(int G[N][N], int v){printf("%d ", v);//访问顶点vvisited[v] = 1;//标记顶点v已经访问//广度优先遍历(类似二叉树层次遍历)que.push(v);while (!que.empty()){v = que.front();que.pop();//出队for (int w = FirstNeighbor(G, v); w >= 1; w = NextNeighbor(G, v, w))if (!visited[w]){printf("%d ", w);//访问顶点wvisited[w] = 1;que.push(w);}}}//从每个顶点进行广度优先遍历,防止非连通图void BFSTraverse(int G[N][N]){for (int v = 1; v < N; v++)if (!visited[v])BFS(G, v);}
在main()中测试:
int main(){int G[N][N] = {{0},//0号下标不使用{0,maxint,10,maxint,maxint,5},{0,maxint,maxint,1,maxint,2},{0,maxint,maxint,maxint,4,maxint},{0,7,maxint,6,maxint,maxint},{0,maxint,3,9,2,maxint}};//5个顶点,0号下标不使用BFSTraverse(G);return 0;}
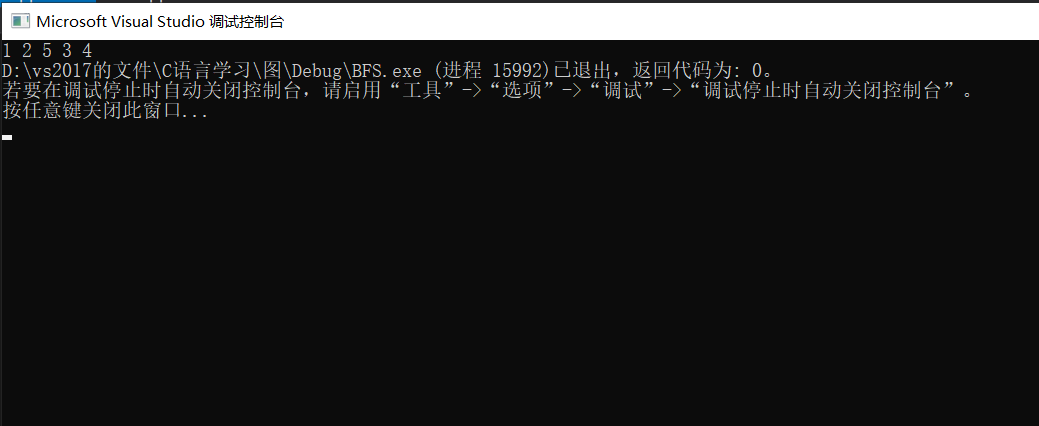
图的两种遍历方式学习到这里就结束了:)





























还没有评论,来说两句吧...