运动学模型

三轮全向轮小车结构示意图如图所示：

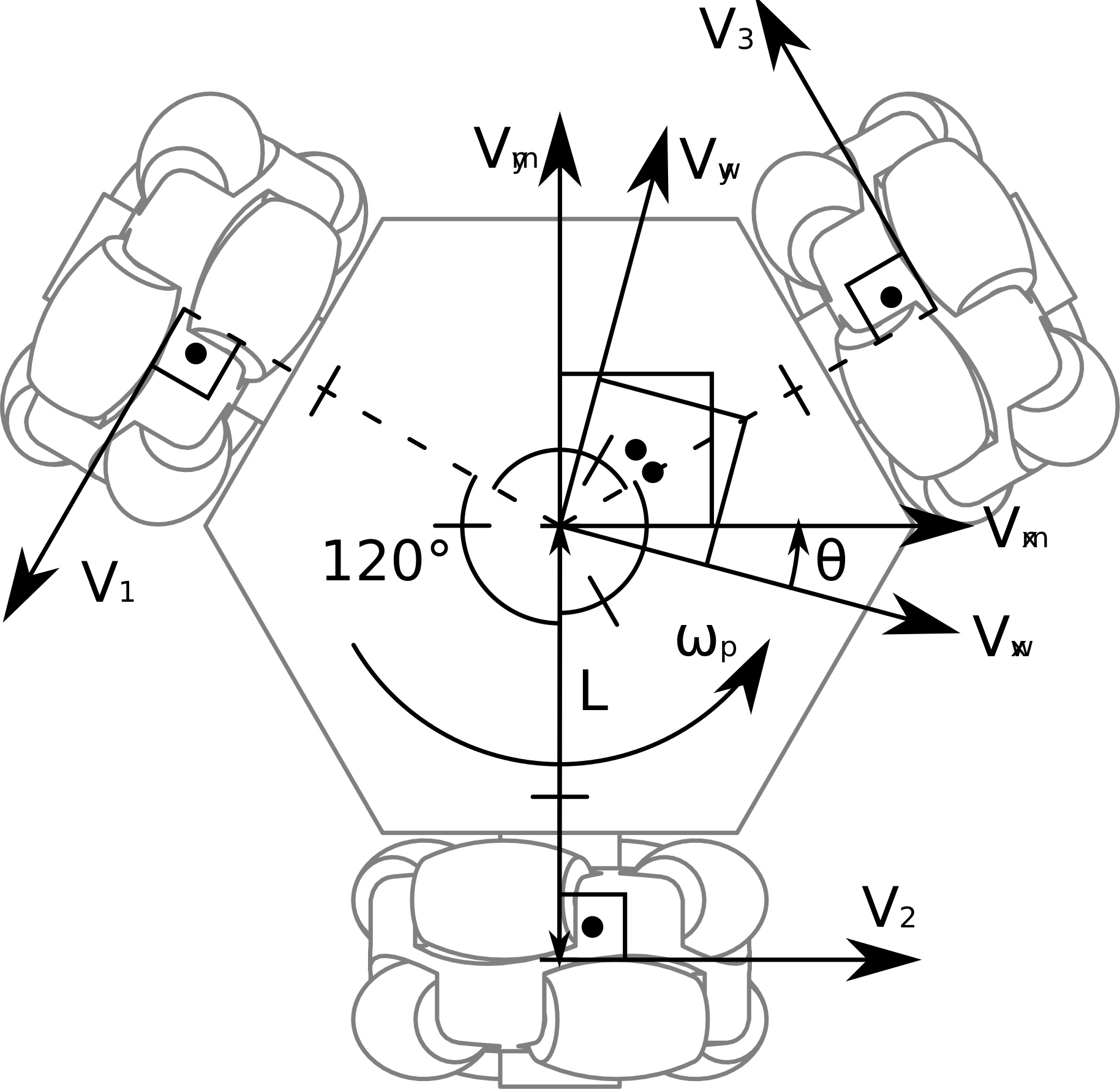
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzE2Nzc1Mjkz_size_16_color_FFFFFF_t_70

图中V1，V2和V3也分别称为V_left，V_back和V_right，对应三个轮子的转速，转动的正方向如图所示。

小车坐标系下运动模型分析

V x m = 2 V 2 − V 1 − V 3 3 {V}_x^m=\frac{2V_2-V_1-V3}{3} Vxm=32V2−V1−V3
V y m = 3 V 3 − 3 V 1 3 {V}_y^m=\frac{\sqrt{3}V_3-\sqrt{3}V_1}{3} Vym=33V3−3V1
ω p = V 1 + V 2 + V 3 3 L {\omega}_p=\frac{V_1+V_2+V_3}{3L} ωp=3LV1+V2+V3

对应C语言代码如下：

bool forwardMobile(smart_car::KinematicsForward::Request &request, smart_car::KinematicsForward::Response &response) { 
    response.output.x     = ((2.0L * request.input.v_back) - request.input.v_left - request.input.v_right) / 3.0L;
    response.output.y     = ((sqrt3 * request.input.v_right) - (sqrt3 * request.input.v_left)) / 3.0L;
    response.output.theta = (request.input.v_left + request.input.v_back + request.input.v_right) / L3;
    return true;
}

小车坐标系与世界坐标系转换

小车坐标系转换到世界坐标系

小车坐标系转换到世界坐标系的公式如下：

V x w = cos ⁡ ( θ ) V x m − sin ⁡ ( θ ) V y m {V}_x^w=\cos(\theta)V_x^m-\sin(\theta)V_y^m Vxw=cos(θ)Vxm−sin(θ)Vym
V y w = sin ⁡ ( θ ) V x m + cos ⁡ ( θ ) V y m {V}_y^w=\sin(\theta)V_x^m+\cos(\theta)V_y^m Vyw=sin(θ)Vxm+cos(θ)Vym

其中 V x w {V}_x^w Vxw与 V y w {V}_y^w Vyw分别代表世界坐标系下 x x x与 y y y轴的方向， V x m {V}_x^m Vxm与 V y m {V}_y^m Vym分别代表小车坐标系下 x x x与 y y y轴的方向。

对应c语言代码如下：

void mobileToWorldCore(double Vxm, double Vym, double& Vxw, double& Vyw) { 
    Vxw = (std::cos(theta) * Vxm) - (std::sin(theta) * Vym);
    Vyw = (std::sin(theta) * Vxm) + (std::cos(theta) * Vym);
}

世界坐标系转换到小车坐标系

同理，小车坐标系转换到小车坐标系的公式如下：

V x m = cos ⁡ ( θ ) V x w + sin ⁡ ( θ ) V y w {V}_x^m=\cos(\theta)V_x^w+\sin(\theta)V_y^w Vxm=cos(θ)Vxw+sin(θ)Vyw
V y m = − sin ⁡ ( θ ) V x w + cos ⁡ ( θ ) V y w {V}_y^m=-\sin(\theta)V_x^w+\cos(\theta)V_y^w Vym=−sin(θ)Vxw+cos(θ)Vyw

对应c语言代码如下：

void worldToMobileCore(double Vxw, double Vyw, double& Vxm, double& Vym) { 
    Vxm =   (std::cos(theta) * Vxw) + (std::sin(theta) * Vyw);
    Vym = - (std::sin(theta) * Vxw) + (std::cos(theta) * Vyw);
}

小车运动与电机转动对应关系

V 1 = − V x m 2 − 3 V y m 2 + L ω p {V}_1=-\frac{V_x^m}{2}-\frac{\sqrt{3}V_y^m}{2}+L\omega_p V1=−2Vxm−23Vym+Lωp
V 2 = V x m + L ω p {V}_2=V_x^m+L\omega_p V2=Vxm+Lωp
V 3 = − V x m 2 + 3 V y m 2 + L ω p {V}_3=-\frac{V_x^m}{2}+\frac{\sqrt{3}V_y^m}{2}+L\omega_p V3=−2Vxm+23Vym+Lωp

对应C语言代码为：

bool inverseMobile(smart_car::KinematicsInverse::Request &request, smart_car::KinematicsInverse::Response &response) { 
    long double V__m_x2 = - request.input.x / 2.0L;
    long double sqrt3V__m_y2 = (sqrt3 * request.input.y) / 2.0L;
    long double Lomega_p = L * request.input.theta;
    response.output.v_left  = V__m_x2 - sqrt3V__m_y2 + Lomega_p;
    response.output.v_back  = request.input.x        + Lomega_p;
    response.output.v_right = V__m_x2 + sqrt3V__m_y2 + Lomega_p;
    return true;

完整代码

#include <cmath>
#include <string>
#include <ros/ros.h>
#include <geometry_msgs/Pose2D.h>
#include <sensor_msgs/JointState.h>
#include <smart_car/FrameToFrame.h>
#include <smart_car/KinematicsForward.h>
#include <smart_car/KinematicsInverse.h>
#include <kdl/frames.hpp>
#include <kdl_parser/kdl_parser.hpp>
long double L;
long double L3;
long double sqrt3;
long double theta = 0;
void mobileToWorldCore(double Vxm, double Vym, double& Vxw, double& Vyw) { 
    Vxw = (std::cos(theta) * Vxm) - (std::sin(theta) * Vym);
    Vyw = (std::sin(theta) * Vxm) + (std::cos(theta) * Vym);
}
bool mobileToWorld(smart_car::FrameToFrame::Request &request, smart_car::FrameToFrame::Response &response) { 
    mobileToWorldCore(request.input.x, request.input.y, response.output.x, response.output.y);
}
void worldToMobileCore(double Vxw, double Vyw, double& Vxm, double& Vym) { 
    Vxm =   (std::cos(theta) * Vxw) + (std::sin(theta) * Vyw);
    Vym = - (std::sin(theta) * Vxw) + (std::cos(theta) * Vyw);
}
bool worldToMobile(smart_car::FrameToFrame::Request &request, smart_car::FrameToFrame::Response &response) { 
    worldToMobileCore(request.input.x, request.input.y, response.output.x, response.output.y);
}
bool forwardMobile(smart_car::KinematicsForward::Request &request, smart_car::KinematicsForward::Response &response) { 
    response.output.x     = ((2.0L * request.input.v_back) - request.input.v_left - request.input.v_right) / 3.0L;
    response.output.y     = ((sqrt3 * request.input.v_right) - (sqrt3 * request.input.v_left)) / 3.0L;
    response.output.theta = (request.input.v_left + request.input.v_back + request.input.v_right) / L3;
    return true;
}
bool forwardWorld(smart_car::KinematicsForward::Request &request, smart_car::KinematicsForward::Response &response) { 
    forwardMobile(request, response);
    mobileToWorldCore(response.output.x, response.output.y, response.output.x, response.output.y);
    return true;
}
bool inverseMobile(smart_car::KinematicsInverse::Request &request, smart_car::KinematicsInverse::Response &response) { 
    long double V__m_x2 = - request.input.x / 2.0L;
    long double sqrt3V__m_y2 = (sqrt3 * request.input.y) / 2.0L;
    long double Lomega_p = L * request.input.theta;
    response.output.v_left  = V__m_x2 - sqrt3V__m_y2 + Lomega_p;
    response.output.v_back  = request.input.x        + Lomega_p;
    response.output.v_right = V__m_x2 + sqrt3V__m_y2 + Lomega_p;
    return true;
}
bool inverseWorld(smart_car::KinematicsInverse::Request &request, smart_car::KinematicsInverse::Response &response) { 
    worldToMobileCore(request.input.x, request.input.y, request.input.x, request.input.y);
    inverseMobile(request, response);
    return true;
}
void onPoseWorldMessage(const geometry_msgs::Pose2D::ConstPtr& input){ 
    theta = input->theta;
}
int main(int argc, char **argv){ 
    ros::init(argc, argv, "kinematics");
    ros::NodeHandle node;
    { 
        std::string description;
        if(!node.getParam("robot_description",description)) { 
            ROS_ERROR("Could not find '/robot_description'.");
            return -1;
        }
        KDL::Tree tree;
        if (!kdl_parser::treeFromString(description, tree)) { 
            ROS_ERROR("Failed to construct KDL tree.");
            return -1;
        }
        KDL::Chain chain;
        if (!tree.getChain("base_link", "rim_back_link", chain)) { 
            ROS_ERROR("Failed to get chain from KDL tree.");
            return -1;
        }
        KDL::Frame frame = chain.getSegment(0).pose(0);
        L = std::sqrt(std::pow(frame.p.x() - 0.0L, 2.0L) + std::pow(frame.p.y() - 0.0L, 2.0L));
        node.setParam("parameter/wheel/distance", (double) L);
        L3 = 3.0L * L;
        sqrt3 = std::sqrt(3.0L);
        double parameter;
        if (!node.getParam("parameter/initial/theta", parameter)) { 
            parameter = 0;
        }
        theta = parameter;
    }
    ros::ServiceServer forwardMobileService = node.advertiseService("kinematics_forward_mobile", forwardMobile);
    ros::ServiceServer forwardWorldService  = node.advertiseService("kinematics_forward_world" , forwardWorld );
    ros::ServiceServer inverseMobileService = node.advertiseService("kinematics_inverse_mobile", inverseMobile);
    ros::ServiceServer inverseWorldService  = node.advertiseService("kinematics_inverse_world" , inverseWorld );
    ros::ServiceServer mobileToWorldService = node.advertiseService("kinematics_mobile_to_world" , mobileToWorld);
    ros::ServiceServer worldToMobileService = node.advertiseService("kinematics_world_to_mobile" , worldToMobile);
    ros::Subscriber subscriber = node.subscribe("pose/world", 1, onPoseWorldMessage);
    ros::spin();
    return 0;
}