最短路径—Floyd算法-蒲公英云

最短路径—Floyd算法

冷不防 2022-05-12 05:50 424阅读 0赞

Floyd算法：

1，从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。

2，对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。

Floyd-Warshall——只有五行的算法

求任意两个点之间的最短路程。从i号顶点到j号顶点只经过前k号顶点的最短路程，这是一种动态规划的思想。

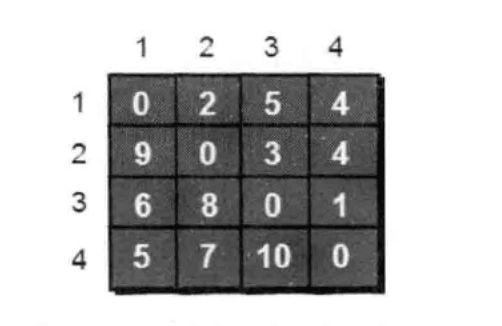
20170804221854439 20170804222015725

算法作为三个嵌套for循环。

for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];

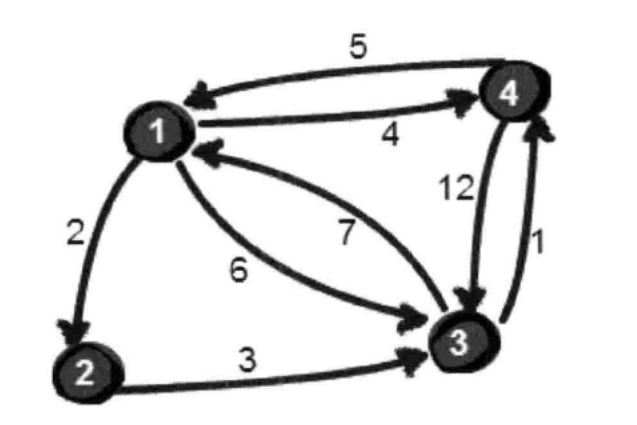
n个顶点，m条边，接下来的m行每一行有3个数，顶点u，v以及他们之间的距离 l。

#include<iostream>
using namespace std;
int e[111][111];
int n,m,u,v,l;
const int inf=999999;
void init()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i==j)
            e[i][j]=0;
            else
            e[i][j]=inf;
        }
    }
}
void floyd()
{
    int i,j,k;
    for(k=1;k<=n;k++)
    {
        for(i=1;i<=n;i++)
        {
            for(j=1;j<=n;j++)
            {
                if(e[i][k]<inf&&e[k][j]<inf&&e[i][j]>e[i][k]+e[k][j])
                e[i][j]=e[i][k]+e[k][j];
            }
        }
    }
}
int main()
{
    int i,j;
    cin>>n>>m;
    init();
    //读入边 
    for(i=1;i<=m;i++)
    {
        cin>>u>>v>>l;
        e[u][v]=l;
    }
    floyd();
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=n;j++)
        {
            cout<<e[i][j]<<endl;
        }
    }
    return 0;
}