最短路径——Dijkstra算法 & Floyd算法
从单个点到其余各点之间的最短路径——Dijkstra算法
各点之间的最短路径——Floyd算法
从单个点到其余各点间的最短路径**——Dijkstra**算法
基本思想
按照最短路径长度不减的次序求各顶点的解。若已知道路v0v1v2v3…vn-1vn是v0到vn最近的路,则途经的某顶点vi也为v0到vi最短的路。
方法如下:
(其中:path[v]和dist[v]表示从v0到v的最短路径及其长度)
(1)对v0以外的各顶点vi,若
(2)从未解顶点中选择一个dist值最小的顶点v,则当前的path[v]和dist[v]就是顶点v的最终解。
(3)由于某些顶点经过v可能会使得从v0到该顶点的路径更近一些,因此,应修改这些顶点的路径及其长度的值。
(4)重复(2)(3),直到所有顶点求解完毕。
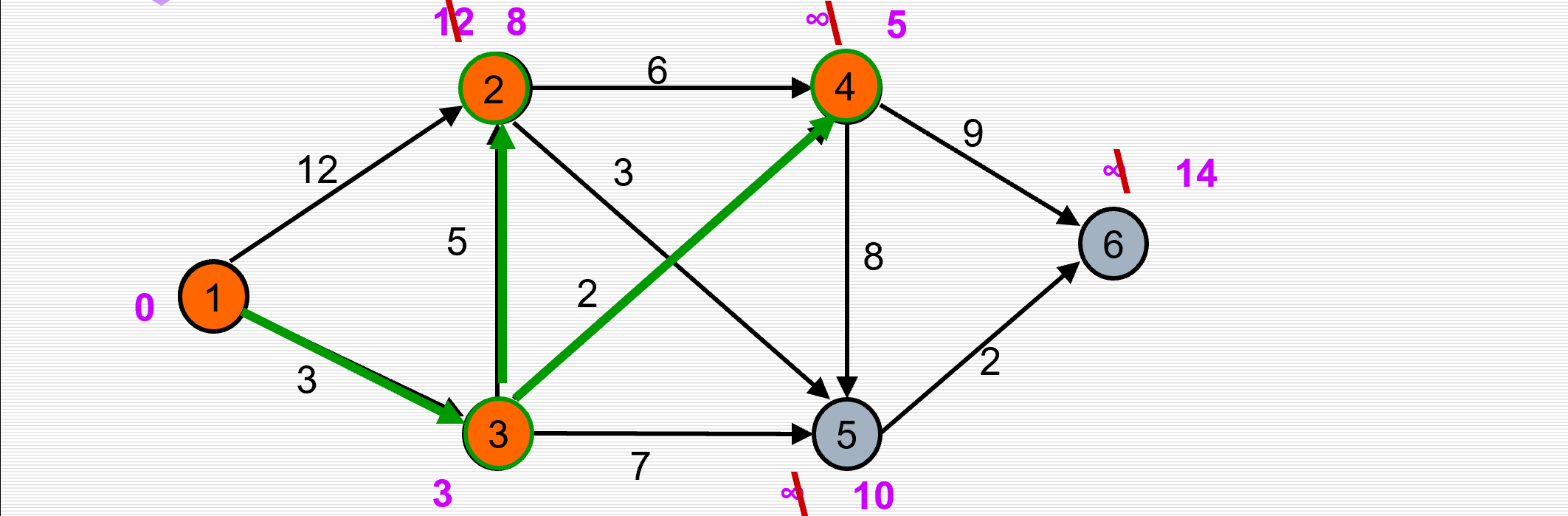
例子:求下图中顶点1到其余各顶点的最短路径。
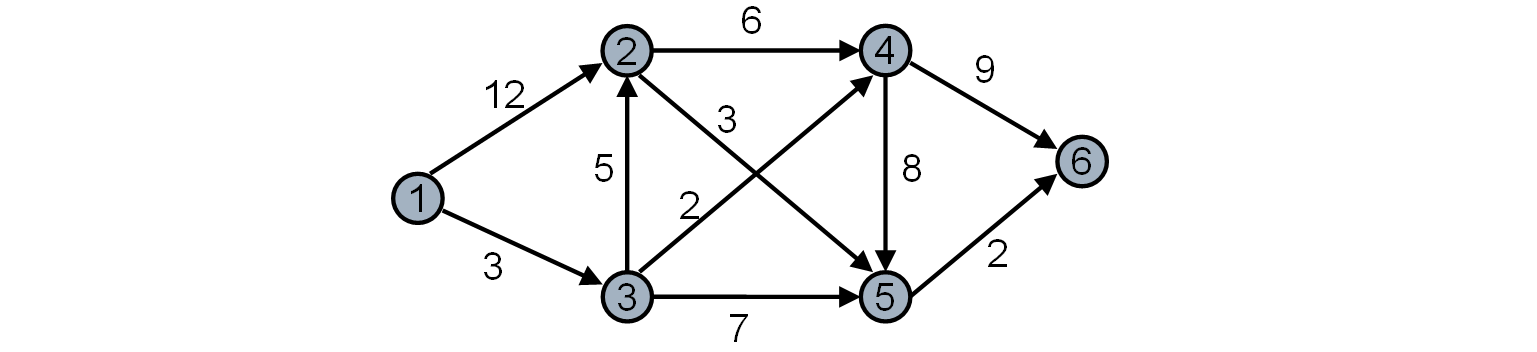
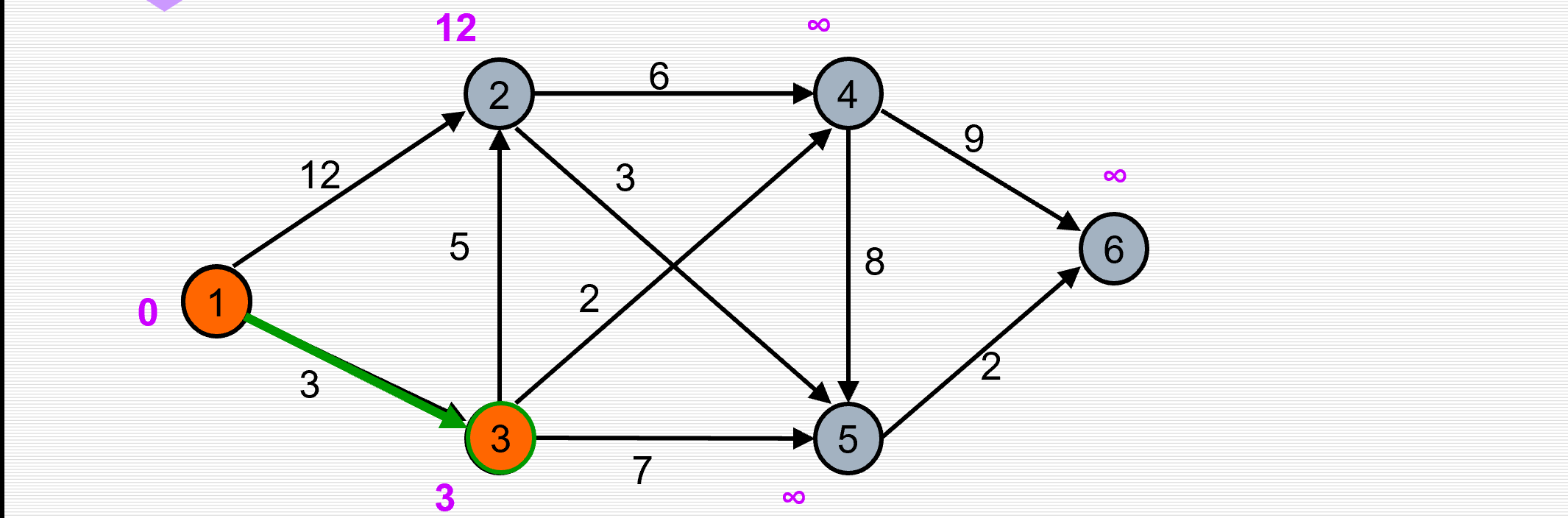
(1)初始化:1到v,若有边,则path[v]=边;dist[i]=边的值

(2)选出dist[i]为最小值,则path[i]为1到i的最短路径
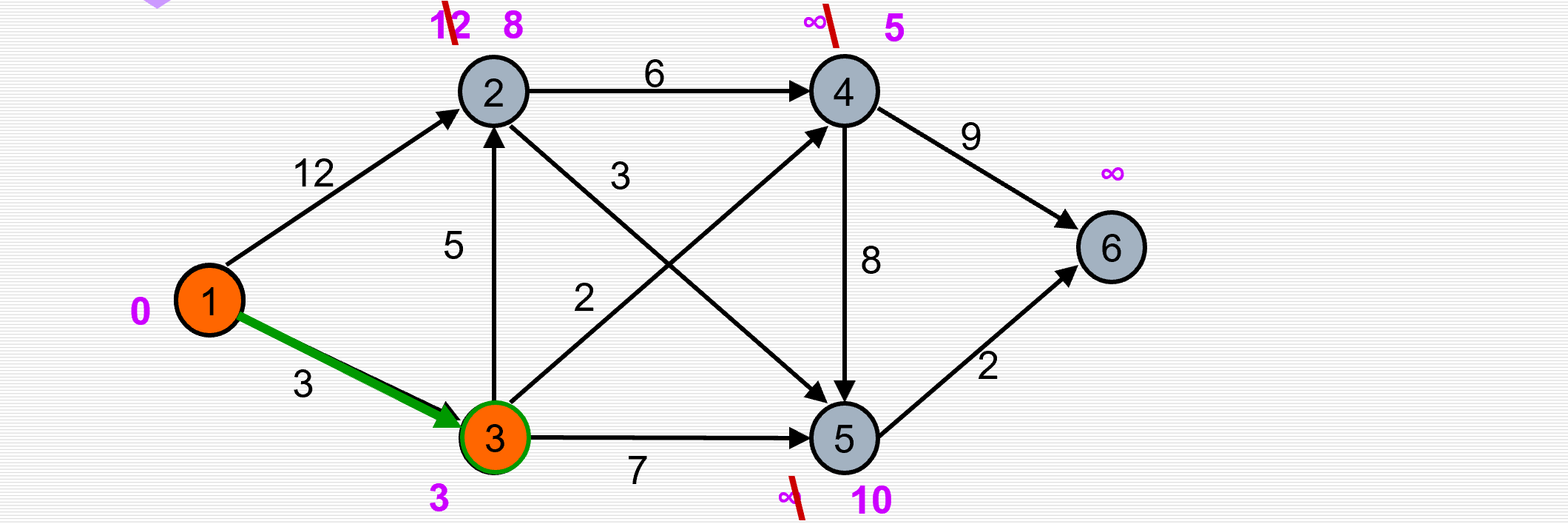
(3)修改经过i更近的路径
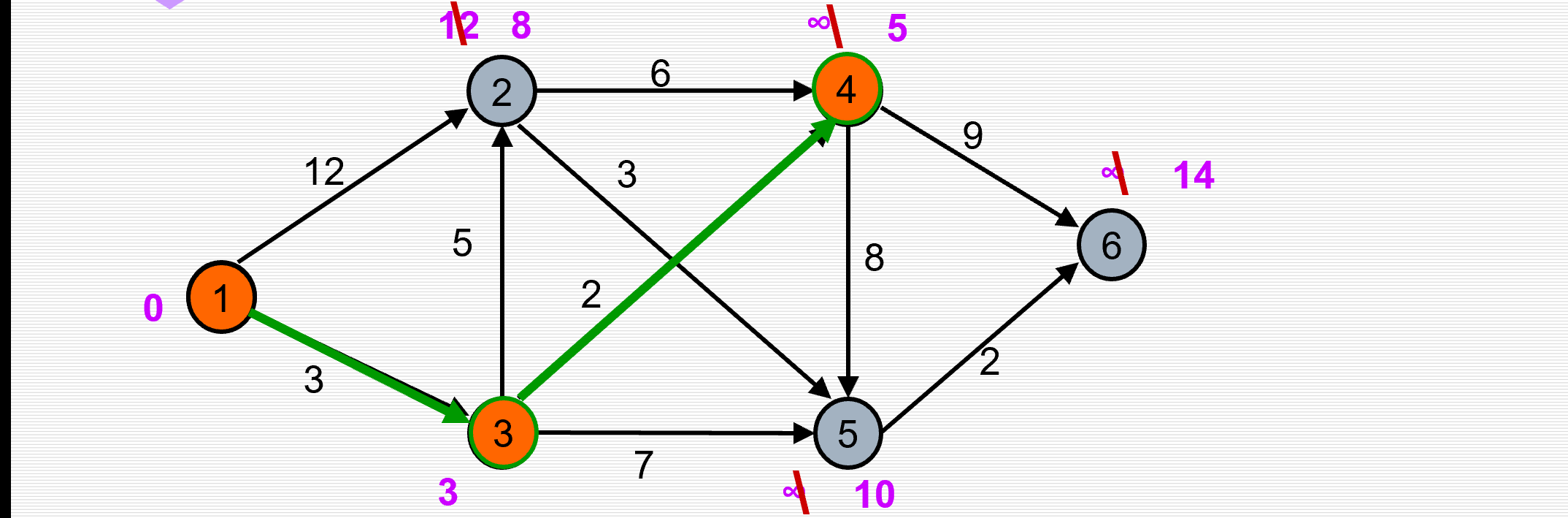
(4)重复(2)(3)……
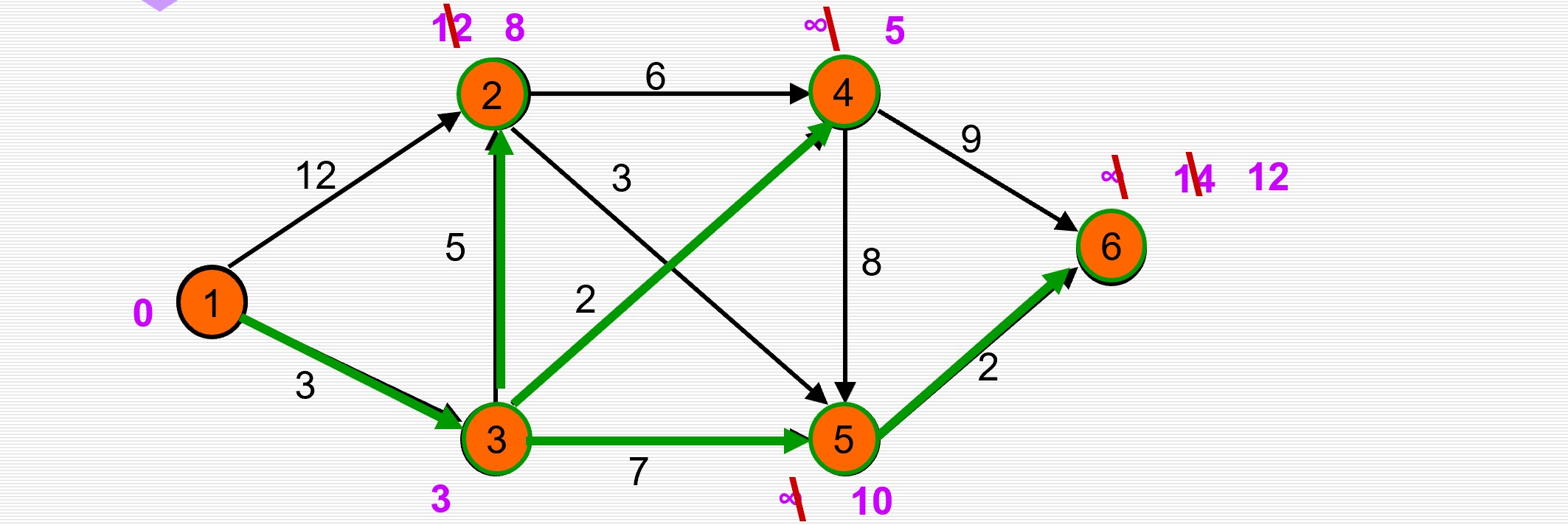
图采用邻接矩阵或邻接表来存储,算法复杂度均为O ( ) 。
各点间的最短路径**—— Floyd**算法
基本思想
通过矩阵序列实现A(0),A(1),…,A(n),其中A(k)中的元素A(k) [i,j]代表:顶点i到顶点j的当中间经过的顶点号不大于k时的最短路径长度。
如何求解各矩阵?
Floyd**算法采用的是由**A(k-1) 矩阵求A(k)的方法来实现的。
由A(k-1) 矩阵求A(k)的方法
可通过求得矩阵中的各元素A(k)ij来实现求解A(k)ij的求解:可**由**A(k-1) 矩阵中的相关元素来求得:

分两种情况讨论:
经过顶点k时,路径更短,
即A (k-1) ik \+ A (k-1) kj < A (k-1) ij ,则A (k) ij= A (k-1) ik \+ A (k-1) kj
经过顶点k时,路径更长,
即A (k-1) ik \+ A (k-1) kj >A (k-1) ij则A (k) ij =A (k-1)ij

依次选择编号为1的点为中间点(如【2,3】=【2,1】+【1,3】=4+3=7)得到,选择编号为2的点为中间点得到
,选择编号为3的点为中间点得到
,选择编号为4的点为中间点得到
。
算法复杂度为O() .
































还没有评论,来说两句吧...