已知二叉树的前序遍历和中序遍历，如何得到它的后序遍历？

曾经终败给现在 2022-05-24 05:10 135阅读 0赞

对一棵二叉树进行遍历，我们可以采取3中顺序进行遍历，分别是前序遍历、中序遍历和后序遍历。这三种方式是以访问父节点的顺序来进行命名的。假设父节点是N，左节点是L，右节点是R，那么对应的访问遍历顺序如下：

前序遍历 N－>L－>R  
中序遍历 L－>N－>R  
后序遍历 L－>R－>N  
/***\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\****/  
声明：本博内容均由[http://blog.csdn.net/droidphone][http_blog.csdn.net_droidphone]原创，转载请注明出处，谢谢！  
/***\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\*\****/

所以，对于以下这棵树，三种遍历方式的结果是：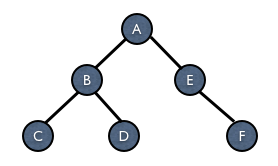  
![这里写图片描述][70]

前序遍历 ABCDEF  
中序遍历 CBDAEF  
后序遍历 CDBFEA  
已知二叉树的前序遍历和中序遍历，如何得到它的后序遍历  
其实，只要知道其中任意两种遍历的顺序，我们就可以推断出剩下的一种遍历方式的顺序，这里我们只是以：知道前序遍历和中序遍历，推断后序遍历作为例子，其他组合方式原理是一样的。要完成这个任务，我们首先要利用以下几个特性：  
特性A，对于前序遍历，第一个肯定是根节点；  
特性B，对于后序遍历，最后一个肯定是根节点；  
特性C，利用前序或后序遍历，确定根节点，在中序遍历中，根节点的两边就可以分出左子树和右子树；  
特性D，对左子树和右子树分别做前面3点的分析和拆分，相当于做递归，我们就可以重建出完整的二叉树；  
我们以一个例子做一下这个过程，假设：  
前序遍历的顺序是: CABGHEDF  
中序遍历的顺序是: GHBACDEF  
第一步，我们根据特性A，可以得知根节点是C，然后，根据特性C，我们知道左子树是：GHBA，右子树是：DEF。

>     C
>                       /     \
>                      GHBA   DEF

第二步，取出左子树，左子树的前序遍历是：ABGH，中序遍历是：GHBA，根据特性A和C，得出左子树的父节点是A，并且A没有右子树。

>     C
>                       /     \
>                     A         DEF
>                     /
>                   GBH

第三步，使用同样的方法，前序是BGH，中序是GHB，得出父节点是B，G和H是左子树，没有右子树。之后根据GH和GH得出G为根，H为右节点

>     C
>                       /     \
>                    A         DEF
>                  /
>                B
>               /    
>             G  
>               \            
>               H

第四步，回到右子树，它的前序是EDF，中序是DEF，依然根据特性A和C，得出父节点是E，左右节点是D和F。

>     C
>                       /     \
>                    A          E
>                  /          /    \
>                 B          D      F
>               /    
>             G 
>               \
>               H

到此，我们得到了这棵完整的二叉树，因此，它的后序遍历就是：HGBADFEC。

[http_blog.csdn.net_droidphone]: http://blog.csdn.net/droidphone
[70]: /images/20220524/56d2c138911d4849a48453522304c07b.png