Dijkstra最短路径算法-蒲公英云

Dijkstra最短路径算法

Dijkstra算法的运算步骤可以看下图：

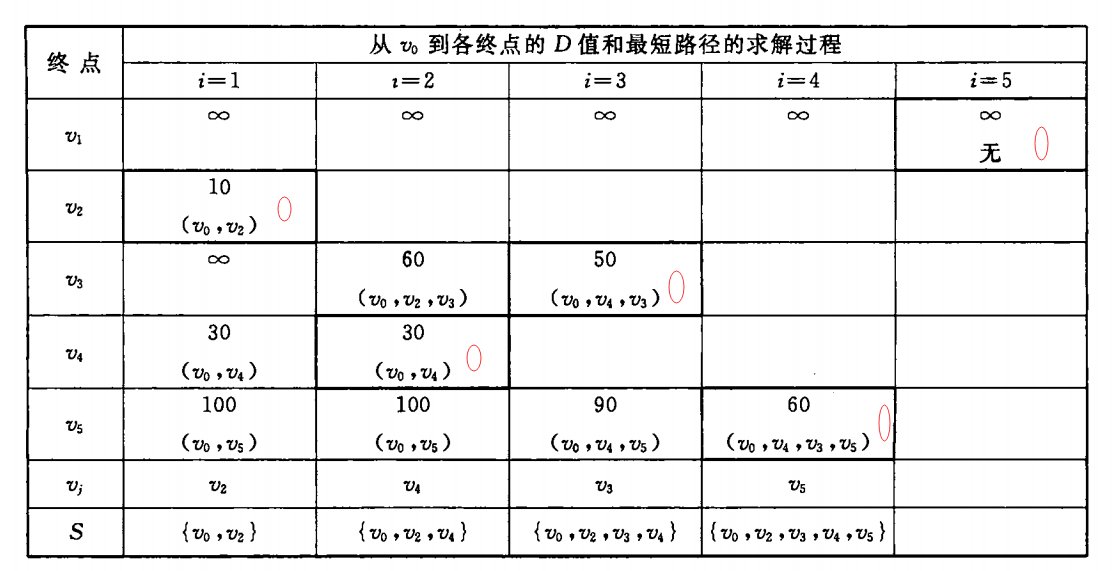
Center

即第一次选取最小的，第二次选取次小的，共需要支行 n-1次。

在上面的运算过程中需要注意几个问题：

1 已经得出结果的集合指 visit[n] 中 visit[x] = 1的那些元素，对于已经得出的结果的结点不需要再迭代。

用一个结构保存最短路径的距离，即 shortDistance[n]
用一个结构保存具体的路径是什么即 path[n]

如果一个图的邻接矩阵是 G[n][n] ，则最后的最短路径结果可以保存在 G[n][n] 的相应单元中，但这样就使 G[n][n] 发生了变化。

下面是一个具体的实现，思路还是比较明确的：

//算法要对照图进行理解
/*
    输入：
    G[][] 是图的邻接矩阵;
    v: 算法求 v 到其它结点的最短距离及路径
    paths: 存放求得的最短路径，在方法中进行设置
    输出：
    shortDistances: v到其它各点的最短路径距离
*/
public static double[] dijkstra(double G[][], int v, ArrayList<Integer>[] paths) {
    int n = G.length; //图的结点个数
    boolean[] visited = new boolean[n]; //是否到此结点已经求出最短路径 true 表示已经求出
    double[] shortDistances = new double[n]; //存放到各点的最短路径
    for(int i = 0; i < n; i++) {
        shortDistances[i] = G[v][i];
        paths[i] = new ArrayList<Integer>();
        paths[i].add(v);paths[i].add(i);
    }
    visited[v] = true;
    //需要 n-1 次循环
    for(int count = 0; count < n-1; count++) {
        double minD = Double.MAX_VALUE;
        int k = -1;
        //先求得本次循环的最短路径
        for(int i = 0; i < n; i++) {
            if(visited[i] == false && shortDistances[i] < minD) {
                minD = shortDistances[i];
                k = i;
            }
        }
        visited[k] = true;
        //修改其它结点
        for(int i = 0; i < n; i++) {
            if(visited[i] == false && shortDistances[i] > shortDistances[k] + G[k][i]) {
                shortDistances[i] = shortDistances[k] + G[k][i];
                paths[i] = new ArrayList<Integer>(paths[k]);
                paths[i].add(i);
            }
        }
    }
    return shortDistances;
}
/*在上面的运算过程中需要注意几个问题：
1 已经得出结果的集合  指 visit[n] 中  visit[x] = 1的那些元素，对于已经得出的结果的结点不需要再迭代。
2. 用一个结构保存 最短路径的距离，即 shortDistance[n]
3. 用一个结构保存 具体的路径是什么  即 path[n]
*/