最短路径Dijkstra算法
最短路径Dijkstra算法
本文取自《数据结构与算法》(C语言版)(第三版),出版社是清华大学出版社。
本博文作为学习资料整理。附书的截图:

最短路径的Dijkstra算法的基本思想是:设S为最短路径已确定的顶点集,V-S是最短距离尚未确定的顶点集。初始时,将源点V0添加到顶点集S中,即S={V0}。在当前顶点集V-S中选择一个最短路径最小的顶点来扩充顶点集S,以保证算法按路径长度递增的次序产生各顶点的最短路径。
Dijkstra算法的步骤示意图如下:
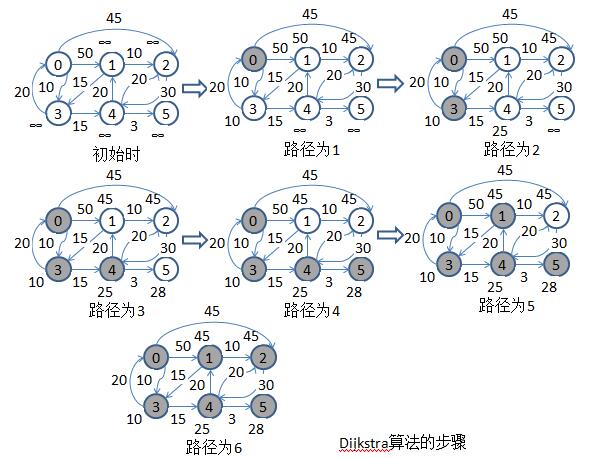
其程序如下:
#include<stdio.h>#include<stdlib.h>#include<string.h>#define MaxVertexNum 100const int INF=25500000;typedef struct node{int adjvex;int hostvex;struct node *nextrarc;int info;}EdgeNode;typedef struct vnode{char vexdate;int pos;EdgeNode *firstarc;}VertexNode;typedef VertexNode AdjList[MaxVertexNum];typedef struct{AdjList adjlist;int n,e;}ALGraph;int initGraph(ALGraph* aGraph);int mFind(char aChar, ALGraph* aGraph);int createHead(char aChar, ALGraph* aGraph);void addBody(char aChar, int aPos, ALGraph* aGraph, int weight);void showGraph(ALGraph* aGraph);EdgeNode* isEdge(VertexNode* start, VertexNode* end);void Dijkstra(ALGraph* aGraph, int v);void Dispath(int dist[], int path[], int s[], ALGraph* aGraph, int v);void privatePrintPath(ALGraph* aGraph, int path[], int curr, int v);int main(void){char a;int isFinish=0;int headPos=-1;char a1='@', a2='@', a3='@', a4='@', a5='@', a6='@', a7='@';ALGraph g_graph;initGraph(&g_graph);printf("Input arcs like this '(start,end:weight)',end with $\n");while(isFinish==0){while(1){a=getchar();if(a=='$'||a=='#'){if(a=='#')isFinish=1;break;}if(a==' '||a=='\n')continue;a1=a2;a2=a3;a3=a4;a4=a5;a5=a6;a6=a7;a7=a;if(a1=='('&&a3==','&&a5==':'&&a7==')'){if((headPos=mFind(a2,&g_graph))==-1)headPos=createHead(a2,&g_graph);addBody(a4,headPos,&g_graph,a6-48);}}}Dijkstra(&g_graph,2);return 0;}EdgeNode* isEdge(VertexNode* start, VertexNode* end){EdgeNode* temEdge=start->firstarc;while(temEdge!=NULL){if(temEdge->adjvex==end->pos)return temEdge;temEdge=temEdge->nextrarc;}return NULL;}void Dijkstra(ALGraph* aGraph, int v){int dist[MaxVertexNum], path[MaxVertexNum];int s[MaxVertexNum];int mindis,i,j,u;EdgeNode* temEdge;for(i=0; i<aGraph->n; i++){dist[i]=INF;s[i]=0;path[i]=-1;}temEdge=aGraph->adjlist[v].firstarc;while(temEdge!=NULL){dist[temEdge->adjvex]=temEdge->info;path[temEdge->adjvex]=v;temEdge=temEdge->nextrarc;}s[v]=1;path[v]=v;dist[v]=0;for(i=0; i<aGraph->n; i++){mindis=INF;for(j=0; j<aGraph->n; j++){if(s[j]==0&&dist[j]<mindis){u=j;mindis=dist[j];}}s[u]=1;for(j=0; j<aGraph->n; j++){if(s[j]==0){EdgeNode* temEdge=isEdge(&(aGraph->adjlist[u]), &(aGraph->adjlist[j]));if(temEdge!=NULL){if((dist[u]+temEdge->info)<dist[j]){dist[j]=dist[u]+temEdge->info;path[j]=u;}}}}}Dispath(dist,path,s,aGraph,v);}void Dispath(int dist[], int path[], int s[], ALGraph* aGraph, int v){int i;for(i=0; i<aGraph->n; i++){printf("%c->%c(distance is %d) \n%c", aGraph->adjlist[v].vexdate,aGraph->adjlist[i].vexdate,dist[i],aGraph->adjlist[v].vexdate);privatePrintPath(aGraph,path,i,v);printf("\n");}}void privatePrintPath(ALGraph* aGraph, int path[], int curr, int v){char temChar=aGraph->adjlist[curr].vexdate;int temPos=curr;if(curr!=v){privatePrintPath(aGraph,path,path[temPos],v);printf(" ->%c",temChar);}}void showGraph(ALGraph* aGraph){int i=0;for(i=0; i<aGraph->n; i++){EdgeNode* pos;printf(" %c->",aGraph->adjlist[i]);pos=aGraph->adjlist[i].firstarc;while(pos!=NULL){printf(" %d ",pos->adjvex);pos=pos->nextrarc;}printf("\n ");}}void addBody(char aChar, int aPos, ALGraph* aGraph, int weight){int inversePos;EdgeNode* node=(EdgeNode*) malloc(sizeof(EdgeNode));node->info=weight;if((node->adjvex=mFind(aChar,aGraph))==-1)node->adjvex=createHead(aChar,aGraph);node->hostvex=aPos;node->nextrarc=NULL;if(aGraph->adjlist[aPos].firstarc==NULL)aGraph->adjlist[aPos].firstarc=node;else{EdgeNode* tail=aGraph->adjlist[aPos].firstarc;while(tail->nextrarc!=NULL)tail=tail->nextrarc;tail->nextrarc=node;}aGraph->e++;inversePos=node->adjvex;node=(EdgeNode*) malloc(sizeof(EdgeNode));node->info=weight;node->hostvex=inversePos;node->adjvex=aPos;node->nextrarc=NULL;if(aGraph->adjlist[inversePos].firstarc==NULL)aGraph->adjlist[inversePos].firstarc=node;else{EdgeNode* tail=aGraph->adjlist[inversePos].firstarc;while(tail->nextrarc!=NULL)tail=tail->nextrarc;tail->nextrarc=node;}aGraph->e++;}int createHead(char aChar, ALGraph* aGraph){int currPos=aGraph->n;aGraph->adjlist[currPos].vexdate=aChar;aGraph->adjlist[currPos].pos=currPos;aGraph->n++;return currPos;}int mFind(char aChar, ALGraph* aGraph){int i=0;for(i=0; i<aGraph->n; i++){if(aChar==aGraph->adjlist[i].vexdate)return i;}return -1;}int initGraph(ALGraph* aGraph){int i=0;aGraph->e=0;aGraph->n=0;for(i=0; i<MaxVertexNum; i++){aGraph->adjlist[i].firstarc=NULL;}return 0;}
在VC2010中 C++控制台程序运行的结果:如下图所示:
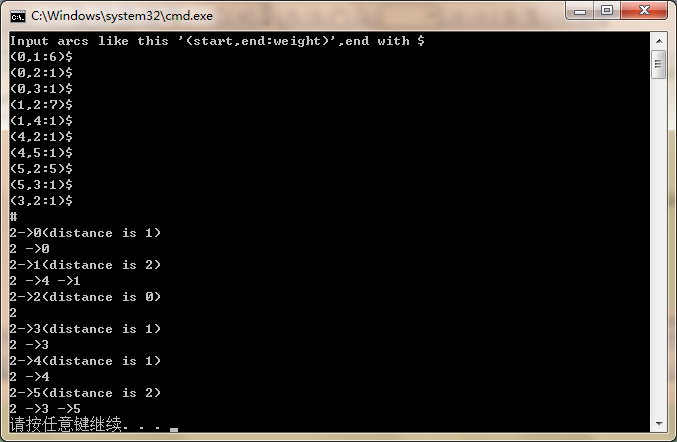






























还没有评论,来说两句吧...