python实现对语音信号的离散余弦变换（DCT）与离散余弦逆变换（IDCT）

忘是亡心i 2022-09-09 06:05 315阅读 0赞

### python实现对语音的离散余弦变换与离散余弦逆变换 ###

*  离散余弦变换
 *  离散余弦逆变换
 *  调包实现

# 离散余弦变换 #

离散余弦变换（DCT）信号谱分量丰富、能量集中，且不需要对语音相位进行估算等优点，在较低的运算复杂度下取得较好的语音增强效果。  
假设一余弦序列  
 x ( n ) = cos ⁡ ( 2 π f n f s ) ， 0 < = n < 1000 x(n)=\\cos(\\frac\{2\\pi fn\}\{ \{f\}\_\{s\}\})， 0<=n<1000 x(n)=cos(fs2πfn)，0<=n<1000  
其中f=50Hz， f s \{f\}\_\{s\} fs=1000Hz。  
则信号的离散余弦变换：  
 X ( k ) = 2 N ∑ n = 0 N − 1 C ( k ) x ( n ) cos ⁡ ( ( 2 n + 1 ) k π 2 N ) ， N = 0 , 1 , . . . N − 1 X(k) = \\sqrt\{\\frac\{2\}\{N\}\}\\sum\_\{n=0\}^\{N-1\}C(k)x(n)\\cos(\\frac\{(2n+1)k\\pi\}\{2N\})，N=0,1,...N-1 X(k)=N2n=0∑N−1C(k)x(n)cos(2N(2n\+1)kπ)，N=0,1,...N−1  
 C ( k ) C(k) C(k)是正交因子  
 C ( x ) = \{ 2 2 k=0 1 k=\[1,2,...N-1\] C(x)= \\begin\{cases\} \\frac\{\\sqrt\{2\}\}\{2\}& \\text\{k=0\}\\\\ 1& \\text\{k=\[1,2,...N-1\]\} \\end\{cases\} C(x)=\{ 221k=0k=\[1,2,...N-1\]

代码：

import numpy as np
    import cv2
    import matplotlib.pyplot as plt
    plt.rcParams['font.sans-serif']=['STSong']
    
    f = 50
    N = 1000
    fs = 1000
    n = np.array([i for i in range(N)])
    xn = np.cos(2 * np.pi * f * n / fs)
    
    # 离散余弦变换
    def dct(x):
        N = len(x)  # 获取信号长度
        X = np.zeros(N)  # 初始化
        ts = np.array([i for i in range(N)])
        C = np.ones(N)  # 初始化1
        C[0] = np.sqrt(2) / 2  # 将C[0]赋值
        for k in range(N):
            X[k] = np.sqrt(2 / N) * np.sum(C[k] * np.multiply(x, np.cos((2 * ts + 1) * k * np.pi / 2 / N)))
        return X
    # 函数调用
    s_dct = dct(xn)
    # 画出波形图
    plt.figure(figsize=(8, 4))
    plt.subplot(211)
    plt.plot(xn)
    plt.xlabel('样点')  # x轴样点
    plt.title('原信号', fontsize=12, color='black')  # 标题名称、字体大小、颜色
    plt.subplot(212)
    plt.plot(s_dct)
    plt.xlabel('样点')  # x轴样点
    plt.title('离散余弦变换', fontsize=12, color='black')  # 标题名称、字体大小、颜色
    plt.subplots_adjust(hspace=0.6)
    plt.show()

结果：  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5ZCD5Z2X5bCP6KW_55Oc_size_16_color_FFFFFF_t_70_g_se_x_16]

# 离散余弦逆变换 #

则DCT的逆变换为  
 x ( n ) = 2 N ∑ n = 0 N − 1 C ( k ) X ( k ) cos ⁡ ( ( 2 n + 1 ) k π 2 N ) ， N = 0 , 1 , . . . N − 1 x(n) = \\sqrt\{\\frac\{2\}\{N\}\}\\sum\_\{n=0\}^\{N-1\}C(k)X(k)\\cos(\\frac\{(2n+1)k\\pi\}\{2N\})，N=0,1,...N-1 x(n)=N2n=0∑N−1C(k)X(k)cos(2N(2n\+1)kπ)，N=0,1,...N−1  
代码：

# 离散余弦逆变换
    def idct(X):
        N = len(X)  # 获取信号长度
        x = np.zeros(N)  # 初始化
        ts = np.array([i for i in range(N)])
        C = np.ones(N)  # 初始化1
        C[0] = np.sqrt(2) / 2  # 将C[0]赋值
        for n in range(N):
            x[n] = np.sqrt(2 / N) * np.sum(np.multiply(np.multiply(C[ts], X[ts]), np.cos((2 * n + 1) * np.pi * ts / 2 / N)))
        return x
    # 函数调用
    s_idct = idct(ss_dct)
    
    plt.figure(figsize=(8, 4))
    plt.plot(s_idct)
    plt.xlabel('样点')  # x轴样点
    plt.title('离散余弦逆变换恢复', fontsize=12, color='black')  # 标题名称、字体大小、颜色
    plt.show()

结果：  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5ZCD5Z2X5bCP6KW_55Oc_size_16_color_FFFFFF_t_70_g_se_x_16 1]

# 调包实现 #

代码：

ds_dct = cv2.dct(xn)
    ds_idct = cv2.dct(ds_dct)
    # 画出波形图
    plt.figure(figsize=(8, 6))
    plt.subplot(311)
    plt.plot(xn)
    plt.xlabel('样点')  # x轴样点
    plt.title('原信号', fontsize=12, color='black')  # 标题名称、字体大小、颜色
    plt.subplot(312)
    plt.plot(ds_dct)
    plt.xlabel('样点')  # x轴样点
    plt.title('离散余弦变换', fontsize=12, color='black')  # 标题名称、字体大小、颜色
    plt.subplot(313)
    plt.plot(ds_idct)
    plt.xlabel('样点')  # x轴样点
    plt.title('离散余弦逆变换恢复', fontsize=12, color='black')  # 标题名称、字体大小、颜色
    plt.subplots_adjust(hspace=0.6)
    plt.show()

结果：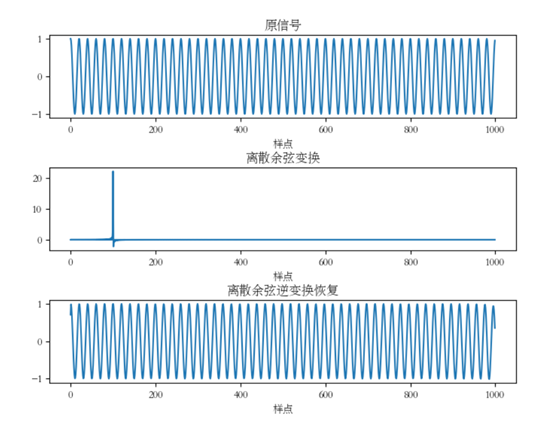  
![在这里插入图片描述][watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5ZCD5Z2X5bCP6KW_55Oc_size_16_color_FFFFFF_t_70_g_se_x_16 2]

[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5ZCD5Z2X5bCP6KW_55Oc_size_16_color_FFFFFF_t_70_g_se_x_16]: /images/20220829/5c1c45cc572d460f9db67fe6c8161935.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5ZCD5Z2X5bCP6KW_55Oc_size_16_color_FFFFFF_t_70_g_se_x_16 1]: /images/20220829/72e9b12e742c4d079a0b337cf69f5e86.png
[watermark_type_ZHJvaWRzYW5zZmFsbGJhY2s_shadow_50_text_Q1NETiBA5ZCD5Z2X5bCP6KW_55Oc_size_16_color_FFFFFF_t_70_g_se_x_16 2]: /images/20220829/7e3f79fd04924377917f54c6117623b2.png